Amortizacija
| (%i1) | load("FINMAT.mac"); |
1. zadatak
Oprema čija je cijena 400 000 kn ima životni vijek 5 godina i otpisnu vrijednost 100 000 kn. Napravite amortizacijsku tablicu
a) linearnom metodom amortizacije,
b) metodom sume znamenaka,
c) metodom konstantnog postotka.
| (%i3) |
C:400000$ S:100000$ |
a) dio
| (%i4) | LIN_amor(C,S,5); |
![(%o4) matrix(<BR>
["n", "Rk", "Dk", "Bk"],<BR>
[0, "-", "-", 400000.0],<BR>
[1, 60000.0, 60000.0, 340000.0],<BR>
[2, 60000.0, 120000.0, 280000.0],<BR>
[3, 60000.0, 180000.0, 220000.0],<BR>
[4, 60000.0, 240000.0, 160000.0],<BR>
[5, 60000.0, 300000.0, 100000.0]<BR>
)](amortizacija_htmlimg/amortizacija_1.png)
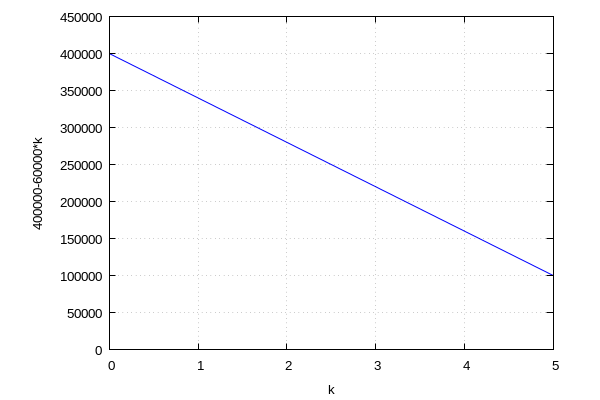
knjigovodstvena vrijednost kao funkcija vremena
| (%i5) | f1:LIN_fun_Bk(k,C,S,5); |
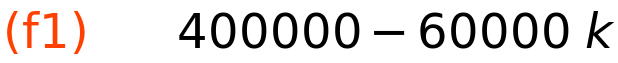
| (%i6) | wxplot2d(f1, [k,0,5], [y,0,450000],[gnuplot_postamble, "set grid;"])$ |

b) dio
| (%i7) | SZ_amor(C,S,5); |
![(%o7) matrix(<BR>
["n", "Rk", "Dk", "Bk"],<BR>
[0, "-", "-", 400000.0],<BR>
[1, 100000.0, 100000.0, 300000.0],<BR>
[2, 80000.0, 180000.0, 220000.0],<BR>
[3, 60000.0, 240000.0, 160000.0],<BR>
[4, 40000.0, 280000.0, 120000.0],<BR>
[5, 20000.0, 300000.0, 100000.0]<BR>
)](amortizacija_htmlimg/amortizacija_5.png)
knjigovodstvena vrijednost kao funkcija vremena
| (%i8) | f2:SZ_fun_Bk(k,C,S,5); |
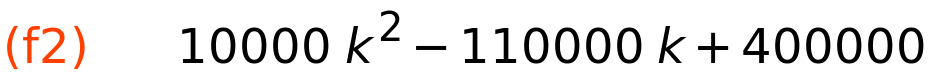
| (%i9) | wxplot2d(f2, [k,0,5], [y,0,450000],[gnuplot_postamble, "set grid;"])$ |

c) dio
| (%i10) | KS_amor(C,S,5); |
![(%o10) matrix(<BR>
["n", "Rk", "Dk", "Bk"],<BR>
[0, "-", "-", 400000.0],<BR>
[1, 96856.69, 96856.69, 303143.31],<BR>
[2, 73403.64, 170260.33, 229739.67],<BR>
[3, 55629.56, 225889.89, 174110.11],<BR>
[4, 42159.32, 268049.21, 131950.79],<BR>
[5, 31950.79, 300000.0, 100000.0]<BR>
)](amortizacija_htmlimg/amortizacija_9.png)
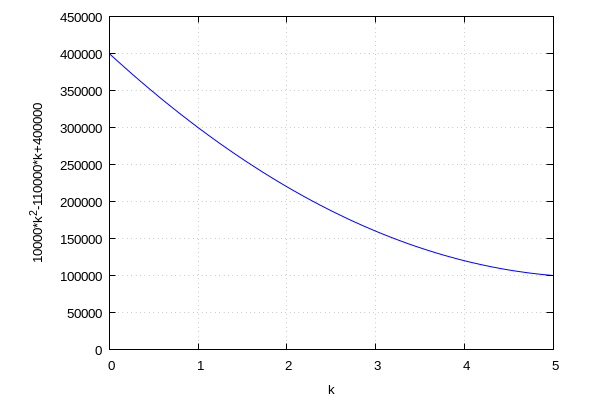
knjigovodstvena vrijednost kao funkcija vremena
| (%i11) | f3:KS_fun_Bk(k,C,S,5); |

| (%i12) | wxplot2d(f3, [k,0,5], [y,0,450000],[gnuplot_postamble, "set grid;"])$ |

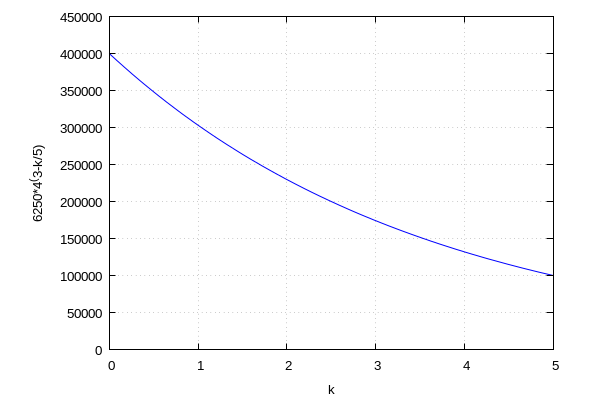
USPOREDBA VREMENSKIH METODA AMORTIZACIJE
| (%i13) |
wxplot2d([f1,f2,f3], [k,0,5], [y,0,450000],[gnuplot_postamble, "set grid;"], [legend,"linearna","suma znamenaka","konstantni postotak"], [color,red,blue,"#08e00c"])$ |

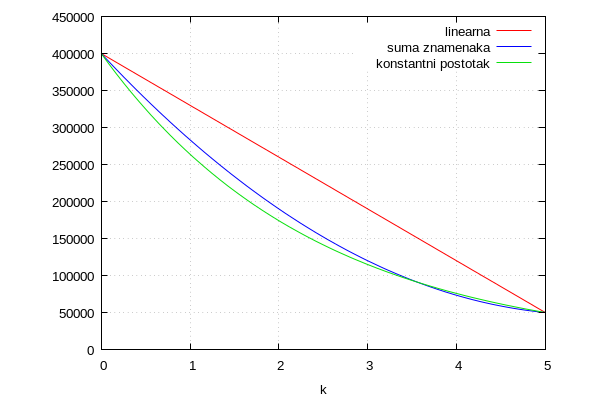
odnos grafova ovisi o početnim podacima
| (%i14) | S1:50000$ |
| (%i15) | g1:LIN_fun_Bk(k,C,S1,5); |
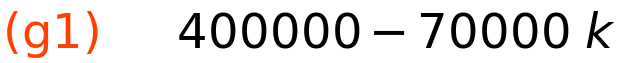
| (%i16) | g2:SZ_fun_Bk(k,C,S1,5); |
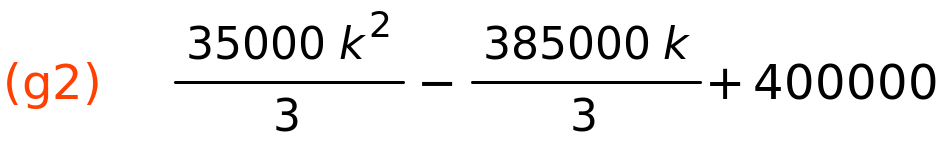
| (%i17) | g3:KS_fun_Bk(k,C,S1,5); |

| (%i18) |
wxplot2d([g1,g2,g3], [k,0,5], [y,0,450000],[gnuplot_postamble, "set grid;"], [legend,"linearna","suma znamenaka","konstantni postotak"], [color,red,blue,"#08e00c"])$ |

| (%i21) |
P:[4000,3500,2900,2600]$ C:60000$ S:8000$ |
| (%i22) | tablica:FUN_amor(P,C,S); |
![(tablica) matrix(<BR>
["n", "pk", "Rk", "Dk", "Bk"],<BR>
[0, "-", "-", "-", 60000.0],<BR>
[1, 4000, 16000.0, 16000.0, 44000.0],<BR>
[2, 3500, 14000.0, 30000.0, 30000.0],<BR>
[3, 2900, 11600.0, 41600.0, 18400.0],<BR>
[4, 2600, 10400.0, 52000.0, 8000.0]<BR>
)](amortizacija_htmlimg/amortizacija_20.png)
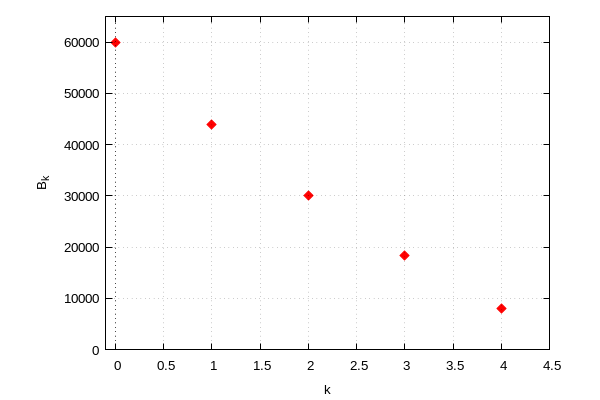
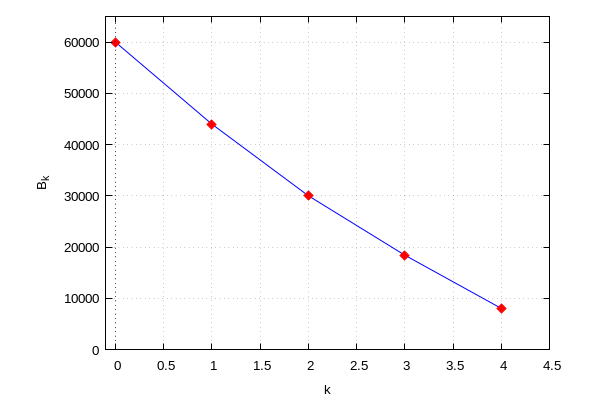
Grafički prikaz knjigovodstvene vrijednosti
| (%i23) | Bk:transpose(tablica)[5]; |
![(Bk) ["Bk",60000.0,44000.0,30000.0,18400.0,8000.0]](amortizacija_htmlimg/amortizacija_21.png)
| (%i24) | Bk:rest(Bk); |
![(Bk) [60000.0,44000.0,30000.0,18400.0,8000.0]](amortizacija_htmlimg/amortizacija_22.png)
| (%i25) | tocke:makelist([i−1,Bk[i]],i,1,5); |
![(tocke) [[0,60000.0],[1,44000.0],[2,30000.0],[3,18400.0],[4,8000.0]]](amortizacija_htmlimg/amortizacija_23.png)
| (%i26) |
wxplot2d([discrete, tocke], [x,−0.1,4.5], [y,0,65000], [grid2d,true], [style, points], [color, red], [point_type, diamond], [xlabel, "k"], [ylabel, "B_k"])$ |

| (%i27) |
wxplot2d([[discrete, tocke],[discrete,tocke]], [x,−0.1,4.5], [y,0,65000], [grid2d,true], [style, lines,points], [color, blue,red], [point_type, diamond], [xlabel, "k"], [ylabel, "B_k"],[legend,false])$ |

3. zadatak
Stroj vrijednosti 190 000 kn životnog vijeka pet godina na kraju radnog vijeka ima otpisnu vrijednost 40 000 kn. Izradite amortizacijsku tablicu ako se u prve dvije godine koristi linearna metoda amortizacije, a u preostale tri godine metoda konstantnog postotka, pri čemu je odnos otpisanih vrijednosti kod navedenih metoda 3:2 u korist linearne metode.
| (%i28) | otpis:190000−40000; |
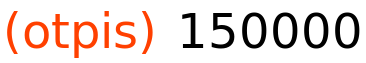
podaci za linearnu metodu
| (%i30) |
C1:190000; S1:C1−3/5·otpis; |
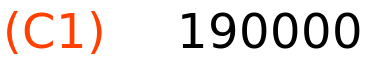
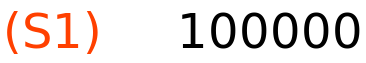
podaci za metodu konstantnog postotka
| (%i32) |
C2:S1; S2:40000; |
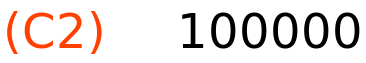

tablica za prve dvije godine
| (%i33) | LIN_amor(C1,S1,2); |
![(%o33) matrix(<BR>
["n", "Rk", "Dk", "Bk"],<BR>
[0, "-", "-", 190000.0],<BR>
[1, 45000.0, 45000.0, 145000.0],<BR>
[2, 45000.0, 90000.0, 100000.0]<BR>
)](amortizacija_htmlimg/amortizacija_33.png)
tablica za posljednje tri godine
| (%i34) | KS_amor(C2,S2,3), AMOR_Dk:90000; |
![(%o34) matrix(<BR>
["n", "Rk", "Dk", "Bk"],<BR>
[0, "-", 90000, 100000.0],<BR>
[1, 26319.37, 116319.37, 73680.63],<BR>
[2, 19392.28, 135711.65, 54288.35],<BR>
[3, 14288.35, 150000.0, 40000.0]<BR>
)](amortizacija_htmlimg/amortizacija_34.png)
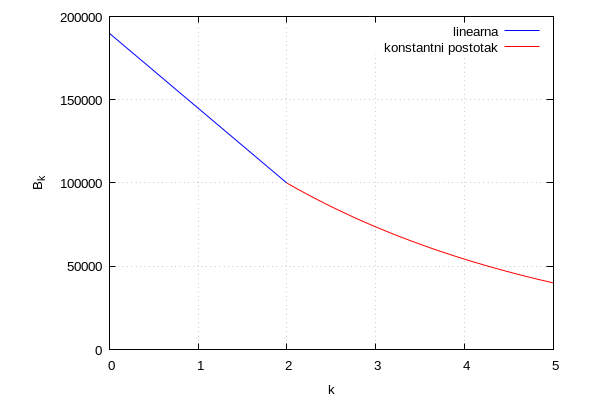
grafički prikaz knjigovodstvene vrijednosti
| (%i35) | f1:LIN_fun_Bk(k,C1,S1,2); |
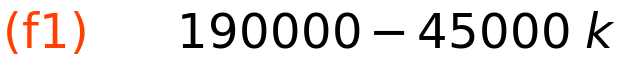
| (%i36) | f2:KS_fun_Bk(k−2,C2,S2,3); |
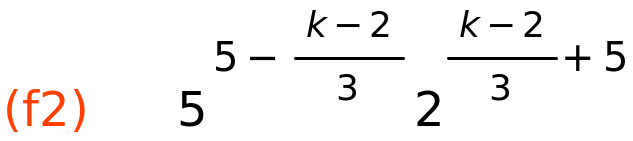
| (%i37) |
wxplot2d([if k<2 then f1,if k>2 then f2],[k,0,5],[y,0,200000], [grid2d,true],[legend,"linearna","konstantni postotak"], [ylabel,"B_k"])$ |


4. zadatak
Uređaj čija je nabavna vrijednost 200 000 kn ima životni vijek 8 godina. Na kraju radnog vijeka neće imati vrijednost, nego će trebati platiti 20 000 kn za njegovu demontažu i zbrinjavanje. Izračunajte amortizacijsku kvotu za amortizaciju linearnom metodom te odredite akumuliranu amortizaciju na kraju pete godine.
| (%i39) |
C:200000$ S:−20000$ |
Amortizacijska kvota
| (%i40) | R:(C−S)/8; |
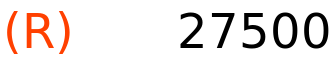
Akumulirana amortizacija na kraju pete godine
| (%i41) | 5·R; |
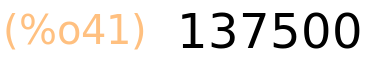
grafički prikaz knjigovodstvene vrijednosti
| (%i42) | f4:LIN_fun_Bk(k,C,S,8); |
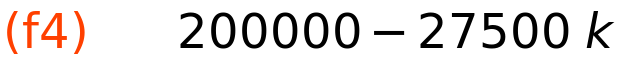
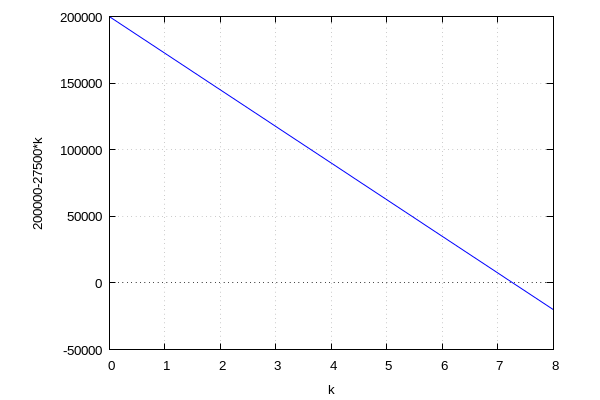
| (%i43) | wxplot2d(f4, [k,0,8], [grid2d,true])$ |

5. zadatak
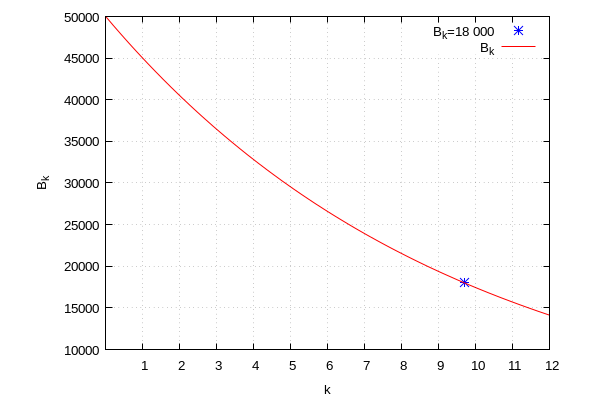
Oprema vrijedna 50 000 kn amortizira se metodom konstantnog postotka uz 10% godišnje. Nakon koliko će vremena vrijednost opreme biti manja od 18 000 kn?
| (%i46) |
C:50000$ Bk:18000$ d:10$ |
1. način: rješavanjem eksponencijalne jednadžbe
| (%i47) | solve_exp(C,1−d/100,Bk),FIN_dec:5; |
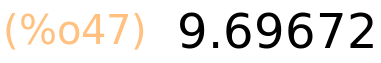
2. način: preko amortizacijske tablice
| (%i48) | KS_amor_dk(C,d,20); |
![(%o48) matrix(<BR>
["n", "Rk", "Dk", "Bk"],<BR>
[0, "-", "-", 50000.0],<BR>
[1, 5000.0, 5000.0, 45000.0],<BR>
[2, 4500.0, 9500.0, 40500.0],<BR>
[3, 4050.0, 13550.0, 36450.0],<BR>
[4, 3645.0, 17195.0, 32805.0],<BR>
[5, 3280.5, 20475.5, 29524.5],<BR>
[6, 2952.45, 23427.95, 26572.05],<BR>
[7, 2657.2, 26085.15, 23914.85],<BR>
[8, 2391.48, 28476.63, 21523.37],<BR>
[9, 2152.34, 30628.97, 19371.03],<BR>
[10, 1937.1, 32566.07, 17433.93],<BR>
[11, 1743.39, 34309.46, 15690.54],<BR>
[12, 1569.05, 35878.51, 14121.49],<BR>
[13, 1412.15, 37290.66, 12709.34],<BR>
[14, 1270.93, 38561.59, 11438.41],<BR>
[15, 1143.84, 39705.43, 10294.57],<BR>
[16, 1029.46, 40734.89, 9265.11],<BR>
[17, 926.51, 41661.4, 8338.6],<BR>
[18, 833.86, 42495.26, 7504.74],<BR>
[19, 750.47, 43245.73, 6754.27],<BR>
[20, 675.43, 43921.16, 6078.84]<BR>
)](amortizacija_htmlimg/amortizacija_46.png)
Iz oba načina rješavanja zaključujemo da će nakon 10 godina vrijednost opreme biti manja od 18 000 kn.
| (%i49) |
wxplot2d([[discrete,[[9.7,18000]]],C·(1−d/100)^k], [k,0,12], [style,points,lines],[point_type,asterisk], [grid2d,true],[xtics,1,1,12],[ylabel,"B_k"], [legend,"B_k=18 000","B_k"])$ |