Funkcije više varijabli - primjene u ekonomiji
| (%i1) | load(draw)$ |
1 zadatak
Dane su cijene dvaju dobara u ovisnosti o količinama proizvodnje p1=15-Q1 i p2=10-Q2, te funkcija troškova T(Q1,Q2)=5*Q1+4*Q2+5.
Pronađite optimalnu kombinaciju proizvodnje tako da dobit bude maksimalna. Koliko iznosi maksimalna dobit?
1.1 rješenje
prihod
| (%i3) |
P(Q1,Q2):=expand((15-Q1)*Q1+(10-Q2)*Q2)$ P(Q1,Q2); |
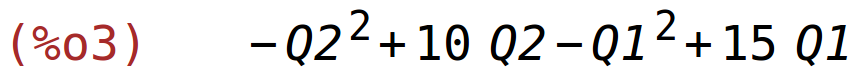
dobit
| (%i5) |
D(Q1,Q2):=P(Q1,Q2)-(5*Q1+4*Q2+5)$ D(Q1,Q2); |
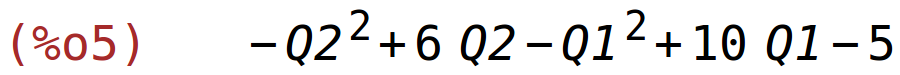
parcijalne derivacije
| (%i6) | D1:diff(D(Q1,Q2),Q1); |
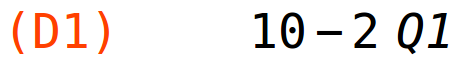
| (%i7) | D2:diff(D(Q1,Q2),Q2); |

stacionarna točka: (5,3)
| (%i8) | solve([D1=0,D2=0],[Q1,Q2]); |
![(%o8) [[Q1=5,Q2=3]]](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_4.png)
Maksimalna dobit se postiže za Q1=5 i Q2=3 te iznosi 29 novčanih jedinica.
| (%i9) | hessian(D(Q1,Q2),[Q1,Q2]); |
![(%o9) matrix(<BR>
[-2, 0],<BR>
[0, -2]<BR>
)](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_5.png)
| (%i10) | D(5,3); |

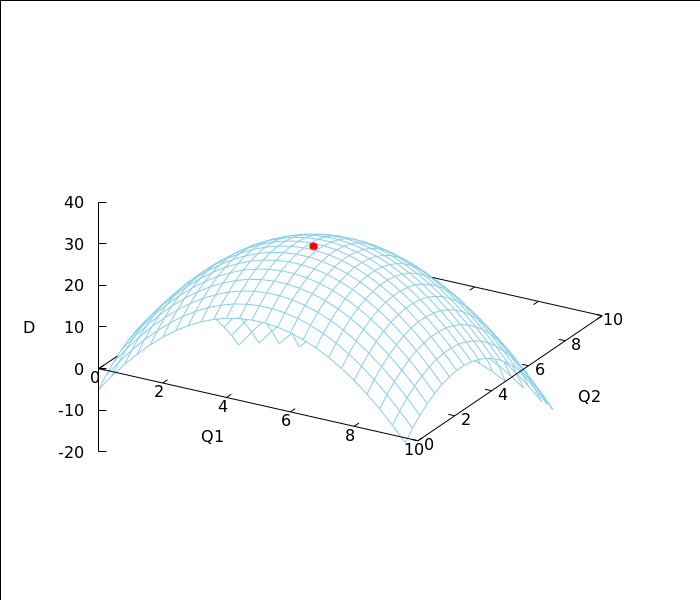
1.2 graf funkcije dobiti s istaknutom crvenom točkom maksimuma (5,3,29)
| (%i11) |
wxdraw3d(xu_grid=25,yv_grid=25,surface_hide=true,zrange=[-20,40],color=skyblue, xlabel="Q1",ylabel="Q2",zlabel="D", explicit(D(Q1,Q2), Q1,0,10, Q2,0,10), color=red,point_type=7,point_size=1.2,points([[5,3,29]]), user_preamble= "set xyplane at 0"),wxplot_size=[700,600]; |
2 zadatak
Zadana je funkcija troškova T(Q1,Q2)=2*Q1^2+Q1*Q2+Q2^2 u ovisnosti o količinama proizvodnje za dva proizvoda.
Odredite uz koju kombinaciju proizvodnje su troškovi minimalni pri čemu je ukupna proizvodnja jednaka 20 proizvoda.
2.1 rješenje
| (%i12) | T(Q1,Q2):=2*Q1^2+Q1*Q2+Q2^2; |
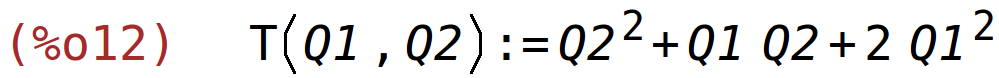
Uvrstimo uvjet Q1+Q2=20 u funkciju troškova
| (%i13) | fun:expand(T(Q1,20-Q1)); |
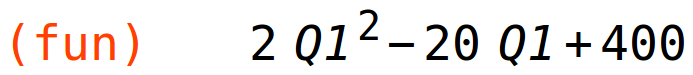
dobivamo funkciju jedne varijable čije ekstreme tražimo na standardni način
| (%i14) | der:diff(fun,Q1); |
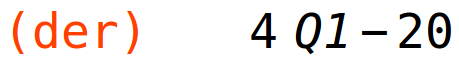
stacionarna točka: 5
| (%i15) | solve(der=0,Q1); |
![(%o15) [Q1=5]](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_13.png)
U točki 5 je minimum
| (%i16) | diff(fun,Q1,2); |
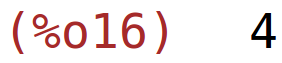
Uvrstimo Q1=5 u uvjet Q1+Q2=20 pa dobivamo Q2=15.
Dakle, na razini proizvodnje od 20 proizvoda minimalni troškovi se postižu za Q1=5, Q2=15 i jednaki su 350 novčanih jedinica.
| (%i17) | T(5,15); |
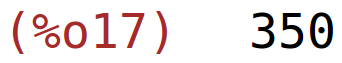
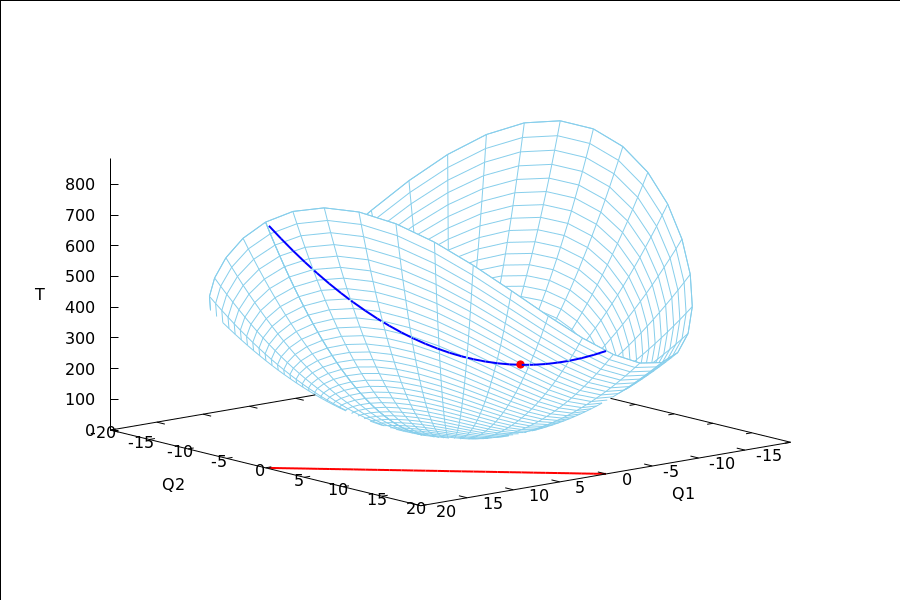
2.2 slika
→ Graf funkcije troškova je svijetloplava ploha.
→ Uvjet Q1+Q2=20 zapravo znači da se u domeni šećemo po crvenom pravcu.
→ Prilikom šetnje po crvenom pravcu, na plohi se šećemo samo po plavoj krivulji.
→ Vidimo da na plavoj krivulji na plohi postoji najniža crvena točka.
| (%i18) |
wxdraw3d(xu_grid=40,yv_grid=40,surface_hide=true,view=[70,140],color=skyblue, xlabel="Q1",ylabel="Q2",zlabel="T", parametric_surface(u*cos(v),u*sin(v),2*u^2*cos(v)^2+u^2*cos(v)*sin(v)+u^2*sin(v)^2, u,0,20, v,0,2*%pi), color=blue,line_width=2,parametric(u,20-u,T(u,20-u),u,0,19.8), color=red,point_type=7,point_size=1.2,points([[5,15,350]]), parametric(u,20-u,0,u,0,19.8), user_preamble= "set xyplane at 0"),wxplot_size=[900,600]; |

3 zadatak
Zadana je funkcija ponude s1(p1,p2)=10*p1^(1/2)-2*p2^2 gdje su p1 i p2 cijene po jedinici pojedinog proizvoda.
a) Za koliko se približno promijeni ponuda kada cijenu p1 na nivou p1=1, p2=2 povećamo za 0.02?
b) Za koliko se približno promijeni ponuda kada cijenu p2 na nivou p1=1, p2=2 smanjimo za 0.01?
c) Za koliko se približno promijeni ponuda kada istovremeno napravimo promjene iz a) i b) dijela zadatka?
3.1 rješenje
| (%i19) | s1(p1,p2):=10*sqrt(p1)-2*p2^2; |
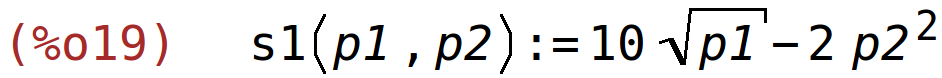
parcijalne derivacije
| (%i20) | der1:diff(s1(p1,p2),p1); |
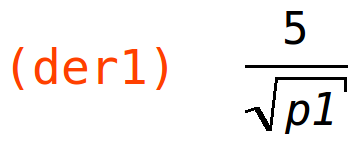
| (%i21) | der2:diff(s1(p1,p2),p2); |

a) dio: odredit ćemo stvarnu promjenu i približnu promjenu pomoću parcijalne derivacije po varijabli p1
stvarna promjena
| (%i22) | s1(1.02,2)-s1(1,2); |
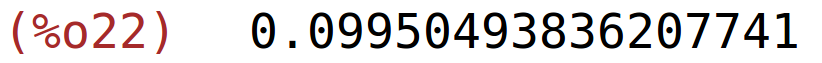
približna promjena
| (%i23) | pr1:subst([p1=1,p2=2],der1)*0.02; |

b) dio: odredit ćemo stvarnu promjenu i približnu promjenu pomoću parcijalne derivacije po varijabli p2
stvarna promjena
| (%i24) | s1(1,1.99)-s1(1,2); |
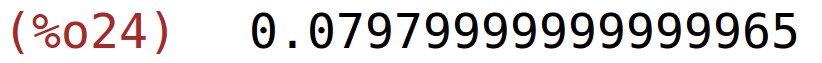
približna promjena
| (%i25) | pr2:subst([p1=1,p2=2],der2)*(-0.01); |

c) dio: odredit ćemo stvarnu promjenu i približnu promjenu pomoću diferencijala
stvarna promjena
| (%i26) | s1(1.02,1.99)-s1(1,2); |
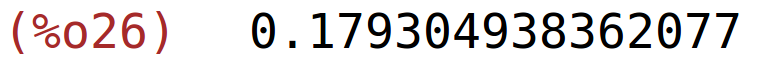
približna promjena
| (%i27) | pr1+pr2; |
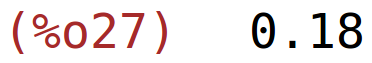
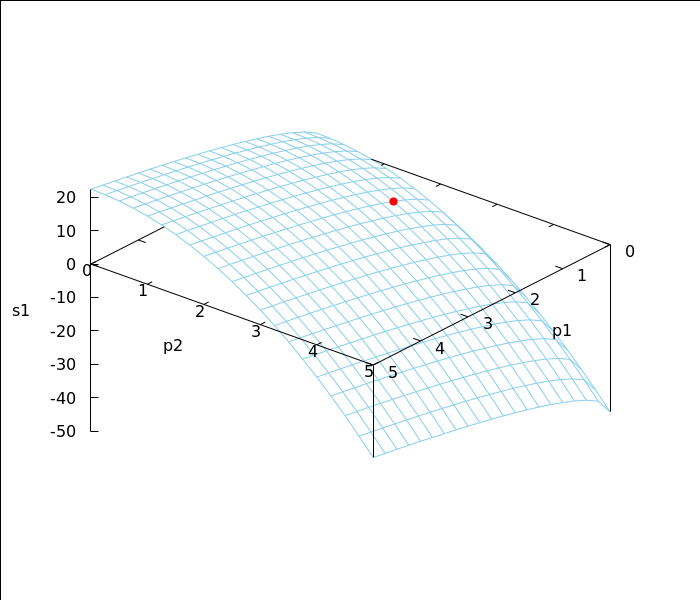
3.2 graf zadane funkcije ponude
Na plohi je istaknuta točka u kojoj smo računali promjene funkcije.
| (%i28) |
wxdraw3d(xu_grid=20,yv_grid=20,surface_hide=true,view=[57,130],color=skyblue, xlabel="p1",ylabel="p2",zlabel="s1", explicit(s1(p1,p2), p1,0,5, p2,0,5), color=red,point_type=7,point_size=1.2,points([[1,2,s1(1,2)]]), user_preamble= "set xyplane at 0"),wxplot_size=[700,600]; |


4 zadatak
Zadana je funkcija f(x,y)=(x+1)*e^(y^(1/2)). Izračunajte koeficijente parcijalnih elastičnosti
funkcije f na nivou x=2, y=1 i interpretirajte rezultate.
4.1 rješenje
| (%i29) | f(x,y):=(x+1)*%e^sqrt(y); |
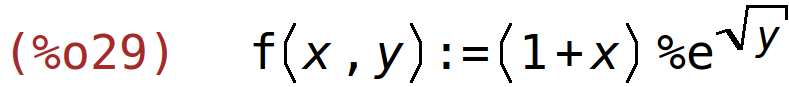
parcijalne derivacije
| (%i30) | fx:diff(f(x,y),x); |

| (%i31) | fy:diff(f(x,y),y); |
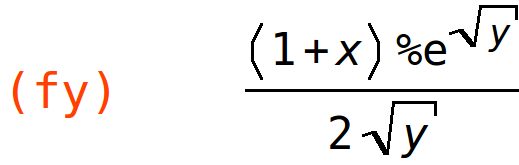
parcijalne elastičnosti
| (%i32) | elx:x/f(x,y)*fx; |

| (%i33) | ely:y/f(x,y)*fy; |

koeficijenti na nivou x=2, y=1
Ako na nivou (2,1) varijablu x povećamo za 1%, vrijednost funkcije f se poveća za 0.66%.
| (%i34) | subst([x=2,y=1],elx); |

Ako na nivou (2,1) varijablu y povećamo za 1%, vrijednost funkcije f se poveća za 0.5%.
| (%i35) | subst([x=2,y=1],ely); |

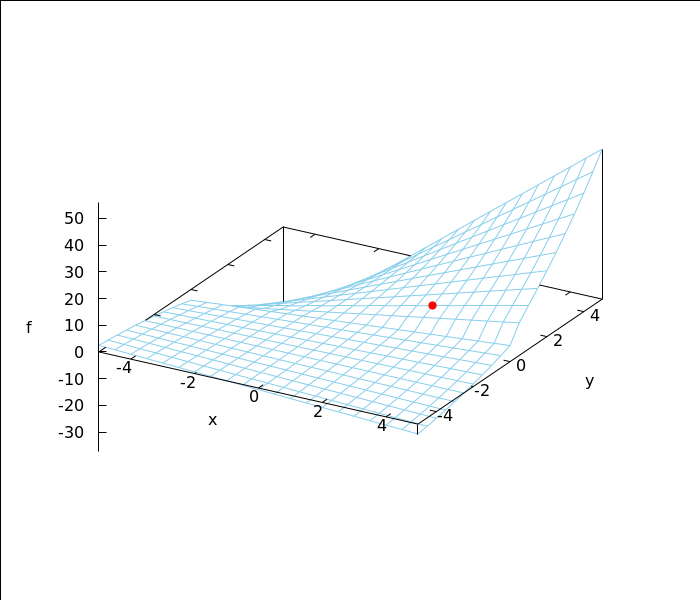
4.2 graf funkcije f
Na plohi je istaknuta točka u kojoj smo računali parcijalne elastičnosti funkcije f.
| (%i36) |
wxdraw3d(xu_grid=20,yv_grid=20,surface_hide=true,color=skyblue, xlabel="x",ylabel="y",zlabel="f", explicit(f(x,y), x,-5,5, y,-5,5), color=red,point_type=7,point_size=1.2,points([[2,1,f(2,1)]]), user_preamble= "set xyplane at 0"),wxplot_size=[700,600]; |


5 zadatak
Izračunajte koeficijente parcijalnih elastičnosti funkcije g(x,y)=(x-y^2)^(1/2) na nivou
x=25, y=3 i interpretirajte rezultate.
5.1 rješenje
| (%i37) | g(x,y):=sqrt(x-y^2); |
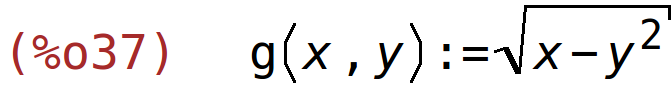
parcijalne derivacije
| (%i38) | gx:diff(g(x,y),x); |
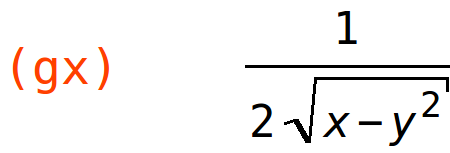
| (%i39) | gy:diff(g(x,y),y); |
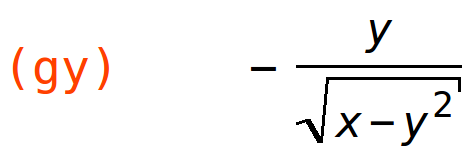
parcijalne elastičnosti
| (%i40) | elx:x/g(x,y)*gx; |
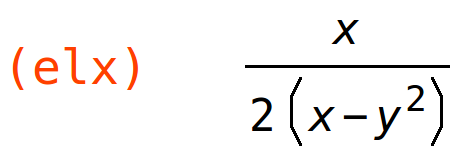
| (%i41) | ely:y/g(x,y)*gy; |
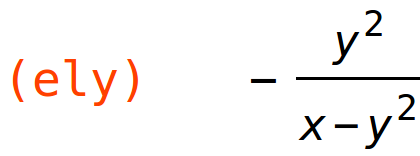
koeficijenti na nivou x=25, y=3
Ako na nivou (25,3) varijablu x povećamo za 1%, vrijednost funkcije g se poveća za 0.78125%.
| (%i42) | subst([x=25,y=3],elx); |

| (%i43) | %,numer; |

Ako na nivou (25,3) varijablu y povećamo za 1%, vrijednost funkcije g se smanji za 0.5625%.
| (%i44) | subst([x=25,y=3],ely); |

| (%i45) | %,numer; |
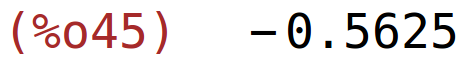
5.2 graf funkcije g
Na plohi je istaknuta točka u kojoj smo računali parcijalne elastičnosti funkcije g.
| (%i46) |
wxdraw3d(xu_grid=25,yv_grid=25,surface_hide=true,view=[60,135],color=skyblue, xlabel="x",ylabel="y",zlabel="g", parametric_surface(u,sqrt(u)*(2*v-1),2*sqrt(u*v-u*v^2), u,0,50, v,0,1), color=red,point_type=7,point_size=1.2,points([[25,3,g(25,3)]]), user_preamble= "set xyplane at 0"),wxplot_size=[700,600]; |



6 zadatak
Dana je funkcija potražnje q2(p1,p2)=2*p1*(10-p2)^(1/2). Izračunajte i interpretirajte koeficijente
parcijalne i križne elastičnosti na nivou cijena p1=5, p2=1. Jesu li proizvodi komplementi ili supstituti?
6.1 rješenje
| (%i47) | q2(p1,p2):=2*p1*sqrt(10-p2); |
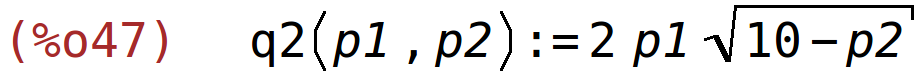
parcijalne derivacije
| (%i48) | der1:diff(q2(p1,p2),p1); |
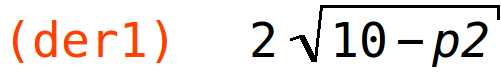
| (%i49) | der2:diff(q2(p1,p2),p2); |
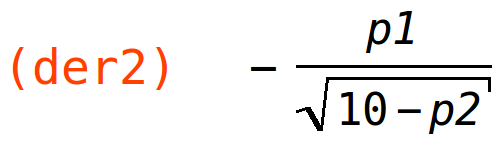
parcijalne elastičnosti
| (%i50) | el1:p1/q2(p1,p2)*der1; |
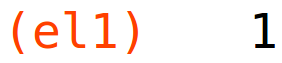
| (%i51) | el2:p2/q2(p1,p2)*der2; |
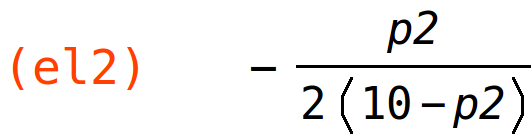
koeficijent parcijalne elastičnosti
Ako na nivou cijena p1=5, p2=1 cijenu p2 povećamo za 1%, potražnja za drugim proizvodom se smanji za 0.06%.
Drugi proizvod je stoga normalno dobro.
| (%i52) | subst([p1=5,p2=1],el2); |

| (%i53) | %,numer; |
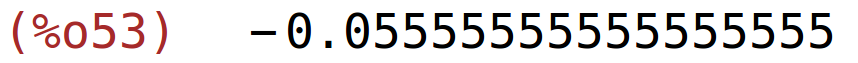
koeficijent križne elastičnosti
Ako na nivou cijena p1=5, p2=1 cijenu p1 povećamo za 1%, potražnja za drugim proizvodom se poveća za 1%.
Proizvodi su supstituti.
| (%i54) | subst([p1=5,p2=1],el1); |

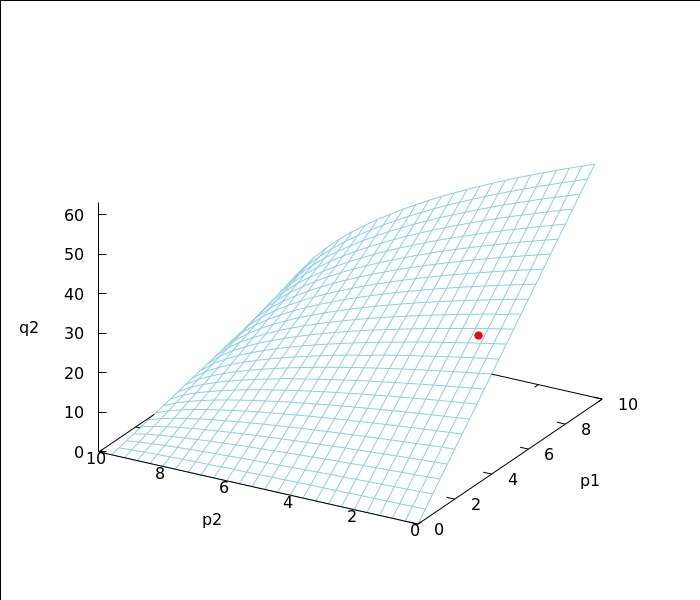
6.2 graf funkcije potražnje q2
Na plohi je istaknuta točka u kojoj smo računali parcijalne elastičnosti.
| (%i55) |
wxdraw3d(xu_grid=25,yv_grid=25,surface_hide=true,view=[60,300],color=skyblue, xlabel="p1",ylabel="p2",zlabel="q2", explicit(q2(p1,p2),p1,0,10, p2,0,10), color=red,point_type=7,point_size=1.2,points([[5,1,q2(5,1)+0.05]]), user_preamble= "set xyplane at 0"),wxplot_size=[700,600]; |


7 zadatak
Zadana je funkcija proizvodnje Q(L,K)=2*L^0.25*K^0.5 u ovisnosti o radu L i kapitalu K.
a) Odredite funkciju granične produktivnosti rada i interpretirajte rezultat na nivou L=10, K=5.
b) Odredite funkciju granične produktivnosti kapitala i interpretirajte rezultat na nivou L=10, K=5.
c) Provjerite da je Q homogena funkcija. Kakav tip prinosa određuje zadana funkcija proizvodnje?
d) Za koliko se promijeni količina proizvodnje ako rad i kapital povećamo za 10%?
e) Odredite jednadžbu izokvante L=L(K) na nivou proizvodnje Q=81.
7.1 rješenje
| (%i56) | Q(L,K):=2*L^0.25*K^0.5; |
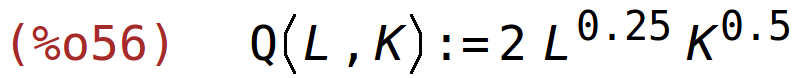
a) dio
Ako na nivou L=10, K=5 rad povećamo za jednu jedinicu, proizvodnja će se povećati za 0.2 jedinice.
| (%i57) | QL:diff(Q(L,K),L); |
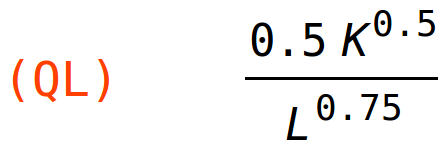
| (%i58) | subst([L=10,K=5],QL); |

b) dio
Ako na nivou L=10, K=5 kapital povećamo za jednu jedinicu, proizvodnja će se povećati za 0.8 jedinica.
| (%i59) | QK:diff(Q(L,K),K); |
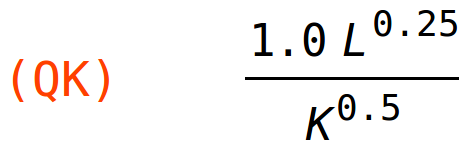
| (%i60) | subst([L=10,K=5],QK); |
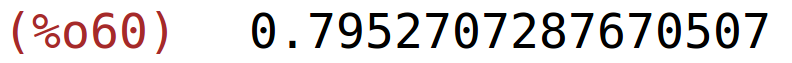
c) dio
Q je homogena funkcija sa stupnjem homogenosti 0.75.
Kako je stupanj homogenosti manji od 1, zadana funkcija proizvodnje ima padajuće prinose.
| (%i61) | assume(a>0,L>0,K>0); |
![(%o61) [a>0,L>0,K>0]](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_69.png)
| (%i62) | ratsimp(Q(a*L,a*K)/Q(L,K)); |
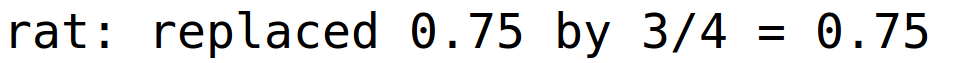
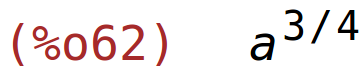
d) dio
Ako rad i kapital povećamo za 10%, proizvodnja se poveća za 7.41%.
| (%i63) | 1.1^0.75; |
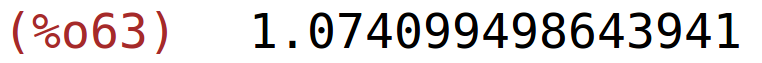
e) dio
| (%i64) | solve(Q(L,K)=81,L); |

![(%o64) [L=43046721/(16*K^2)]](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_74.png)
7.2 graf funkcije proizvodnje
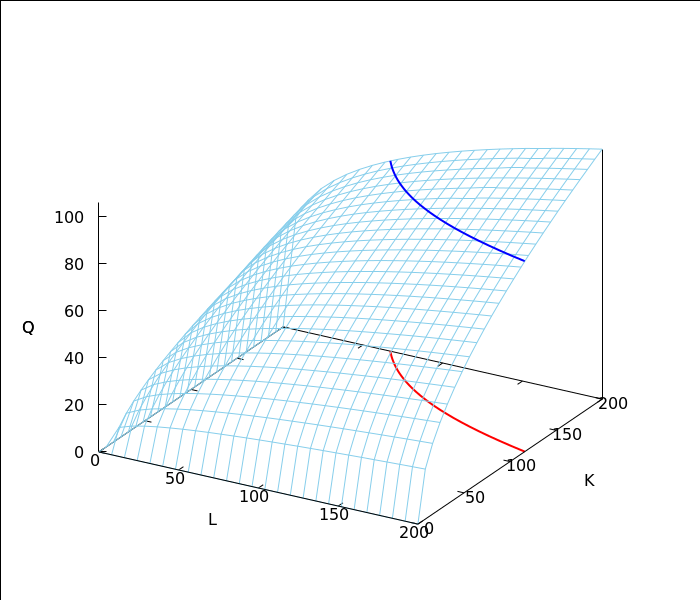
Na slici je prikazana i izokvanta (crvena krivulja) te pripadna plava krivulja na plohi na kojoj je proizvodnja jednaka 81.
| (%i65) |
wxdraw3d(xu_grid=25,yv_grid=25,surface_hide=false, xlabel="L",ylabel="K",zlabel="Q", color=red,line_width=2,parametric(43046721/(16*u^2),u,0,u,116,200), color=skyblue,line_width=1,explicit(Q(L,K),L,0,200, K,0,200), color=blue,line_width=2,parametric(43046721/(16*u^2),u,81.05,u,116,200), user_preamble= "set xyplane at 0"),wxplot_size=[700,600]; |


8 zadatak
Zadana je funkcija proizvodnje Q(L,K)=3*L^0.5*K u ovisnosti o radu L i kapitalu K.
a) Ako jedna jedinica rada košta 10 eura, jedna jedinica kapitala 15 eura, a poduzeće
ima na raspolaganju 20000 eura, nađite kombinaciju rada i kapitala za koju se uz
maksimalno iskorištenje budžeta ostvaruje maksimalna proizvodnja.
Koliko iznosi maksimalna proizvodnja?
b) Na istoj slici prikažite budžetsko ograničenje i izokvantu na nivou maksimalne proizvodnje.
Što vrijedi?
8.1 rješenje
| (%i66) | Q(L,K):=3*L^0.5*K; |
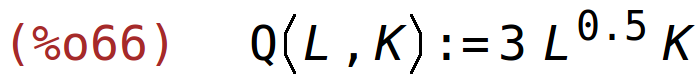
Iz uvjeta 10*L+15*K=20000 izrazimo jednu varijablu pomoću preostale i uvrstimo u funkciju Q.
| (%i67) | solve(10*L+15*K=20000,L); |
![(%o67) [L=-(3*K-4000)/2]](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_79.png)
Dobivamo funkciju jedne varijable čije ekstreme tražimo na standardni način.
| (%i68) | fun:Q(2000-3/2*K,K); |
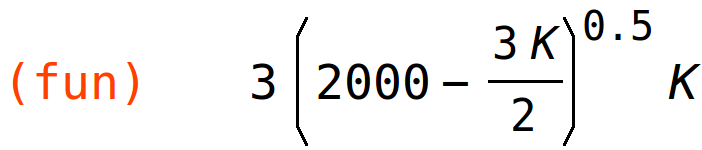
Stacionarna točka: K=8000/9
| (%i69) | der:ratsimp(diff(fun,K)); |

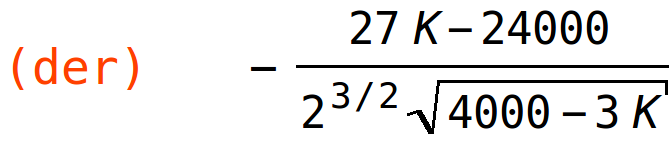
| (%i70) | solve(der=0,K); |
![(%o70) [K=8000/9]](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_83.png)
U K=8000/9 je lokalni maksimum
| (%i71) | der2:ratsimp(diff(fun,K,2)); |

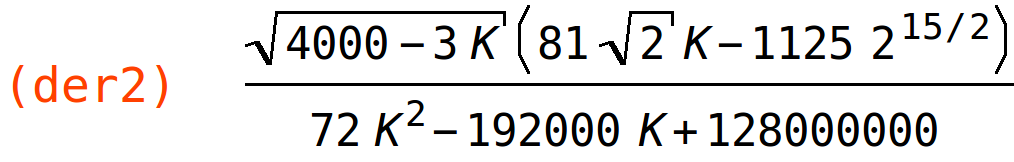
| (%i72) | subst(K=8000/9,der2),numer; |
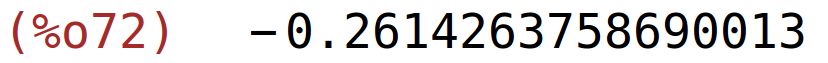
Uvrstimo K=8000/9 u uvjet 10*L+15*K=20000 pa dobivamo L=2000/3.
| (%i73) | solve(10*L+15*8000/9=20000,L); |
![(%o73) [L=2000/3]](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_87.png)
maksimalna proizvodnja
| (%i74) | mp:Q(2000/3,8000/9); |
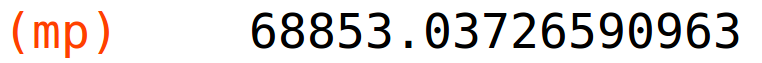
izokvanta na nivou maksimalne proizvodnje
| (%i75) | solve(Q(L,K)=mp,K); |
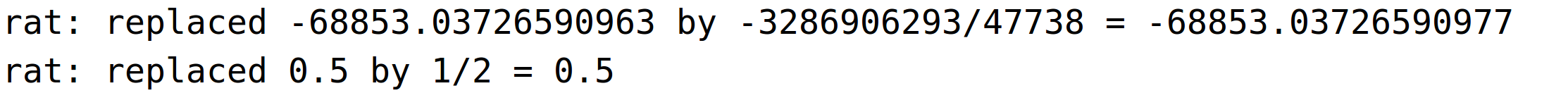
![(%o75) [K=1095635431/(47738*sqrt(L))]](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_90.png)
budžetsko ograničenje je tangenta na izokvantu na nivou maksimalne proizvodnje
| (%i76) |
wxdraw2d(grid=true,color=red,line_width=2,xlabel="L",ylabel="K", explicit(4000/3-2/3*L,L,0,2000),color=blue, explicit(1095635431/(47738*sqrt(L)),L,100,4000)); |

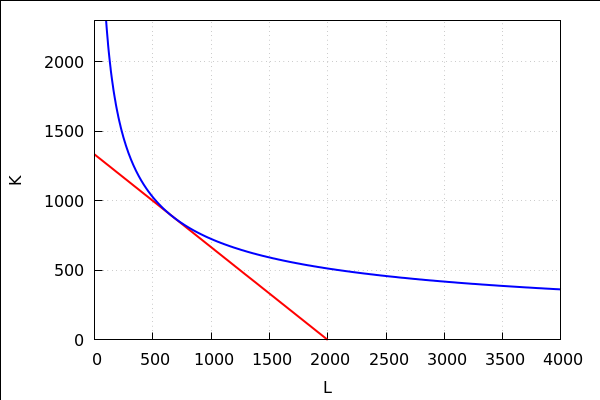

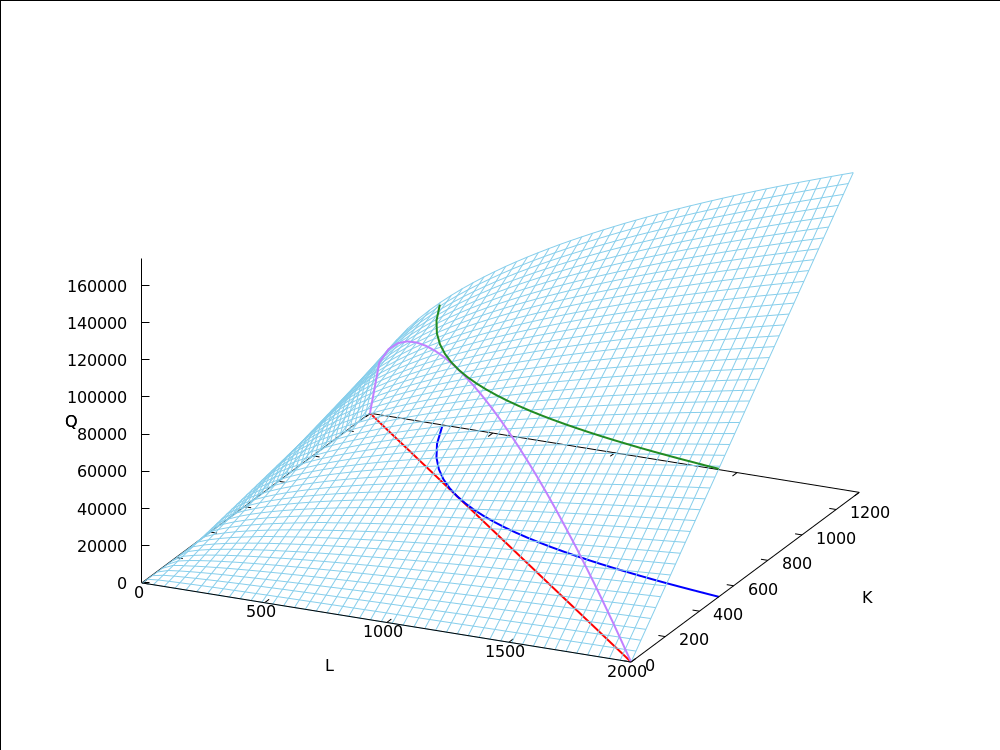
8.2 graf funkcije proizvodnje
→ crveni pravac je budžetsko ograničenje
→ kada se u domeni šećemo samo po crvenom pravcu, na plohi se zapravo šećemo po ljubičastoj krivulji
→ vidimo da na ljubičastoj krivulji postoji najviša točka
→ izokvanta u toj najvišoj točki na plohi (zelena krivulja) je izokvanta na nivou maksimalne proizvodnje uz zadano budžetsko ograničenje
→ plava krivulja je zapravo izokvanta spuštena u domenu i ona je tangencijalna na budžetsko ograničenje
| (%i77) |
wxdraw3d(xu_grid=45,yv_grid=45,surface_hide=false, xlabel="L",ylabel="K",zlabel="Q",view=[60,25], color=red,line_width=2,parametric(2000-3/2*u,u,0,u,0,4000/3), color=blue,line_width=2,parametric(u,68853.04/(3*u^0.5),0,u,300,2000), color=skyblue,line_width=1,explicit(Q(L,K),L,0,2000, K,0,1300), color=purple,line_width=2,parametric(2000-3/2*K,K,Q(2000-3/2*K,K),K,0,1335), color=forest_green,parametric(u,68853.04/(3*u^0.5),68853.04,u,320,2000), user_preamble= "set xyplane at 0"),wxplot_size=[1000,750]; |


9 zadatak
Neka je cijena jedinice rada 1 euro, jedinice kapitala 2 eura, a fiksni troškovi iznose 10 eura.
Funkcija proizvodnje u ovisnosti o radu L i kapitalu K dana je s Q(L,K)=0.5^0.5*L*K^0.5.
Na nivou proizvodnje Q=8 pronađite optimalnu kombinaciju rada i kapitala tako da troškovi budu
minimalni. Koliko iznose minimalni troškovi?
9.1 rješenje
funkcija proizvodnje
| (%i78) | Q(L,K):=sqrt(0.5)*L*K^0.5; |
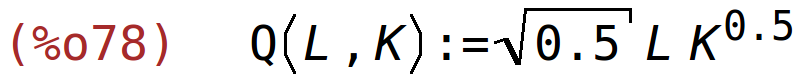
funkcija troškova
| (%i79) | T(L,K):=L+2*K+10; |
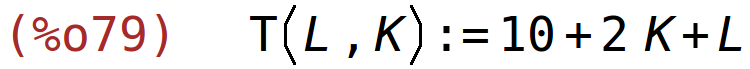
Tražimo ekstreme funkcije T uz uvjet Q(L,K)=8.
Izrazimo iz uvjeta varijablu L i uvrstimo u funkciju T.
| (%i80) | solve(Q(L,K)=8,L); |
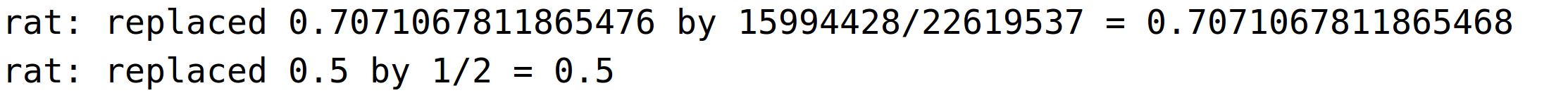
![(%o80) [L=45239074/(3998607*sqrt(K))]](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_100.png)
| (%i81) | fun:T(45239074/(3998607*sqrt(K)),K); |
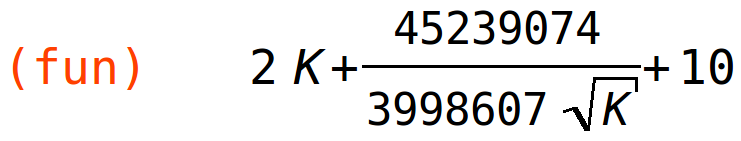
Dobivamo funkciju jedne varijable čije ekstreme tražimo na standardni način.
| (%i82) | der:diff(fun,K); |
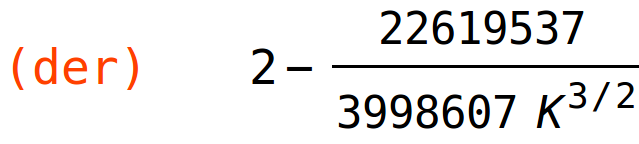
| (%i83) | solve(der=0,K),numer; |

![(%o83) [K=2]](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_104.png)
U stacionarnoj točki K=2 je zaista lokalni minimum.
Iz geometrijskih razloga je jasno da je to ujedno i globalni uvjetni minimum.
| (%i84) | der2:diff(fun,K,2); |
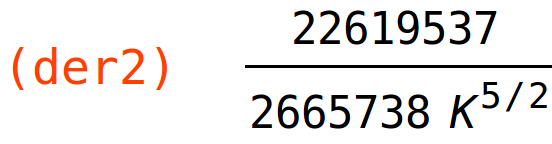
| (%i85) | subst(K=2,der2),numer; |
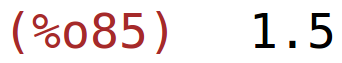
Uvrstimo K=2 u uvjet Q(L,K)=8 i dobivamo L=8.
| (%i86) | solve(Q(L,2)=8,L); |
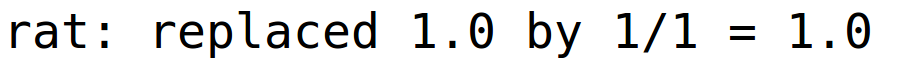
![(%o86) [L=8]](funkcije vise varijabli primjene_htmlimg/funkcije vise varijabli primjene_108.png)
Minimalni troškovi na nivou proizvodnje Q=8 se postižu za L=8, K=2 i iznose 22 eura.
| (%i87) | T(8,2); |

9.2 graf funkcije troškova
→ Uvjet Q(L,K)=8 je crvena krivulja u domeni.
→ Kada se u domeni šećemo po crvenoj krivulji, na plohi se šećemo po plavj krivulji.
→ Vidimo da postoji najniža točka na plavoj krivulji i pripadna crvena točka u domeni
u kojoj se postižu minimalni troškovi.
| (%i88) |
wxdraw3d(xu_grid=30,yv_grid=30,surface_hide=false, xlabel="L",ylabel="K",zlabel="T",view=[65,18], color=red,line_width=2,parametric(8/(sqrt(0.5)*sqrt(u)),u,0,u,0.33,20), point_type=7,point_size=1.2,points([[8,2,0]]), color=skyblue,line_width=1,explicit(T(L,K),L,0,20, K,0,20), color=blue,line_width=2,parametric(8/(sqrt(0.5)*sqrt(u)),u,T(8/(sqrt(0.5)*sqrt(u)),u),u,0.33,20), points([[8,2,T(8,2)]]),user_preamble= "set xyplane at 0"),wxplot_size=[700,600]; |