Parcijalne derivacije

primjer 1

(%i1) diff(x^2+y^2,x);
(%o1) 2*x
(%i2) diff(x^2+y^2,y);
(%o2) 2*y

primjer 2

(%i3) diff(3*x^2+x*y+sqrt(y),x);
(%o3) y+6*x
(%i4) diff(3*x^2+x*y+sqrt(y),y);
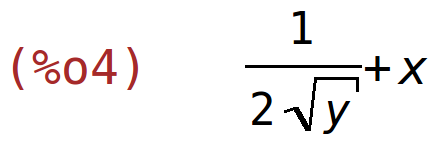
(%o4) 1/(2*sqrt(y))+x

primjer 3

(%i5) diff(y/x,x);
(%o5) -y/x^2
(%i6) diff(y/x,y);
(%o6) 1/x

primjer 4

(%i7) diff((2*x-y)/(x+y),x);
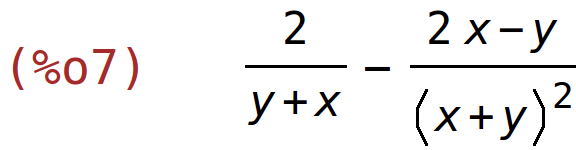
(%o7) 2/(y+x)-(2*x-y)/(x+y)^2
(%i8) factor(%);
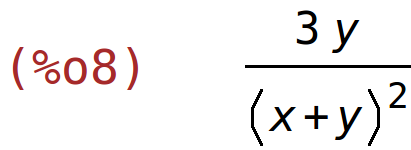
(%o8) (3*y)/(x+y)^2
(%i9) diff((2*x-y)/(x+y),y);
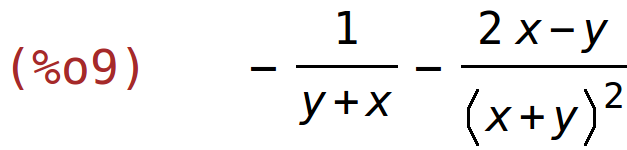
(%o9) -1/(y+x)-(2*x-y)/(x+y)^2
(%i10) factor(%);
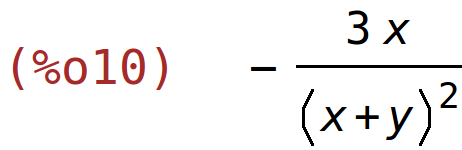
(%o10) -(3*x)/(x+y)^2

primjer 5

(%i11) diff(x*%e^y,x);
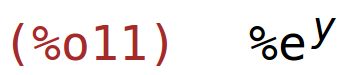
(%o11) %e^y
(%i12) diff(x*%e^y,y);
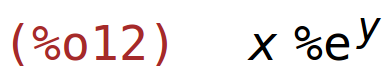
(%o12) x*%e^y

primjer 6

(%i13) diff(y*%e^y+sqrt(x),x);
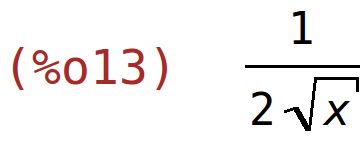
(%o13) 1/(2*sqrt(x))
(%i14) diff(y*%e^y+sqrt(x),y);
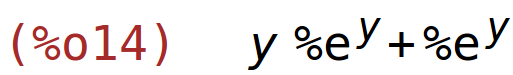
(%o14) y*%e^y+%e^y

primjer 7

(%i15) diff((x+2*y)*%e^(x^2+y^3),x);
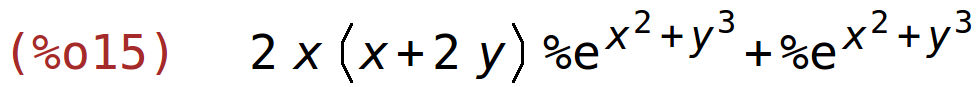
(%o15) 2*x*(x+2*y)*%e^(x^2+y^3)+%e^(x^2+y^3)
(%i16) factor(%);
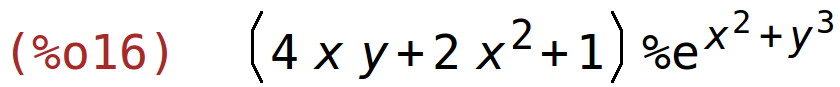
(%o16) (4*x*y+2*x^2+1)*%e^(x^2+y^3)
(%i17) diff((x+2*y)*%e^(x^2+y^3),y);
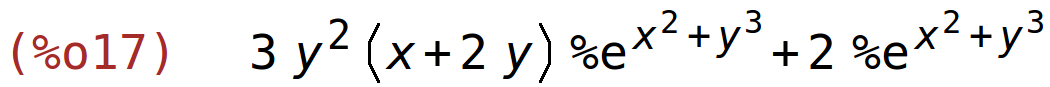
(%o17) 3*y^2*(x+2*y)*%e^(x^2+y^3)+2*%e^(x^2+y^3)
(%i18) factor(%);
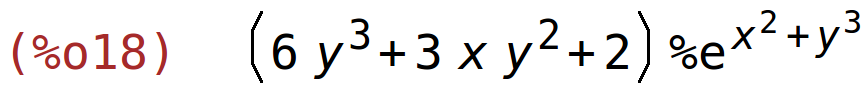
(%o18) (6*y^3+3*x*y^2+2)*%e^(x^2+y^3)

primjer 8

(%i19) diff(x/sqrt(x^2+y^2),x);
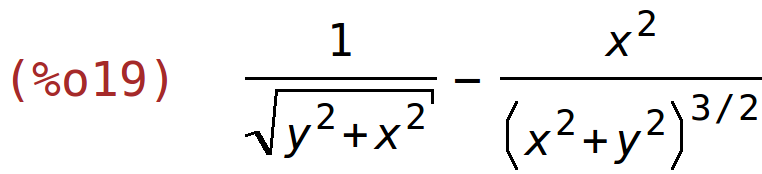
(%o19) 1/sqrt(y^2+x^2)-x^2/(x^2+y^2)^(3/2)
(%i20) factor(%);
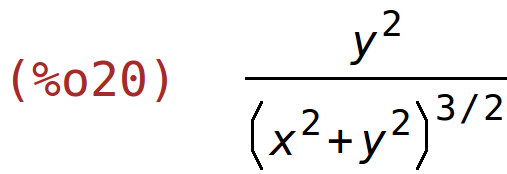
(%o20) y^2/(x^2+y^2)^(3/2)
(%i21) diff(x/sqrt(x^2+y^2),y);
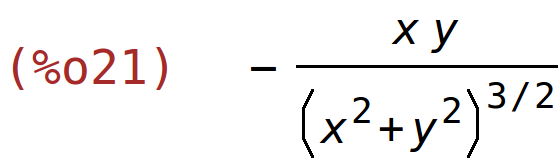
(%o21) -(x*y)/(x^2+y^2)^(3/2)

primjer 9

(%i22) diff(2^sin(y/x),x);
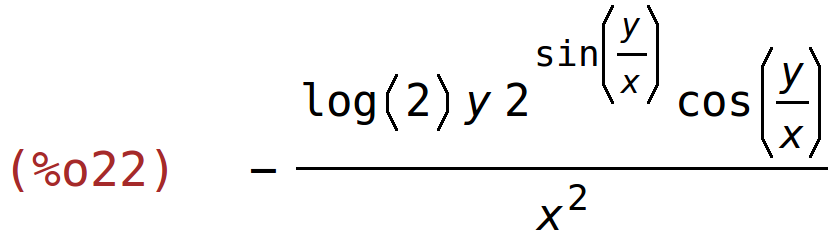
(%o22) -(log(2)*y*2^sin(y/x)*cos(y/x))/x^2
(%i23) diff(2^sin(y/x),y);
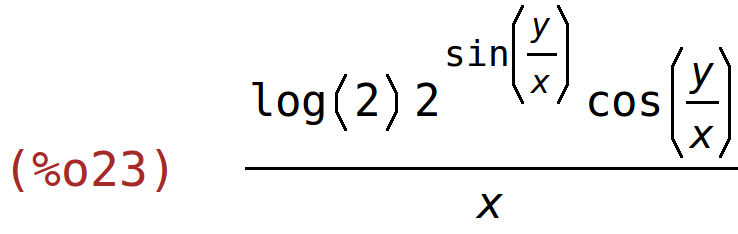
(%o23) (log(2)*2^sin(y/x)*cos(y/x))/x

primjer 10

(%i24) diff(x^y,x);
(%o24) x^(y-1)*y
(%i25) diff(x^y,y);
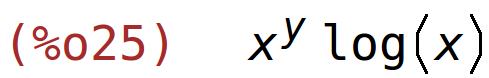
(%o25) x^y*log(x)

primjer 11

(%i26) diff(%e^(2*x*z)-log(y*z)+1,x);
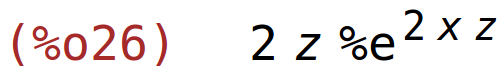
(%o26) 2*z*%e^(2*x*z)
(%i27) diff(%e^(2*x*z)-log(y*z)+1,y);
(%o27) -1/y
(%i28) diff(%e^(2*x*z)-log(y*z)+1,z);
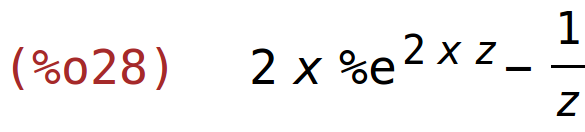
(%o28) 2*x*%e^(2*x*z)-1/z

primjer 12 - računanje vrijednosti parcijalnih derivacija u točki

(%i29) g(x,y,z):=sqrt(x^2-y^2)+sqrt(2*x*z+1)+log(y+%e);
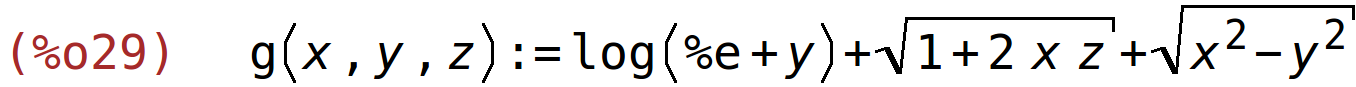
(%o29) g(x,y,z):=log(%e+y)+sqrt(1+2*x*z)+sqrt(x^2-y^2)
(%i30) gx:diff(g(x,y,z),x);
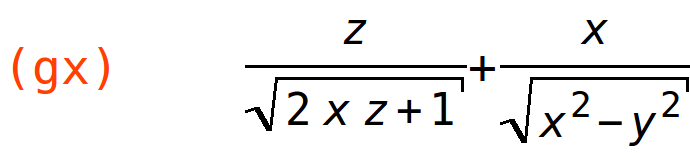
(gx) z/sqrt(2*x*z+1)+x/sqrt(x^2-y^2)
(%i31) subst([x=1,y=0,z=4],gx);
(%o31) 7/3
(%i32) gy:diff(g(x,y,z),y);
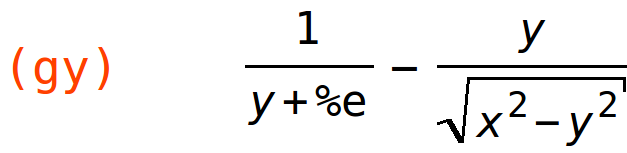
(gy) 1/(y+%e)-y/sqrt(x^2-y^2)
(%i33) subst([x=1,y=0,z=4],gy);
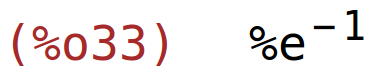
(%o33) %e^(-1)
(%i34) gz:diff(g(x,y,z),z);
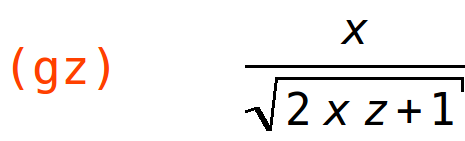
(gz) x/sqrt(2*x*z+1)
(%i35) subst([x=1,y=0,z=4],gz);
(%o35) 1/3

Parcijalne derivacije višeg reda

primjer 1

(%i36) f(x,y):=y^2*2^x;
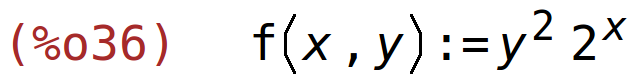
(%o36) f(x,y):=y^2*2^x

parcijalne derivacije prvog reda

(%i37) diff(f(x,y),x);
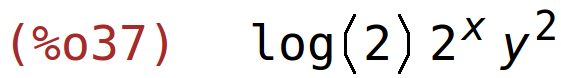
(%o37) log(2)*2^x*y^2
(%i38) diff(f(x,y),y);
(%o38) 2^(1+x)*y

parcijalne derivacije drugog reda

(%i39) diff(f(x,y),x,2);
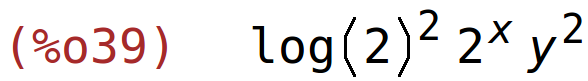
(%o39) log(2)^2*2^x*y^2
(%i40) diff(f(x,y),x,1,y,1);
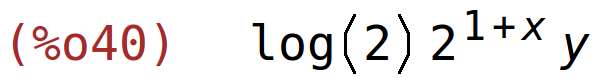
(%o40) log(2)*2^(1+x)*y
(%i41) diff(f(x,y),y,1,x,1);
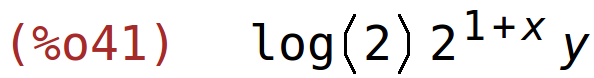
(%o41) log(2)*2^(1+x)*y
(%i42) diff(f(x,y),y,2);
(%o42) 2^(1+x)

primjer 2

(%i43) g(x,y):=log(x^2+y^2);
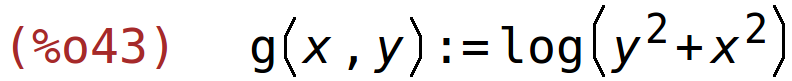
(%o43) g(x,y):=log(y^2+x^2)

parcijalne derivacije prvog reda

(%i44) diff(g(x,y),x);
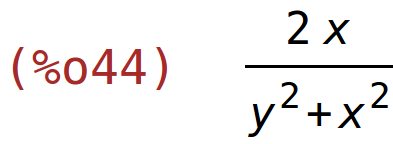
(%o44) (2*x)/(y^2+x^2)
(%i45) diff(g(x,y),y);
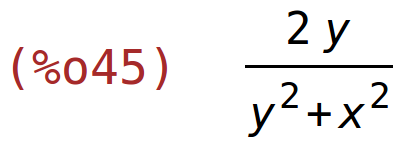
(%o45) (2*y)/(y^2+x^2)

parcijalne derivacije drugog reda

(%i46) diff(g(x,y),x,2);
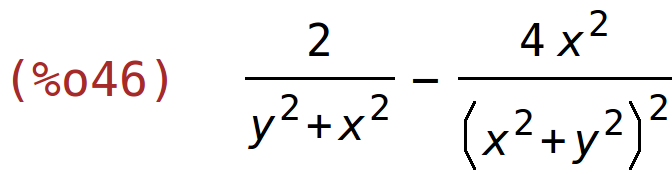
(%o46) 2/(y^2+x^2)-(4*x^2)/(x^2+y^2)^2
(%i47) factor(%);
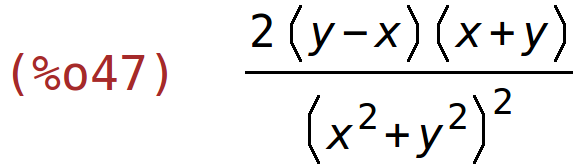
(%o47) (2*(y-x)*(x+y))/(x^2+y^2)^2
(%i48) diff(g(x,y),x,1,y,1);
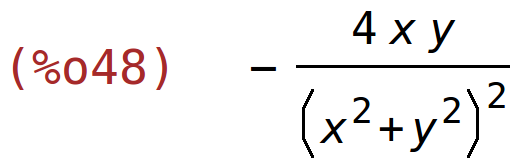
(%o48) -(4*x*y)/(x^2+y^2)^2
(%i49) diff(g(x,y),y,1,x,1);
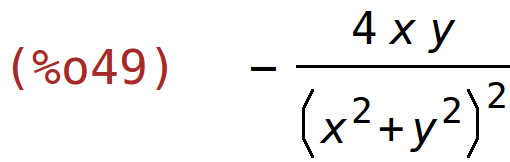
(%o49) -(4*x*y)/(x^2+y^2)^2
(%i50) diff(g(x,y),y,2);
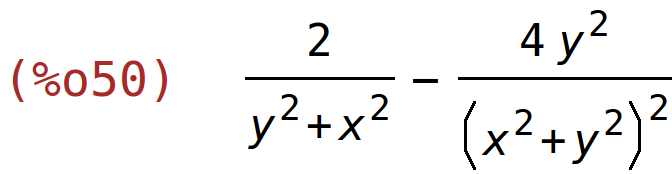
(%o50) 2/(y^2+x^2)-(4*y^2)/(x^2+y^2)^2
(%i51) factor(%);
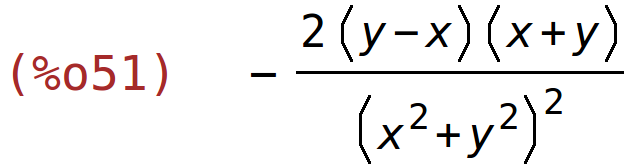
(%o51) -(2*(y-x)*(x+y))/(x^2+y^2)^2

primjer 3 - neke parcijalne derivacije trećeg reda

(%i52) f(x,y,z):=z*y^x;
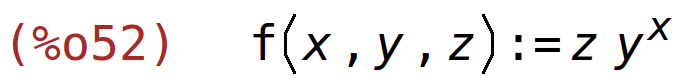
(%o52) f(x,y,z):=z*y^x

jedanput po x, jedanput po y, jedanput po z

(%i53) diff(f(x,y,z),x,1,y,1,z,1);
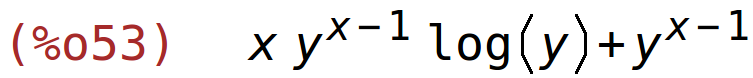
(%o53) x*y^(x-1)*log(y)+y^(x-1)

dvaput po x, jedanput po y

(%i54) diff(f(x,y,z),x,2,y,1);
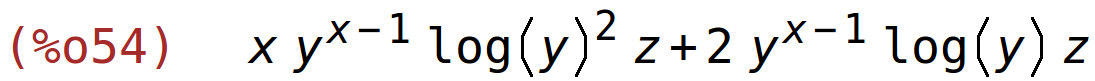
(%o54) x*y^(x-1)*log(y)^2*z+2*y^(x-1)*log(y)*z

dvaput po y, jedanput po z

(%i55) diff(f(x,y,z),y,2,z,1);
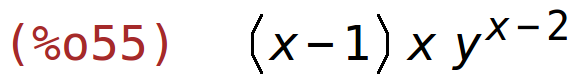
(%o55) (x-1)*x*y^(x-2)

Ekstremi funkcije dvije varijable

primjer 1

(%i56) f(x,y):=80-y^2+x^3+12*y-3*x;
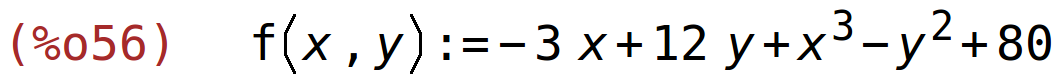
(%o56) f(x,y):=-3*x+12*y+x^3-y^2+80

parcijalne derivacije

(%i57) fx:diff(f(x,y),x);
(fx) 3*x^2-3
(%i58) fy:diff(f(x,y),y);
(fy) 12-2*y

stacionarne točke: (1,6), (-1,6)

(%i59) solve([fx=0,fy=0],[x,y]);
(%o59) [[x=1,y=6],[x=-1,y=6]]

Hesseova matrica funkcije f

(%i60) hesf:hessian(f(x,y),[x,y]);
(hesf) matrix(<BR> [6*x, 0],<BR> [0, -2]<BR> )

Točka (1,6) je sedlasta točka funkcije f.

(%i61) f1:subst([x=1,y=6],hesf);
(f1) matrix(<BR> [6, 0],<BR> [0, -2]<BR> )
(%i62) determinant(f1);
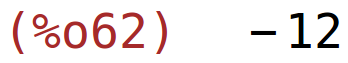
(%o62) -12

U točki (-1,6) funkcija f ima lokalni maksimum koji je jednak 118.

(%i63) f2:subst([x=-1,y=6],hesf);
(f2) matrix(<BR> [-6, 0],<BR> [0, -2]<BR> )
(%i64) determinant(f2);
(%o64) 12
(%i65) f(-1,6);
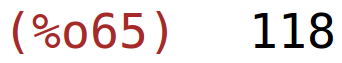
(%o65) 118

3D slika
→ crvena točka je točka lokalnog maksimuma
→ zelena točka je sedlasta točka

(%i66) load(draw)$
(%i67) wxdraw3d(xu_grid=10,yv_grid=10,view=[60,320],zrange=[-600,600],surface_hide=true,
xlabel="x",ylabel="y",zlabel="z",
explicit(80-y^2+x^3+12*y-3*x, x,-7,7, y,-7,25),
color=red,point_type=7,point_size=1.2,points([[-1,6,118]]),
color=sea-green,points([[1,6,114.4]])),wxplot_size=[600,700];
(%t67)
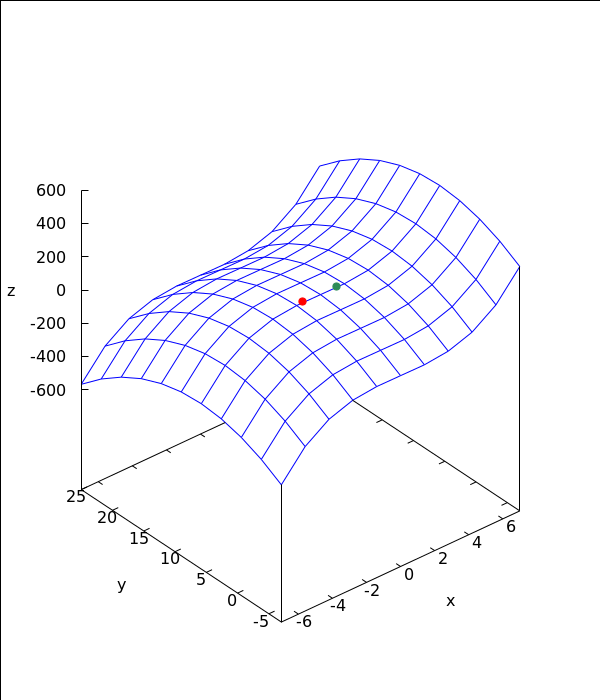
(Graphics)
(%o67)

primjer 2

(%i68) g(x,y):=8/x+x/y+y;
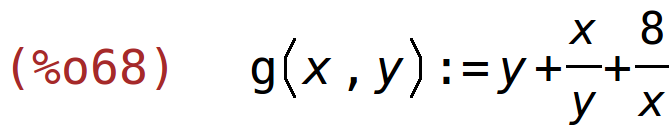
(%o68) g(x,y):=y+x/y+8/x

parcijalne derivacije

(%i69) gx:diff(g(x,y),x);
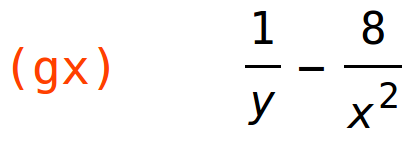
(gx) 1/y-8/x^2
(%i70) gy:diff(g(x,y),y);
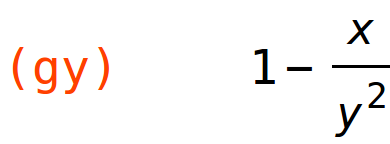
(gy) 1-x/y^2

stacionarne točke: (4,2)
kompleksni brojevi nas ovdje ne zanimaju, a točka (0,0) nije u domeni funkcije g.

(%i71) solve([gx=0,gy=0],[x,y]);
(%o71) [[x=4,y=2],[x=-2*sqrt(3)*%i-2,y=sqrt(3)*%i-1],[x=2*sqrt(3)*%i-2,y=-sqrt(3)*%i-1],[x=0,y=0]]

Hesseova matrica funkcije g

(%i72) hesg:hessian(g(x,y),[x,y]);
(hesg) matrix(<BR> [16/x^3, -1/y^2],<BR> [-1/y^2, (2*x)/y^3]<BR> )

U točki (4,2) funkcija g ima lokalni minimum koji je jednak 6.

(%i73) g1:subst([x=4,y=2],hesg);
(g1) matrix(<BR> [1/4, -1/4],<BR> [-1/4, 1]<BR> )
(%i74) determinant(g1);
(%o74) 3/16
(%i75) g(4,2);
(%o75) 6

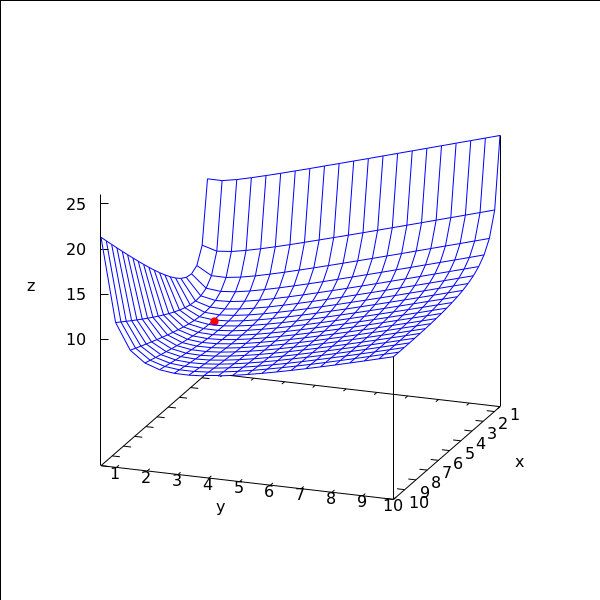
3D slika
→ crvena točka je točka lokalnog minimuma

(%i76) wxdraw3d(xu_grid=20,yv_grid=20,view=[70,110],surface_hide=true,
xlabel="x",ylabel="y",zlabel="z",
explicit(8/x+x/y+y, x,0.5,10, y,0.5,10),
color=red,point_type=7,point_size=1.2,points([[4,2,6.1]])),wxplot_size=[600,600];
(%t76)
(Graphics)
(%o76)

Uvjetni ekstremi funkcije dvije varijable

primjer 1
Odredite ekstreme funkcije f(x,y)=e^(xy) uz uvjet x+y=4.

(%i77) f(x,y):=%e^(x*y);
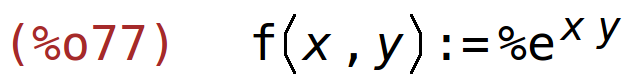
(%o77) f(x,y):=%e^(x*y)

iz uvjeta izrazimo varijablu y pomoću varijable x i uvrstimo u funkciju f

(%i78) solve(x+y=4,y);
(%o78) [y=4-x]
(%i79) f(x,4-x);
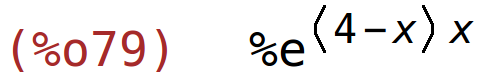
(%o79) %e^((4-x)*x)

dobivamo funkciju jedne varijable čije ekstreme tražimo na standardni način

(%i80) der:diff(f(x,4-x),x);
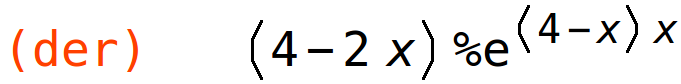
(der) (4-2*x)*%e^((4-x)*x)

stacionarna točka: 2

(%i81) solve(der=0,x);
(%o81) [x=2]

U točki 2 imamo lokalni maksimum

(%i82) der2:diff(f(x,4-x),x,2);
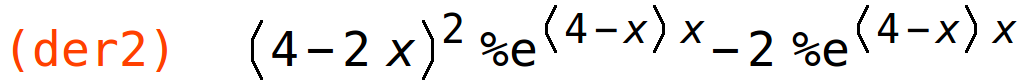
(der2) (4-2*x)^2*%e^((4-x)*x)-2*%e^((4-x)*x)
(%i83) subst(x=2,der2);
(%o83) -2*%e^4

Uvrstimo x=2 u y=4-x pa dobivamo da je y=2
Dakle, funkcija f postiže lokalnu uvjetni maksimum u točki (2,2) i on iznosi e^4.

(%i84) f(2,2);
(%o84) %e^4

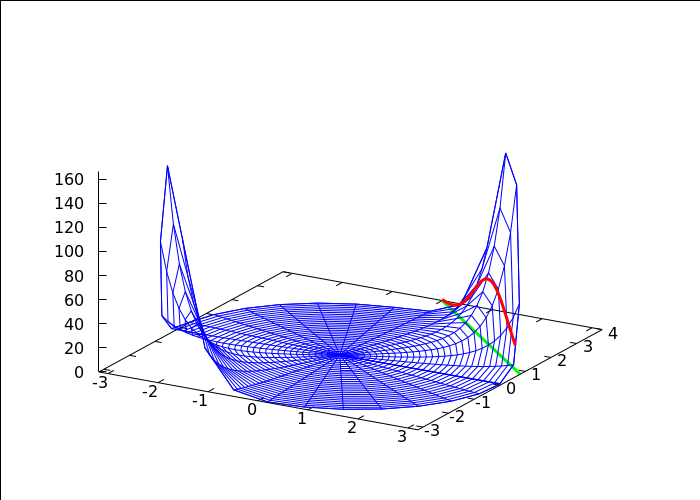
3D slika
→ graf funkcije f je plava ploha
→ tražimo ekstreme funkcije f samo na zelenom pravcu u domeni
→ u tom slučaju gledamo samo crvenu krivulju na zadanoj plohi
→ vidimo na slici da postoji najviša točka na toj crvenoj krivulji

(%i85) wxdraw3d(
color=green,line_width=3,
parametric(u,4-u,0,u,0,3.2),
surface_hide = false, color=blue,line_width=1,
parametric_surface(u*cos(v),u*sin(v),%e^(u^2*cos(v)*sin(v)),u,0,3.2,v,0,6.29),color=red,line_width=3,
parametric(u,4-u,%e^(u*(4-u)),u,0,3),
user_preamble= "set xyplane at 0"),wxplot_size=[700,500];
(%t85)
(Graphics)
(%o85)

primjer 2
Odredite ekstreme funkcije f(x,y)=-x-y uz uvjet x^2+y^2=2.

(%i86) f(x,y):=-x-y;
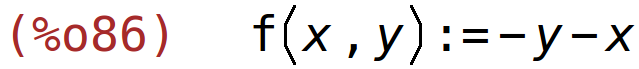
(%o86) f(x,y):=-y-x

definiramo Lagrangeovu funkciju

(%i87) L(x,y,l):=-x-y+l*(x^2+y^2-2);
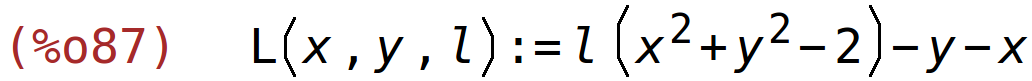
(%o87) L(x,y,l):=l*(x^2+y^2-2)-y-x

parcijalne derivacije Lagrangeove funkcije

(%i88) Lx:diff(L(x,y,l),x);
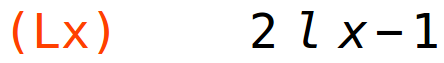
(Lx) 2*l*x-1
(%i89) Ly:diff(L(x,y,l),y);
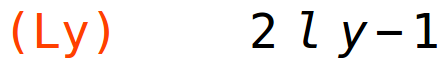
(Ly) 2*l*y-1
(%i90) Ll:diff(L(x,y,l),l);
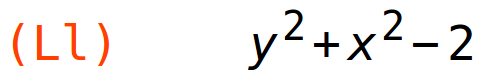
(Ll) y^2+x^2-2

Stacionarne točke: (-1,-1), (1,1)

(%i91) solve([Lx=0,Ly=0,Ll=0],[x,y,l]);
(%o91) [[x=-1,y=-1,l=-1/2],[x=1,y=1,l=1/2]]

U točki (-1,-1) funkcija f postiže uvjetni maksimum koji je jednak 2.
U točki (1,1) funkcija f postiže uvjetni minimum koji je jednak -2.

(%i92) f(1,1);
(%o92) -2
(%i93) f(-1,-1);
(%o93) 2

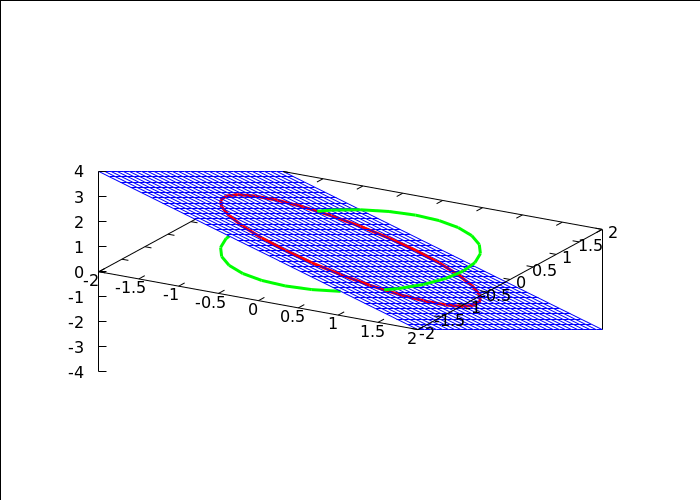
3D slika
→ graf funkcije f je plava ravnina
→ tražimo ekstreme funkcije f samo na zelenoj kružnici u domeni
→ ako gledamo samo zelenu kružnicu u domeni, to je isto kao da na plavoj ravnini gledamo samo crvenu krivulju
→ sa slike je vidljivo da na crvenoj krivulji postoji najviša i najniža točka

(%i94) wxdraw3d(surface_hide = true,
explicit(-x-y,x,-2,2,y,-2,2),color=red,line_width=3,
parametric(sqrt(2)*cos(u),sqrt(2)*sin(u),-sqrt(2)*cos(u)-sqrt(2)*sin(u),u,0,6.28),
color=green,
parametric(sqrt(2)*cos(u),sqrt(2)*sin(u),0,u,0,6.28),
user_preamble= "set xyplane at 0"),wxplot_size=[700,500];
(%t94)
(Graphics)
(%o94)
Created with wxMaxima.