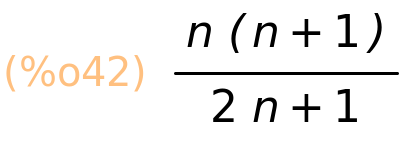1 Računanje faktorijela

(%i1) 5!;
(%o1) 120
(%i2) 10!;
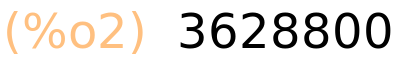
(%o2) 3628800
(%i3) 100!;
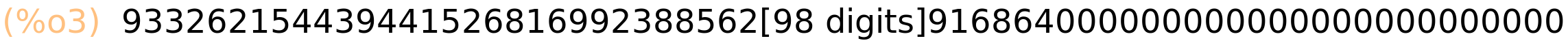
(%o3) 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
(%i4) set_display('ascii)$
(%i5) 100!;
(%o5) 933262154439441526816992388562667004907159682643816214685929638952175999\<BR> 932299156089414639761565182862536979208272237582511852109168640000000000000000\<BR> 00000000
(%i6) set_display('xml)$

 2 Binomni koeficijenti

(%i7) binomial(6,4);
(%o7) 15
(%i8) binomial(n,0);
(%o8) 1
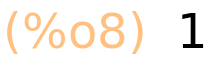
(%i9) binomial(n,1);
(%o9) n
(%i10) binomial(n,n);
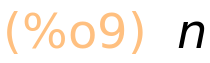
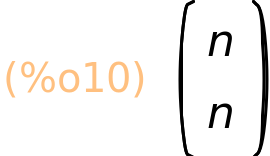
(%o10) (binomial(n,n))
(%i11) binomial(100,98);
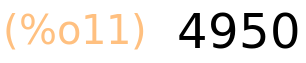
(%o11) 4950
(%i12) binomial(234,126);
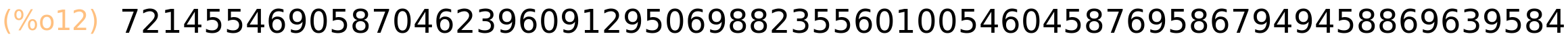
(%o12) 721455469058704623960912950698823556010054604587695867949458869639584

 3 Binomni poučak

(%i13) expand((a+b)^11);
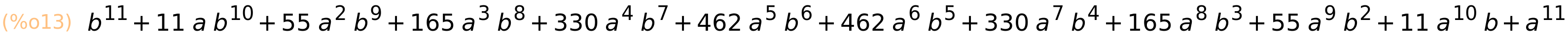
(%o13) b^11+11*a*b^10+55*a^2*b^9+165*a^3*b^8+330*a^4*b^7+462*a^5*b^6+462*a^6*b^5+330*a^7*b^4+165*a^8*b^3+55*a^9*b^2+11*a^10*b+a^11
(%i14) expand((a+b)^100);
(%o14) b^100+100*a*b^99+4950*a^2*b^98+161700*a^3*b^97+3921225*a^4*b^96+75287520*a^5*b^95+1192052400*a^6*b^94+16007560800*a^7*b^93+186087894300*a^8*b^92+1902231808400*a^9*b^91+17310309456440*a^10*b^90+141629804643600*a^11*b^89+1050421051106700*a^12*b^88+7110542499799200*a^13*b^87+44186942677323600*a^14*b^86+253338471349988640*a^15*b^85+1345860629046814650*a^16*b^84+6650134872937201800*a^17*b^83+30664510802988208300*a^18*b^82+132341572939212267400*a^19*b^81+535983370403809682970*a^20*b^80+2041841411062132125600*a^21*b^79+7332066885177656269200*a^22*b^78+24865270306254660391200*a^23*b^77+79776075565900368755100*a^24*b^76+242519269720337121015504*a^25*b^75+699574816500972464467800*a^26*b^74+1917353200780443050763600*a^27*b^73+4998813702034726525205100*a^28*b^72+12410847811948286545336800*a^29*b^71+29372339821610944823963760*a^30*b^70+66324638306863423796047200*a^31*b^69+143012501349174257560226775*a^32*b^68+294692427022540894366527900*a^33*b^67+580717429720889409486981450*a^34*b^66+1095067153187962886461165020*a^35*b^65+1977204582144932989443770175*a^36*b^64+3420029547493938143902737600*a^37*b^63+5670048986634686922786117600*a^38*b^62+9013924030034630492634340800*a^39*b^61+13746234145802811501267369720*a^40*b^60+20116440213369968050635175200*a^41*b^59+28258808871162574166368460400*a^42*b^58+38116532895986727945334202400*a^43*b^57+49378235797073715747364762200*a^44*b^56+61448471214136179596720592960*a^45*b^55+73470998190814997343905056800*a^46*b^54+84413487283064039501507937600*a^47*b^53+93206558875049876949581681100*a^48*b^52+98913082887808032681188722800*a^49*b^51+100891344545564193334812497256*a^50*b^50+98913082887808032681188722800*a^51*b^49+93206558875049876949581681100*a^52*b^48+84413487283064039501507937600*a^53*b^47+73470998190814997343905056800*a^54*b^46+61448471214136179596720592960*a^55*b^45+49378235797073715747364762200*a^56*b^44+38116532895986727945334202400*a^57*b^43+28258808871162574166368460400*a^58*b^42+20116440213369968050635175200*a^59*b^41+13746234145802811501267369720*a^60*b^40+9013924030034630492634340800*a^61*b^39+5670048986634686922786117600*a^62*b^38+3420029547493938143902737600*a^63*b^37+1977204582144932989443770175*a^64*b^36+1095067153187962886461165020*a^65*b^35+580717429720889409486981450*a^66*b^34+294692427022540894366527900*a^67*b^33+143012501349174257560226775*a^68*b^32+66324638306863423796047200*a^69*b^31+29372339821610944823963760*a^70*b^30+12410847811948286545336800*a^71*b^29+4998813702034726525205100*a^72*b^28+1917353200780443050763600*a^73*b^27+699574816500972464467800*a^74*b^26+242519269720337121015504*a^75*b^25+79776075565900368755100*a^76*b^24+24865270306254660391200*a^77*b^23+7332066885177656269200*a^78*b^22+2041841411062132125600*a^79*b^21+535983370403809682970*a^80*b^20+132341572939212267400*a^81*b^19+30664510802988208300*a^82*b^18+6650134872937201800*a^83*b^17+1345860629046814650*a^84*b^16+253338471349988640*a^85*b^15+44186942677323600*a^86*b^14+7110542499799200*a^87*b^13+1050421051106700*a^88*b^12+141629804643600*a^89*b^11+17310309456440*a^90*b^10+1902231808400*a^91*b^9+186087894300*a^92*b^8+16007560800*a^93*b^7+1192052400*a^94*b^6+75287520*a^95*b^5+3921225*a^96*b^4+161700*a^97*b^3+4950*a^98*b^2+100*a^99*b+a^100

  1. primjer

(%i15) expand((x^(1/3)+x^2)^4);
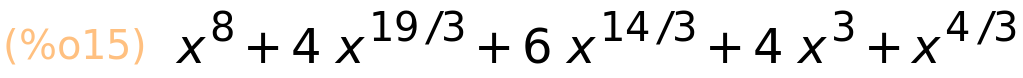
(%o15) x^8+4*x^(19/3)+6*x^(14/3)+4*x^3+x^(4/3)

  2. primjer

(%i16) expand((x^(1/3)−x^2)^4);
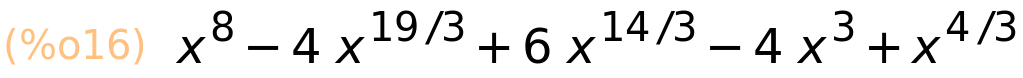
(%o16) x^8-4*x^(19/3)+6*x^(14/3)-4*x^3+x^(4/3)

  3. primjer

(%i17) expand((x^(3/2)·y+y^(−1))^5);
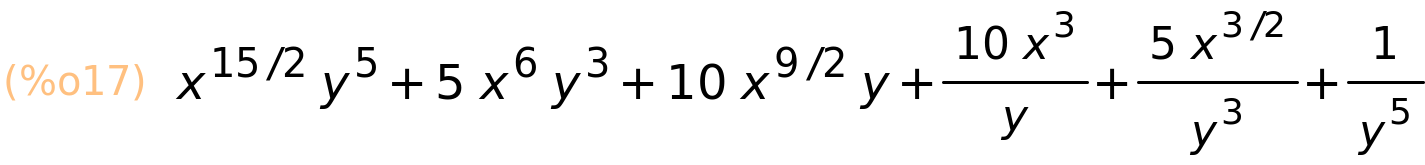
(%o17) x^(15/2)*y^5+5*x^6*y^3+10*x^(9/2)*y+(10*x^3)/y+(5*x^(3/2))/y^3+1/y^5

 4 Matematička indukcija (računanje suma)

 4.1 prva suma

  Maxima bez problema računa sume s konkretnom donjom i gornjom granicom brojača

(%i18) sum(2·i·(3·i−1),i,1,23);
(%o18) 25392
(%i19) sum(2·i·(3·i−1),i,1,321);
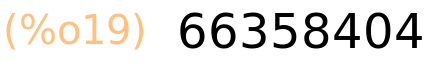
(%o19) 66358404
(%i20) sum(2·i·(3·i−1),i,150,321);
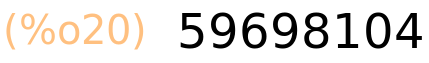
(%o20) 59698104

  Maxima ne izračuna automatski simboličke sume

(%i21) sum(2·i·(3·i−1),i,1,n);
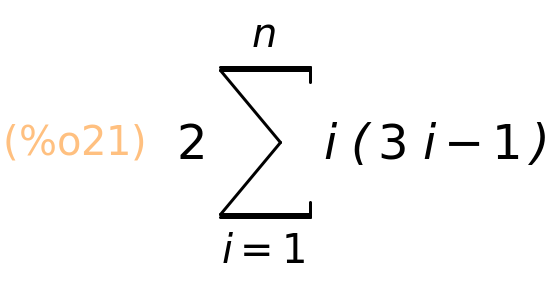
(%o21) 2*sum(i*(3*i-1),i,1,n)

  Uz dodatne naredbe ju možemo natjerati da izračuna neke simboličke sume

(%i22) sum(2·i·(3·i−1),i,1,n),simpsum;
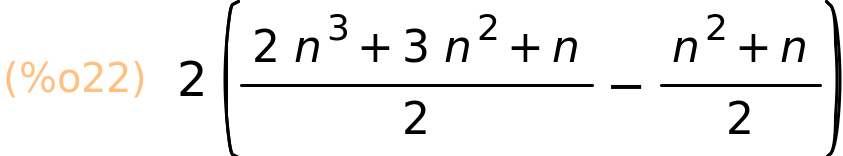
(%o22) 2*((2*n^3+3*n^2+n)/2-(n^2+n)/2)
(%i23) factor(%);
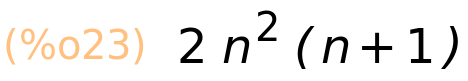
(%o23) 2*n^2*(n+1)

 4.2 Numeričko računanje sume

(%i24) sum(sin(i),i,1,20);
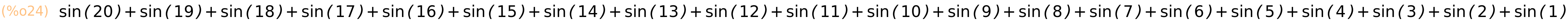
(%o24) sin(20)+sin(19)+sin(18)+sin(17)+sin(16)+sin(15)+sin(14)+sin(13)+sin(12)+sin(11)+sin(10)+sin(9)+sin(8)+sin(7)+sin(6)+sin(5)+sin(4)+sin(3)+sin(2)+sin(1)

U ovakvim situacijama uvijek je pametnije numerički odrediti sumu kako bismo spriječili eventualno rušenje grafičkog sučelja zbog prevelikog broja simboličkih članova u sumi. Na primjer, da je suma išla od i=1 do i=10000, maxima ne bi ništa napravila osim ispisala ogromni izraz koji bi mogao srušiti grafičko sučelje. Kod numeričkog računa to se neće dogoditi.

(%i25) sum(sin(i),i,1,20),numer;
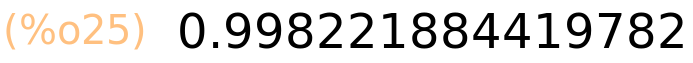
(%o25) 0.998221884419782
(%i26) sum(sin(i),i,1,10000),numer;
(%o26) 1.633891021792447

 4.3 druga suma

(%i27) suma2:sum((−1)^i·(2·i−1),i,1,n);
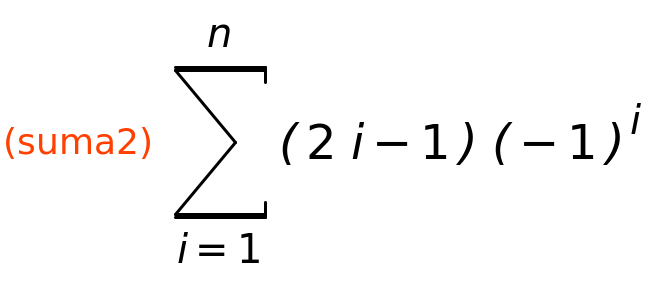
(suma2) sum((2*i-1)*(-1)^i,i,1,n)
(%i28) sum((−1)^i·(2·i−1),i,1,37);
(%o28) -37
(%i29) sum((−1)^i·(2·i−1),i,1,120);
(%o29) 120

  Ovaj put Maxima ne može izračunati simboličku sumu

(%i30) suma2,simpsum;
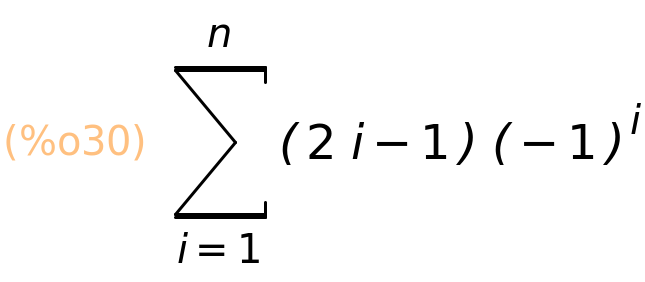
(%o30) sum((2*i-1)*(-1)^i,i,1,n)

  Međutim, možemo nepotpunom indukcijom zaključiti da je ta suma jednaka

(%i31) (−1)^n·n;
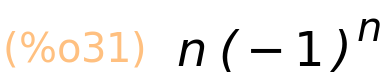
(%o31) n*(-1)^n
(%i32) makelist(sum((−1)^i·(2·i−1),i,1,n),n,1,200);
(%o32) [-1,2,-3,4,-5,6,-7,8,-9,10,-11,12,-13,14,-15,16,-17,18,-19,20,-21,22,-23,24,-25,26,-27,28,-29,30,-31,32,-33,34,-35,36,-37,38,-39,40,-41,42,-43,44,-45,46,-47,48,-49,50,-51,52,-53,54,-55,56,-57,58,-59,60,-61,62,-63,64,-65,66,-67,68,-69,70,-71,72,-73,74,-75,76,-77,78,-79,80,-81,82,-83,84,-85,86,-87,88,-89,90,-91,92,-93,94,-95,96,-97,98,-99,100,-101,102,-103,104,-105,106,-107,108,-109,110,-111,112,-113,114,-115,116,-117,118,-119,120,-121,122,-123,124,-125,126,-127,128,-129,130,-131,132,-133,134,-135,136,-137,138,-139,140,-141,142,-143,144,-145,146,-147,148,-149,150,-151,152,-153,154,-155,156,-157,158,-159,160,-161,162,-163,164,-165,166,-167,168,-169,170,-171,172,-173,174,-175,176,-177,178,-179,180,-181,182,-183,184,-185,186,-187,188,-189,190,-191,192,-193,194,-195,196,-197,198,-199,200]

  Ili pak možemo učitati dodatni paket koji omogućuje računanje kompliciranijih suma

(%i33) load (zeilberger)$
(%i34) GosperSum((−1)^i·(2·i−1),i,1,n);
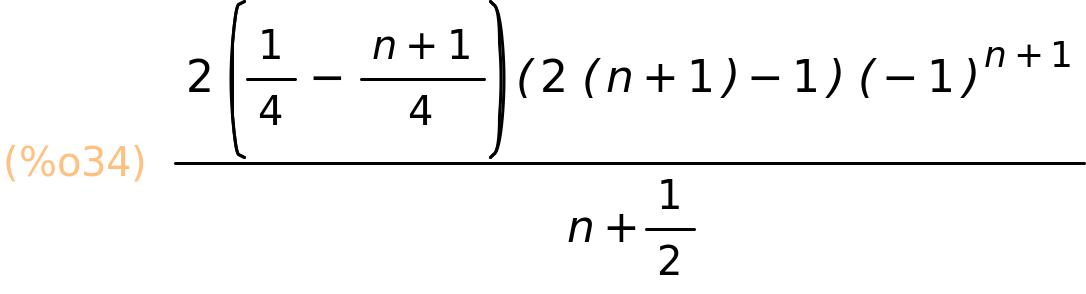
(%o34) (2*(1/4-(n+1)/4)*(2*(n+1)-1)*(-1)^(n+1))/(n+1/2)
(%i35) ratsimp(%);
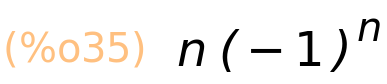
(%o35) n*(-1)^n

 4.4 treća suma

(%i36) suma3:sum(2·i^2/((2·i−1)·(2·i+1)),i,1,n);
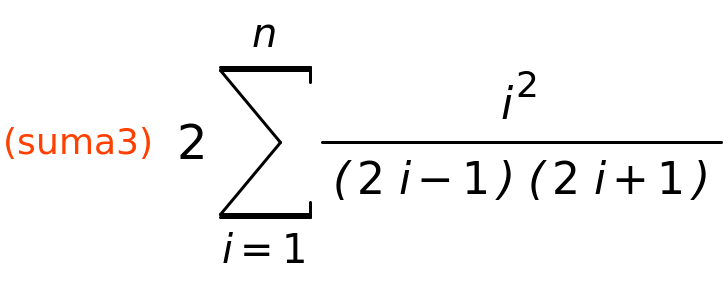
(suma3) 2*sum(i^2/((2*i-1)*(2*i+1)),i,1,n)
(%i37) sum(2·i^2/((2·i−1)·(2·i+1)),i,1,98);
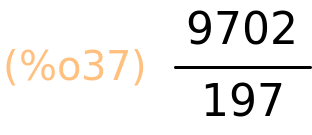
(%o37) 9702/197
(%i38) sum(2·i^2/((2·i−1)·(2·i+1)),i,5,98);
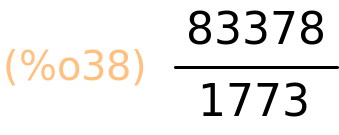
(%o38) 83378/1773
(%i39) sum(2·i^2/((2·i−1)·(2·i+1)),i,1,n),simpsum;
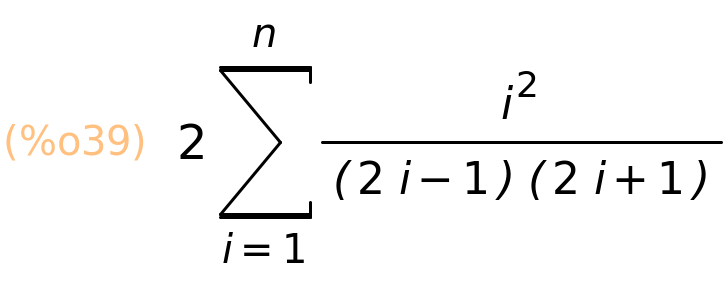
(%o39) 2*sum(i^2/((2*i-1)*(2*i+1)),i,1,n)

  GosperSum će ponovo uspjeti izračunati ovu sumu

(%i40) GosperSum(2·i^2/((2·i−1)·(2·i+1)),i,1,n);
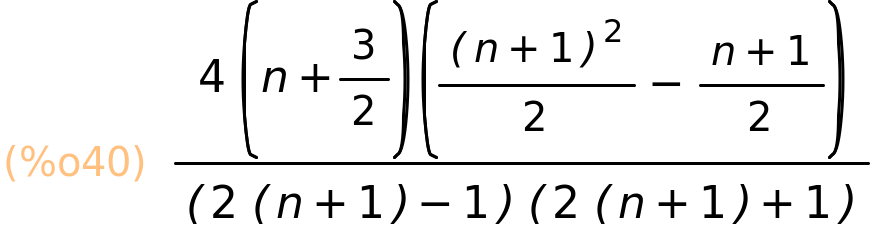
(%o40) (4*(n+3/2)*((n+1)^2/2-(n+1)/2))/((2*(n+1)-1)*(2*(n+1)+1))
(%i41) ratsimp(%);
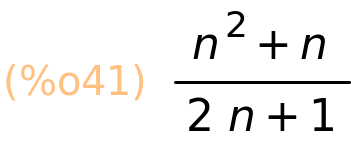
(%o41) (n^2+n)/(2*n+1)
(%i42) factor(%);
(%o42) (n*(n+1))/(2*n+1)
Created with wxMaxima.