(%i1) load(draw)$

1 Tangenta i normala na graf funkcije

Definiramo dvije funkcije koje će nam u zadanoj točki na grafu funkcije pronaći tangentu i normalu.
Degenerirani slučajevi (tangenta i normala su paralelne s koordinatnim osima) nisu posebno razmatrani
kako ne bismo previše komplicirali kod.

(%i2) tangenta(fun,x,x0):=block([der: subst(x0,x,diff(fun,x)),y0:subst(x0,x,fun)], y=der*x+y0-x0*der)$
(%i3) normala(fun,x,x0):=block([der: subst(x0,x,-1/diff(fun,x)),y0:subst(x0,x,fun)], y=der*x+y0-x0*der)$

1. zadatak

(%i4) f(x):=%e^(sin(x)^2);
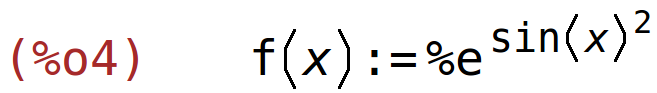
(%o4) f(x):=%e^sin(x)^2

vrijednost funkcije u pi/6

(%i5) f(%pi/6);
(%o5) %e^(1/4)

tangenta

(%i6) tangenta(f(x),x,%pi/6);
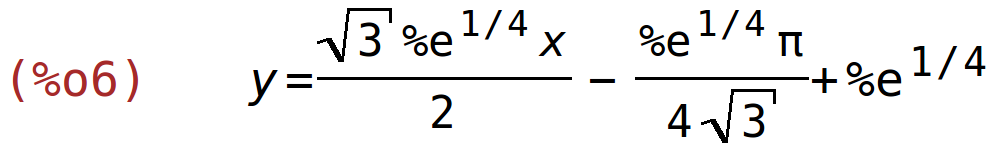
(%o6) y=(sqrt(3)*%e^(1/4)*x)/2-(%e^(1/4)*%pi)/(4*sqrt(3))+%e^(1/4)

normala

(%i7) normala(f(x),x,%pi/6);
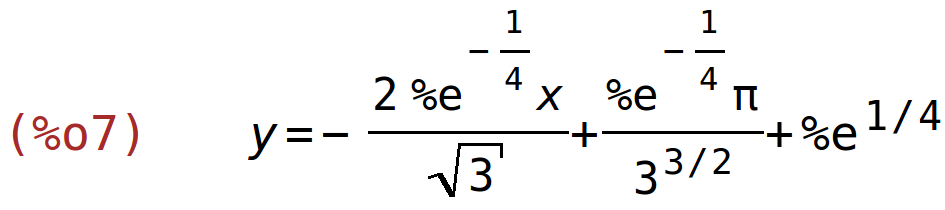
(%o7) y=-(2*%e^(-1/4)*x)/sqrt(3)+(%e^(-1/4)*%pi)/3^(3/2)+%e^(1/4)
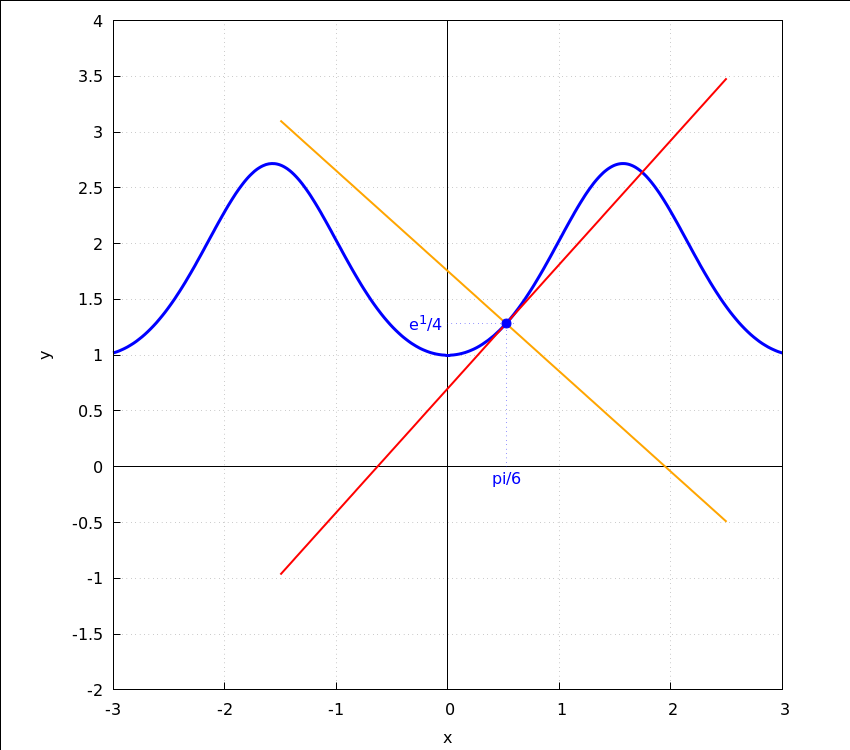
(%i8) wxdraw2d(user_preamble="set size ratio 1",
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-3,1,3],ytics=[-2,0.5,20],explicit(f(x),x,-3,3),line_width=2,color=red,
explicit(rhs(tangenta(f(x),x,%pi/6)),x,-1.5,2.5),color="orange",
explicit(rhs(normala(f(x),x,%pi/6)),x,-1.5,2.5),
color="blue",
point_type=filled_circle,point_size=1.5,
points([[%pi/6,f(%pi/6)]]),
line_type=dots,line_width=1,
parametric(%pi/6,t,t,0,%e^(1/4)),
parametric(t,%e^(1/4),t,0,0.6),
yrange=[-2,4],
label(["pi/6",%pi/6,-0.1]),label(["e^1/4",-0.2,%e^(1/4)])),wxplot_size=[850,750];
(%t8)
(Graphics)
(%o8)
(%i9) draw2d(terminal=wxt,user_preamble="set size ratio 1",
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-3,1,3],ytics=[-2,0.5,20],explicit(f(x),x,-3,3),line_width=2,color=red,
explicit(rhs(tangenta(f(x),x,%pi/6)),x,-1.5,2.5),color="orange",
explicit(rhs(normala(f(x),x,%pi/6)),x,-1.5,2.5),
color="blue",
point_type=filled_circle,point_size=1.5,
points([[%pi/6,f(%pi/6)]]),
line_type=dots,
parametric(%pi/6,t,t,0,%e^(1/4)),
parametric(t,%e^(1/4),t,0,%pi/6),
yrange=[-2,4],
label(["pi/6",%pi/6,-0.1]),label(["e^(1/4)",-0.2,%e^(1/4)]));
(%o9) [gr2d(explicit,explicit,explicit,points,parametric,parametric,label,label)]

duljina odsječka tangente između koordinatnih osi

(%i10) yos:subst(0,x,rhs(tangenta(f(x),x,%pi/6)));
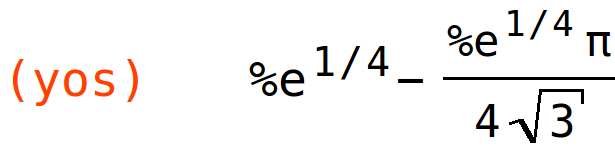
(yos) %e^(1/4)-(%e^(1/4)*%pi)/(4*sqrt(3))
(%i11) xos:rhs(solve(rhs(tangenta(f(x),x,%pi/6))=0,x)[1]);
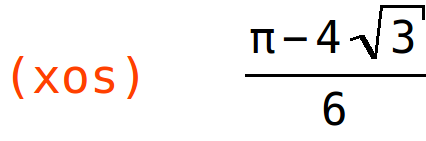
(xos) (%pi-4*sqrt(3))/6
(%i12) float(sqrt(xos^2+yos^2));
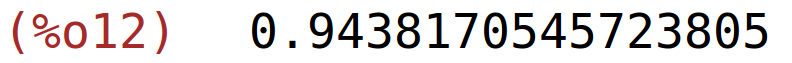
(%o12) 0.9438170545723805

2. zadatak - tangenta na graf funkcije paralelna sa zadanim pravcem

(%i13) f(x):=(x-1)/(x+1);
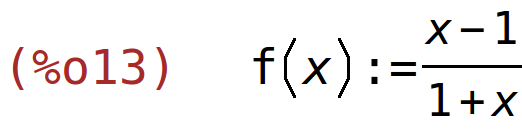
(%o13) f(x):=(x-1)/(1+x)
(%i14) diff(f(x),x);
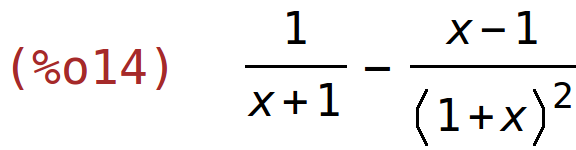
(%o14) 1/(x+1)-(x-1)/(1+x)^2
(%i15) izraz:ratsimp(diff(f(x),x));
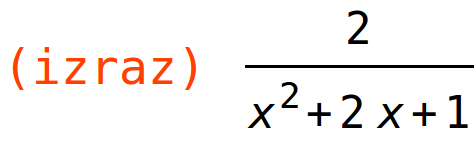
(izraz) 2/(x^2+2*x+1)
(%i16) solve(izraz=2,x);
(%o16) [x=-2,x=0]

točke na grafu

(%i17) [[-2,f(-2)],[0,f(0)]];
(%o17) [[-2,3],[0,-1]]

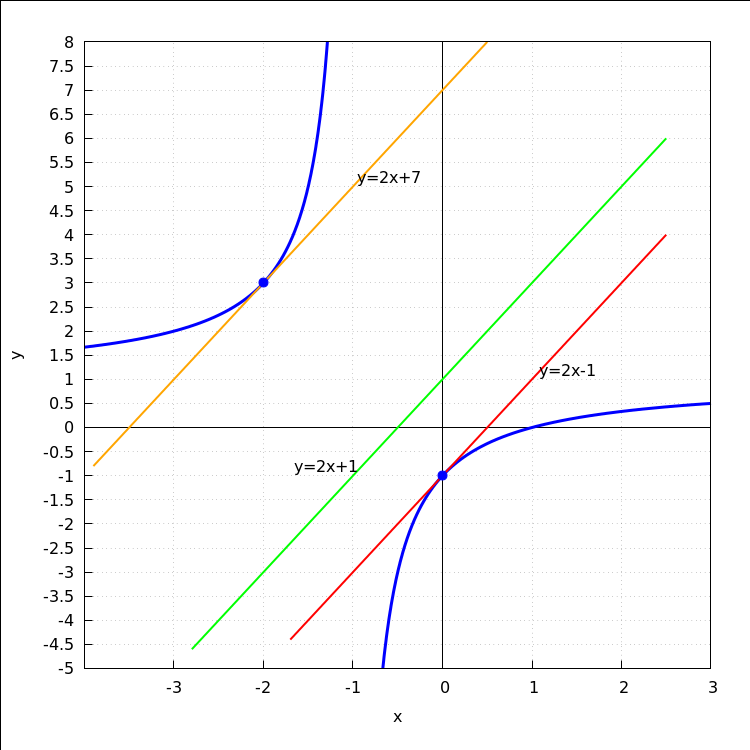
tražene tangente su

(%i18) tangenta(f(x),x,0);
(%o18) y=2*x-1
(%i19) tangenta(f(x),x,-2);
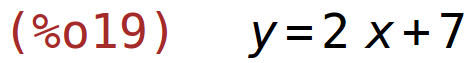
(%o19) y=2*x+7

slika

(%i20) wxdraw2d(user_preamble="set size ratio 1",nticks=100,
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-3,1,3],ytics=[-5,0.5,8],explicit(f(x),x,-4,3),line_width=2,color=red,
explicit(rhs(tangenta(f(x),x,0)),x,-1.7,2.5),color="orange",
explicit(rhs(tangenta(f(x),x,-2)),x,-3.9,0.5),
color="green",
explicit(2*x+1,x,-2.8,2.5),
color="blue",
point_type=filled_circle,point_size=1.5,
points([[-2,f(-2)],[0,f(0)]]),
color="black",
yrange=[-5,8],label(["y=2x+1",-1.3,-0.8]),
label(["y=2x+7",-0.6,5.2]),label(["y=2x-1",1.4,1.2])),wxplot_size=[750,750];
(%t20)
(Graphics)
(%o20)
(%i21) draw2d(terminal=wxt,user_preamble="set size ratio 1",
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-3,1,3],ytics=[-5,0.5,8],explicit(f(x),x,-4,3),line_width=2,color=red,
explicit(rhs(tangenta(f(x),x,0)),x,-1.7,2.5),color="orange",
explicit(rhs(tangenta(f(x),x,-2)),x,-3.9,0.5),
color="green",
explicit(2*x+1,x,-2.8,2.5),
color="blue",
point_type=filled_circle,point_size=1.5,
points([[-2,f(-2)],[0,f(0)]]),
color="black",
yrange=[-5,8],label(["y=2x+1",-1.3,-0.8]),
label(["y=2x+7",-0.6,5.2]),label(["y=2x-1",1.4,1.2]));
(%o21) [gr2d(explicit,explicit,explicit,explicit,points,label,label,label)]

3. zadatak - tangenta i normala paralelne s koordinatnim osima

(%i22) f(x):=2*(x^2-1)^(1/3);
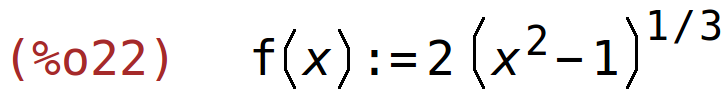
(%o22) f(x):=2*(x^2-1)^(1/3)
(%i23) f(0);
(%o23) -2
(%i24) diff(f(x),x);
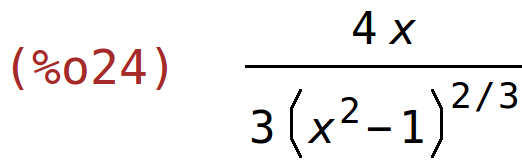
(%o24) (4*x)/(3*(x^2-1)^(2/3))

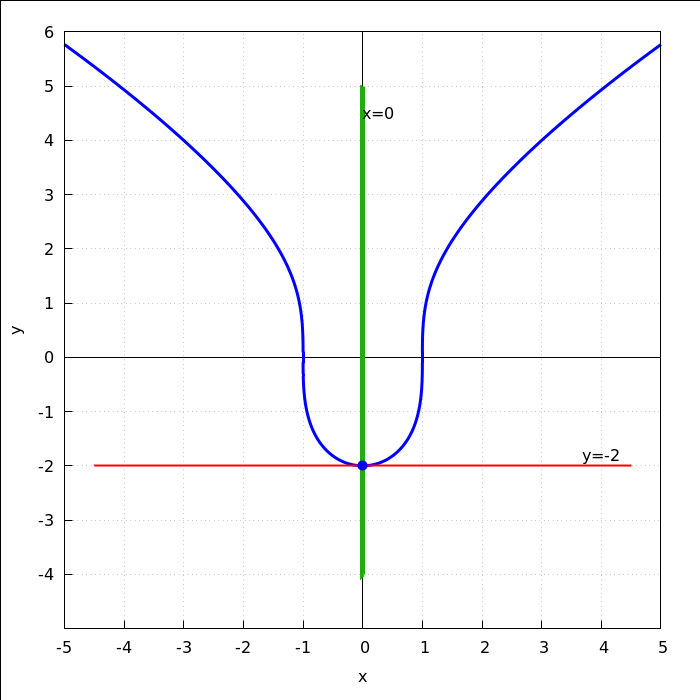
kod normale dobivamo error jer se dijeli s nulom zbog f'(0)=0, a taj slučaj u definiciji funkcije
"normala" nismo posebno razmatrali. No, mi znamo da je u tom slučaju normala okomita na x-os pa je
njezina jednadžba jednaka x=x0, tj. u našem slučaju x=0.

(%i25) tangenta(f(x),x,0);
(%o25) y=-2
(%i26) normala(f(x),x,0);
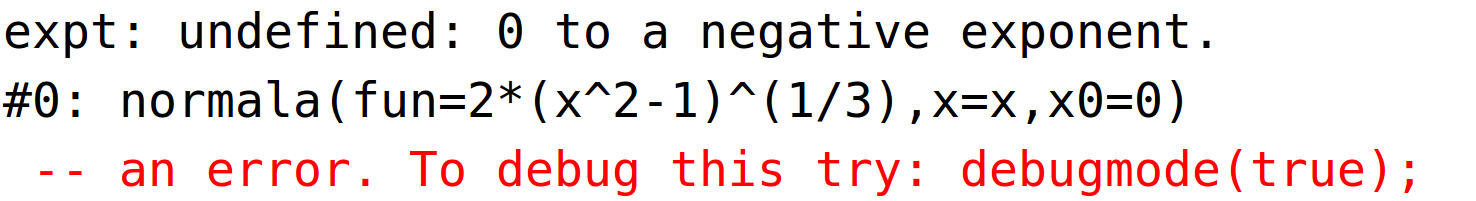
expt: undefined: 0 to a negative exponent.#0: normala(fun=2*(x^2-1)^(1/3),x=x,x0=0)<BR> -- an error. To debug this try: debugmode(true);<BR>
(%i27) wxdraw2d(user_preamble="set size ratio 1",nticks=100,
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-5,1,5],ytics=[-4,1,6],explicit(f(x),x,-5,5),line_width=2,color=red,
explicit(rhs(tangenta(f(x),x,0)),x,-4.5,4.5),color="#23ab0f", line_width=5,
parametric(0,t,t,-4,5),
color="blue",
point_type=filled_circle,point_size=1.5,
points([[0,f(0)]]),
color="black",
yrange=[-5,6],label(["y=-2",4,-1.8]),
label(["x=0",0.25,4.5])),wxplot_size=[700,700];
(%t27)
(Graphics)
(%o27)
(%i28) draw2d(terminal=wxt,user_preamble="set size ratio 1",
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-5,1,5],ytics=[-4,1,6],explicit(f(x),x,-5,5),line_width=2,color=red,
explicit(rhs(tangenta(f(x),x,0)),x,-4.5,4.5),color="#23ab0f", line_width=5,
parametric(0,t,t,-4,5),
color="blue",
point_type=filled_circle,point_size=1.5,
points([[0,f(0)]]),
color="black",
yrange=[-5,6],label(["y=-2",4,-1.8]),
label(["x=0",0.25,4.5]));
(%o28) [gr2d(explicit,explicit,parametric,points,label,label)]

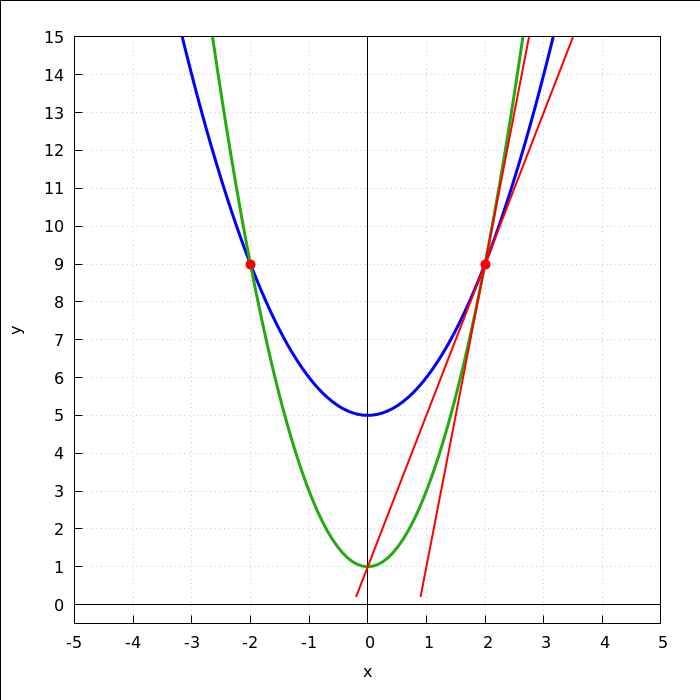
4. zadatak - kut između krivulja

definiramo funkciju koja će nam olakšati računanje kuta između krivulja

(%i29) kut_krivulja(fun1,fun2,x,x0):=block([k1:subst(x0,x,diff(fun1,x)),k2:subst(x0,x,diff(fun2,x))],
atan(abs(k1-k2)/(1+k1*k2)))$
(%i31) f1(x):=x^2+5;
f2(x):=2*x^2+1;
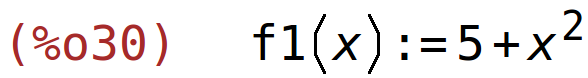
(%o30) f1(x):=5+x^2
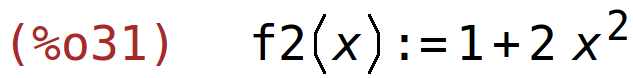
(%o31) f2(x):=1+2*x^2
(%i32) solve(f1(x)=f2(x),x);
(%o32) [x=-2,x=2]

kut između krivulja u točki presjeka u prvom kvadrantu

(%i33) kut_krivulja(f1(x),f2(x),x,2);
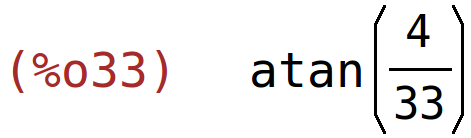
(%o33) atan(4/33)

kut između krivulja u točki presjeka u drugom kvadrantu

(%i34) kut_krivulja(f1(x),f2(x),x,-2);
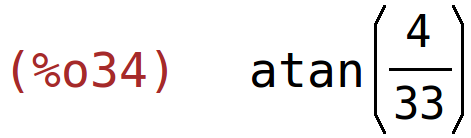
(%o34) atan(4/33)
(%i35) wxdraw2d(user_preamble="set size ratio 1",
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-5,1,5],ytics=[-1,1,15],
explicit(f1(x),x,-5,5),
color="#23ab0f",
explicit(f2(x),x,-5,5),
line_width=2,color=red,
explicit(rhs(tangenta(f2(x),x,2)),x,0.9,4.5),
explicit(rhs(tangenta(f1(x),x,2)),x,-0.2,4.5),
point_type=filled_circle,point_size=1.5,
points([[2,f1(2)],[-2,f1(-2)]]),
color="black",
yrange=[-0.5,15],label(["y=-2",4,-1.8])),wxplot_size=[700,700];
(%t35)
(Graphics)
(%o35)
(%i36) draw2d(terminal=wxt,user_preamble="set size ratio 1",
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-5,1,5],ytics=[-1,1,15],
explicit(f1(x),x,-5,5),
color="#23ab0f",
explicit(f2(x),x,-5,5),
line_width=2,color=red,
explicit(rhs(tangenta(f2(x),x,2)),x,0.9,4.5),
explicit(rhs(tangenta(f1(x),x,2)),x,-0.2,4.5),
point_type=filled_circle,point_size=1.5,
points([[2,f1(2)],[-2,f1(-2)]]),
color="black",
yrange=[-0.5,15],label(["y=-2",4,-1.8]));
(%o36) [gr2d(explicit,explicit,explicit,explicit,points,label)]

2 Ekstremi

1. zadatak

(%i37) f(x):=x*%e^(-x);
(%o37) f(x):=x*%e^(-x)

nultočke

(%i38) solve(x*%e^(-x)=0,x);
(%o38) [x=0]

lokalni ekstremi

(%i39) diff(f(x),x);
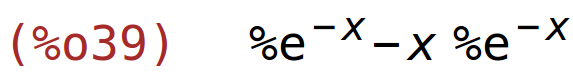
(%o39) %e^(-x)-x*%e^(-x)
(%i40) solve(%=0,x);
(%o40) [x=1]
(%i41) f(1);
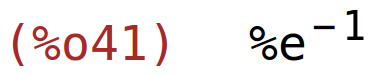
(%o41) %e^(-1)

radi se o lokalnom maksimumu jer je f''(1)<0

(%i42) subst(1,x,diff(f(x),x,2));
(%o42) -%e^(-1)

točke infleksije

(%i43) solve(diff(f(x),x,2)=0,x);
(%o43) [x=2]

y=0 je desna horizontalna asimptota (stoga funkcija nema desnu kosu asimptotu)

(%i44) limit(f(x),x,inf);
(%o44) 0

funkcija nema lijevu horizontalnu asimptotu, niti lijevu kosu asimptotu

(%i45) limit(f(x),x,minf);
(%o45) -inf
(%i46) limit(f(x)/x,x,minf);
(%o46) inf

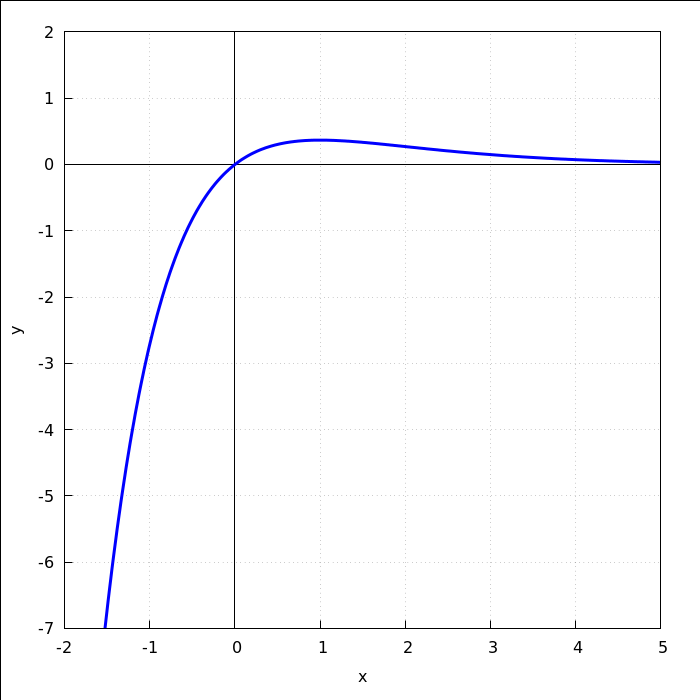
graf funkcije

(%i47) wxdraw2d(user_preamble="set size ratio 1",
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-5,1,5],ytics=[-10,1,2],
explicit(x*%e^(-x),x,-2,5),
yrange=[-7,2]),wxplot_size=[700,700];
(%t47)
(Graphics)
(%o47)
(%i48) draw2d(terminal=wxt,user_preamble="set size ratio 1",
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-5,1,5],ytics=[-10,1,2],
explicit(x*%e^(-x),x,-2,5),
yrange=[-7,2]);
(%o48) [gr2d(explicit)]

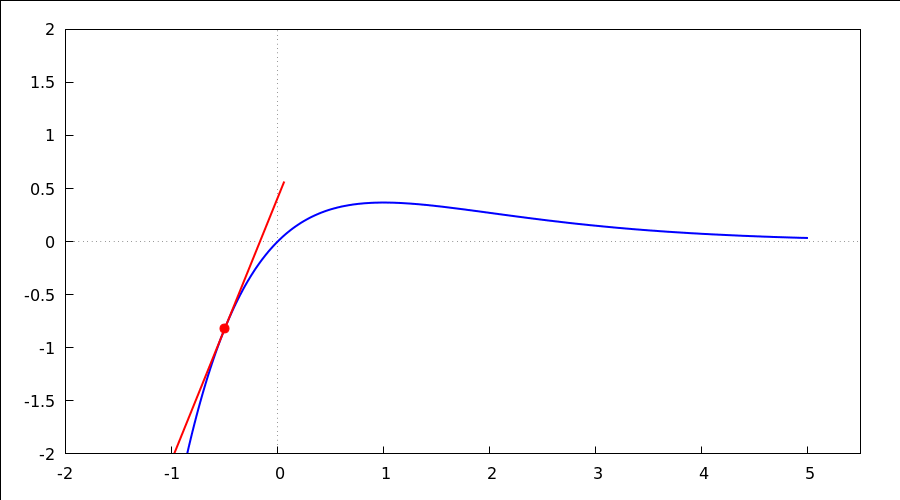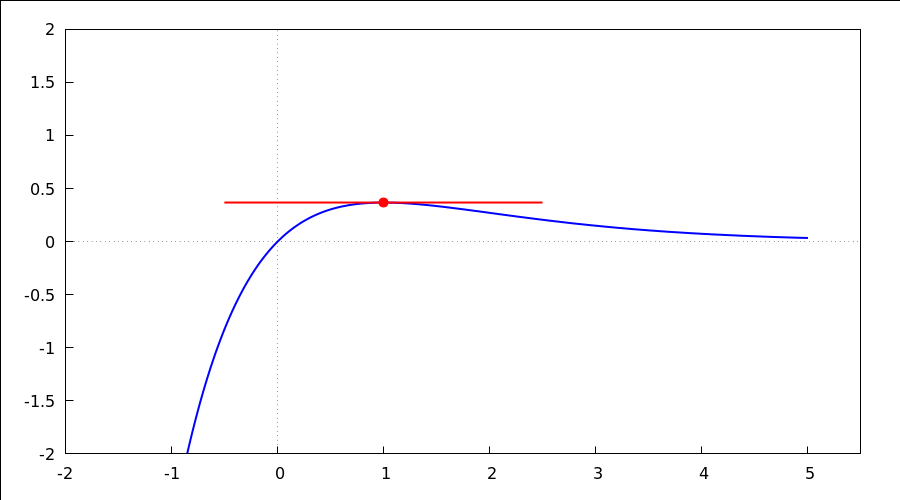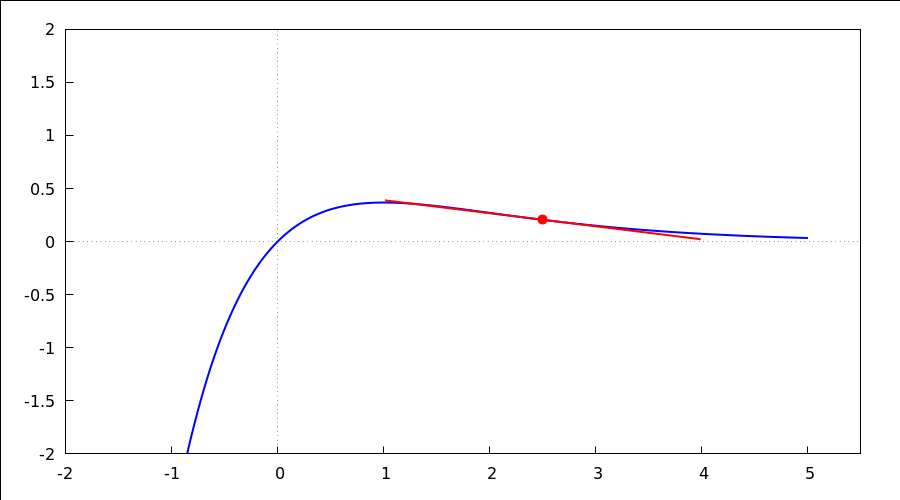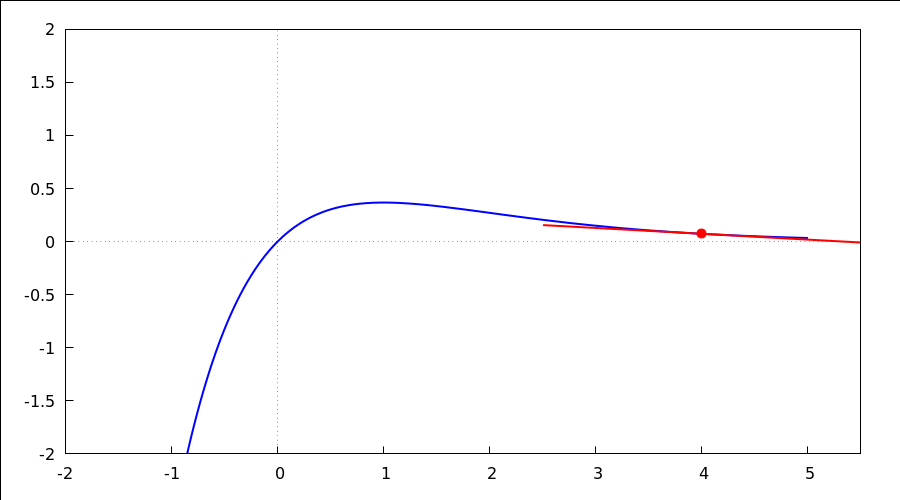
animacija tangente po grafu funkcije - uočite položaj tangente na graf funkcije
u konveksnom i konkavnom području, uočite točku infleksije;
kliknite na donju sliku i kotačićem na mišu možete mijenjati tangentu ili pak
pomoću tipki u toolbaru ("trokut", "kvadrat", "slider")

(%i49) with_slider_draw(
  x0, makelist(-0.5+0.25*dx,dx,0,18),
  proportional_axes = xy,
  line_width = 2,
  color = blue,
      explicit(x*%e^(-x), x, -2, 5),
  color = red,
  point_type=filled_circle,
  point_size=1.5,
  points([[x0,x0*%e^(-x0)]]),
  points_joined = true,
  point_size=0,
  points([[x0,x0*%e^(-x0)]-1.5/sqrt(1+(1-x0)^2*%e^(-2*x0))*[1,(1-x0)*%e^(-x0)],
  [x0,x0*%e^(-x0)]+1.5/sqrt(1+(1-x0)^2*%e^(-2*x0))*[1,(1-x0)*%e^(-x0)]]),
  dimensions=[900,500],
  yrange = [-2, 2],
  xrange = [-2, 5.5],
  xaxis = true,
  yaxis = true
)$
(%t49)
Animated Diagram

2. zadatak

(%i50) g(x):=x*%e^(-x^2);
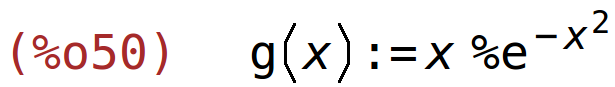
(%o50) g(x):=x*%e^(-x^2)

nultočke

(%i51) solve(g(x)=0,x);
(%o51) [x=0]

kandidati za lokalne ekstreme - stacionarne točke

(%i52) diff(g(x),x);
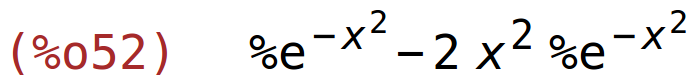
(%o52) %e^(-x^2)-2*x^2*%e^(-x^2)
(%i53) factor(%);
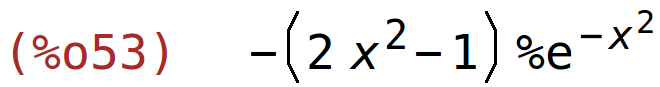
(%o53) -(2*x^2-1)*%e^(-x^2)
(%i54) solve(%=0,x);
(%o54) [x=-1/sqrt(2),x=1/sqrt(2)]

ispitivanje stacionarnih točaka

(%i55) diff(g(x),x,2);
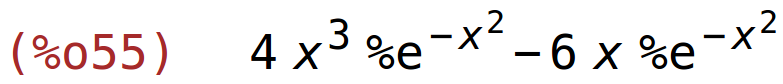
(%o55) 4*x^3*%e^(-x^2)-6*x*%e^(-x^2)
(%i56) g2:factor(%);
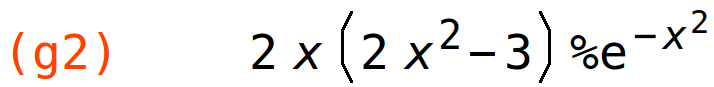
(g2) 2*x*(2*x^2-3)*%e^(-x^2)

lokalni minimum

(%i57) subst(-1/sqrt(2),x,g2);
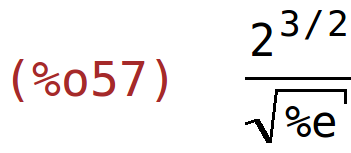
(%o57) 2^(3/2)/sqrt(%e)
(%i58) g(-1/sqrt(2));
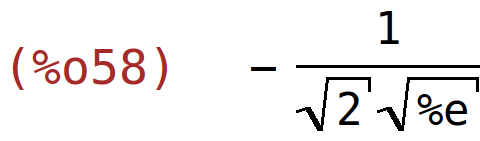
(%o58) -1/(sqrt(2)*sqrt(%e))
(%i59) g(-1/sqrt(2)),numer;
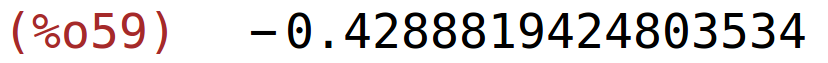
(%o59) -0.4288819424803534

lokalni maksimum

(%i60) subst(1/sqrt(2),x,g2);
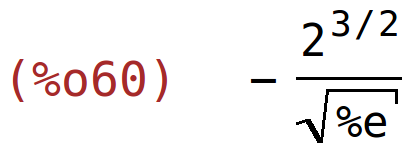
(%o60) -2^(3/2)/sqrt(%e)
(%i61) g(1/sqrt(2));
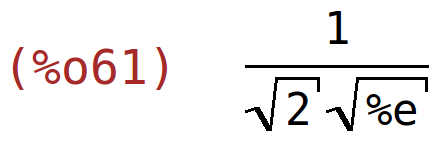
(%o61) 1/(sqrt(2)*sqrt(%e))
(%i62) g(1/sqrt(2)),numer;
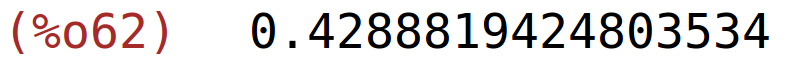
(%o62) 0.4288819424803534

točke infleksije

(%i63) solve(g2=0,x);
(%o63) [x=-sqrt(3)/sqrt(2),x=sqrt(3)/sqrt(2),x=0]

y=0 je lijeva i desna horizontalna asimptota (dakle, nema kosih asimptoti)

(%i64) limit(g(x),x,inf);
(%o64) 0
(%i65) limit(g(x),x,minf);
(%o65) 0

graf funkcije

(%i66) wxplot2d(x*%e^(-x^2), [x,-3,3],[y,-1,1])$
(%t66)
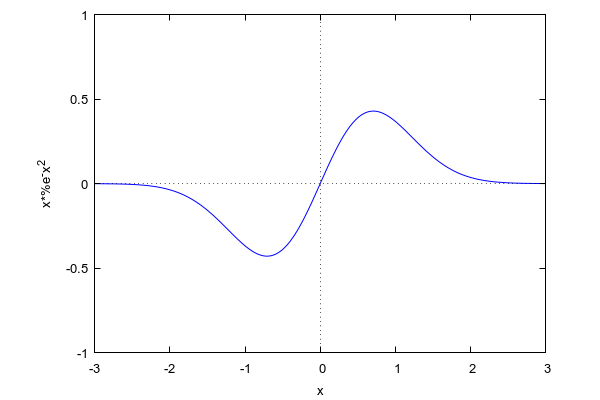
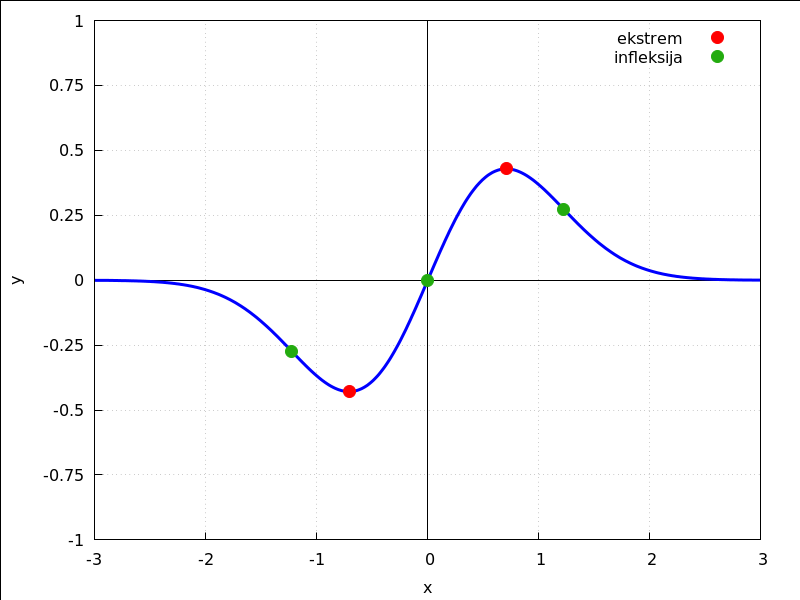
(Graphics)

ili malo bolja i detaljnija slika

(%i67) wxdraw2d(grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-3,1,3],ytics=[-1,0.25,1],
explicit(x*%e^(-x^2),x,-3,3),
point_size=2,color=red,point_type=filled_circle,
key="ekstrem",
points([[-1/sqrt(2),g(-1/sqrt(2))],[1/sqrt(2),g(1/sqrt(2))]]),
color="#23ab0f",key="infleksija",
points([[0,0],[sqrt(3/2),g(sqrt(3/2))],[-sqrt(3/2),g(-sqrt(3/2))]]),
xrange=[-3,3],
yrange=[-1,1]),wxplot_size=[800,600];
(%t67)
(Graphics)
(%o67)
(%i68) draw2d(terminal=wxt,
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-3,1,3],ytics=[-1,0.25,1],
explicit(x*%e^(-x^2),x,-3,3),
point_size=2,color=red,point_type=filled_circle,
key="ekstrem",
points([[-1/sqrt(2),g(-1/sqrt(2))],[1/sqrt(2),g(1/sqrt(2))]]),
color="#23ab0f",key="infleksija",
points([[0,0],[sqrt(3/2),g(sqrt(3/2))],[-sqrt(3/2),g(-sqrt(3/2))]]),
xrange=[-3,3],
yrange=[-1,1]);
(%o68) [gr2d(explicit,points,points)]

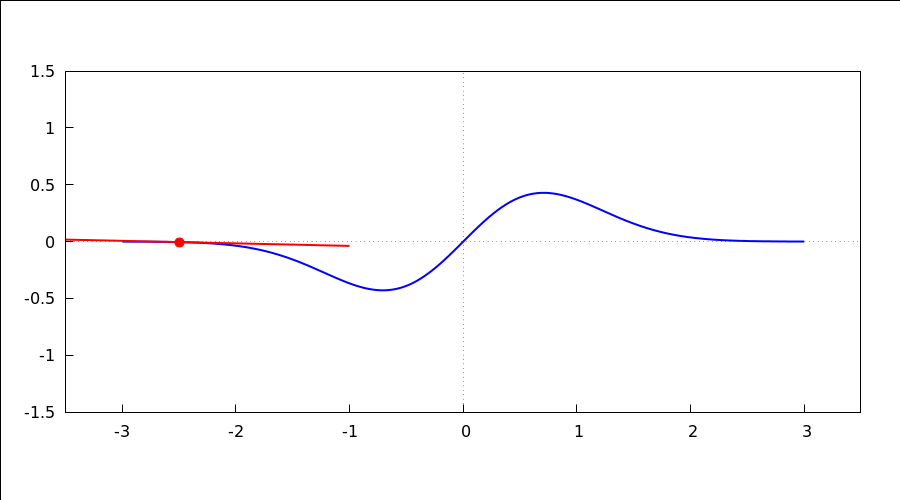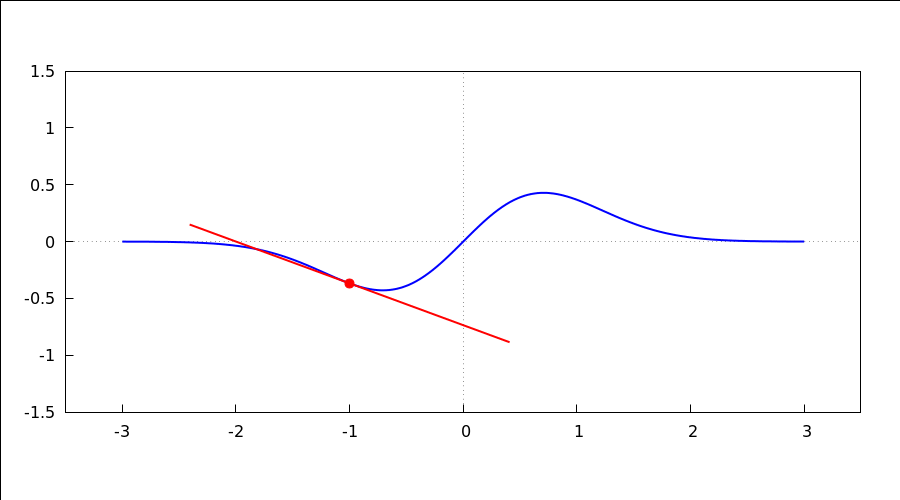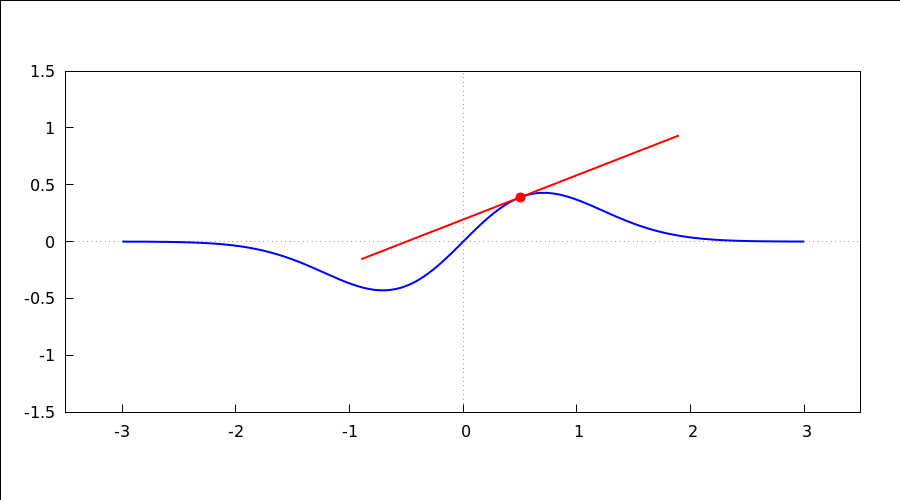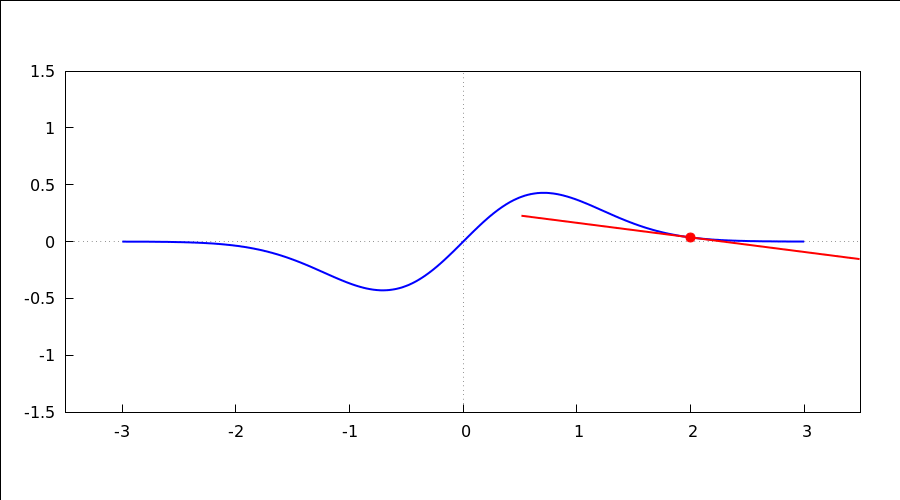
animacija kretanja tangente po grafu funkcije

(%i69) with_slider_draw(
  x0, makelist(-2.5+0.25*dx,dx,0,18),
  proportional_axes = xy,
  line_width = 2,
  color = blue,
      explicit(x*%e^(-x^2), x, -3, 3),
  color = red,
  point_type=filled_circle,
  point_size=1.5,
  points([[x0,x0*%e^(-x0^2)]]),
  points_joined = true,
  point_size=0,
  points([[x0,x0*%e^(-x0^2)]-1.5/sqrt(1+(1-2*x0^2)^2*%e^(-2*x0^2))*[1,(1-2*x0^2)*%e^(-x0^2)],
  [x0,x0*%e^(-x0^2)]+1.5/sqrt(1+(1-2*x0^2)^2*%e^(-2*x0^2))*[1,(1-2*x0^2)*%e^(-x0^2)]]),
  dimensions=[900,500],
  yrange = [-1.5, 1.5],
  xrange = [-3.5, 3.5],
  xaxis = true,
  yaxis = true
)$
(%t69)
Animated Diagram

3. zadatak

(%i70) h(x):=(x-4)/(3*x-x^2);
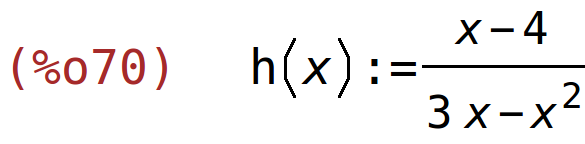
(%o70) h(x):=(x-4)/(3*x-x^2)

nultočke

(%i71) solve(h(x)=0,x);
(%o71) [x=4]

kandidati za lokalne ekstreme - stacionarne točke

(%i72) diff(h(x),x);
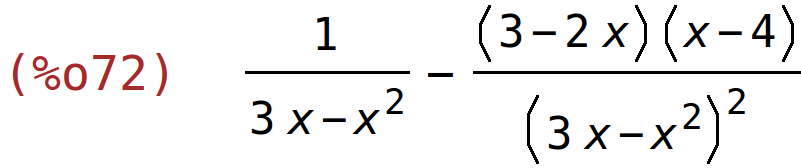
(%o72) 1/(3*x-x^2)-((3-2*x)*(x-4))/(3*x-x^2)^2
(%i73) ratsimp(%);
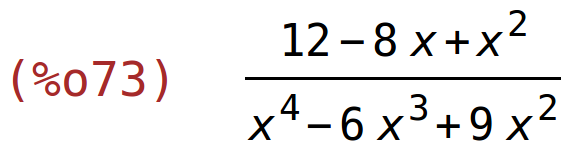
(%o73) (12-8*x+x^2)/(x^4-6*x^3+9*x^2)
(%i74) solve(%=0,x);
(%o74) [x=6,x=2]

ispitivanje stacionarnih točaka

(%i75) h2:ratsimp(diff(h(x),x,2));
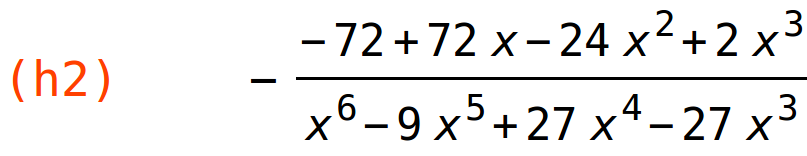
(h2) -(-72+72*x-24*x^2+2*x^3)/(x^6-9*x^5+27*x^4-27*x^3)

lokalni minimum

(%i76) subst(6,x,h2);
(%o76) 1/81
(%i77) h(6);
(%o77) -1/9

lokalni maksimum

(%i78) subst(2,x,h2);
(%o78) -1
(%i79) h(2);
(%o79) -1

točke infleksije - samo je jedna (prva dva rješenja su kompleksni brojevi)

(%i80) solve(h2=0,x);
(%o80) [x=2^(2/3)*((sqrt(3)*%i)/2-1/2)+2^(4/3)*(-1/2-(sqrt(3)*%i)/2)+4,x=2^(4/3)*((sqrt(3)*%i)/2-1/2)+2^(2/3)*(-1/2-(sqrt(3)*%i)/2)+4,x=2^(4/3)+2^(2/3)+4]
(%i81) 2^(4/3)+2^(2/3)+4,numer;
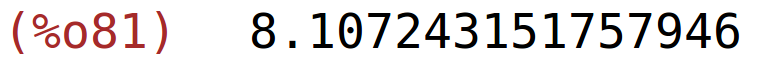
(%o81) 8.107243151757946

x=0 i x=3 su (lijeve i desne) vertikalne asimptote

(%i82) limit(h(x),x,0,plus);
(%o82) -inf
(%i83) limit(h(x),x,0,minus);
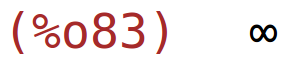
(%o83) inf
(%i84) limit(h(x),x,3,plus);
(%o84) inf
(%i85) limit(h(x),x,3,minus);
(%o85) -inf

y=0 je (lijeva i desna) horizontalna asimptota. Dakle, nema kosih asimptoti.

(%i86) limit(h(x),x,inf);
(%o86) 0
(%i87) limit(h(x),x,minf);
(%o87) 0

graf funkcije

(%i88) wxplot2d([(x-4)/(3*x-x^2)], [x,-5,5],[y,-20,20],
[gnuplot_preamble,"set xtics (-4,-3,-2,-1,0,1,2,3,4)"])$
plot2d: expression evaluates to non-numeric value somewhere in plotting range.plot2d: some values were clipped.<BR>
(%t88)
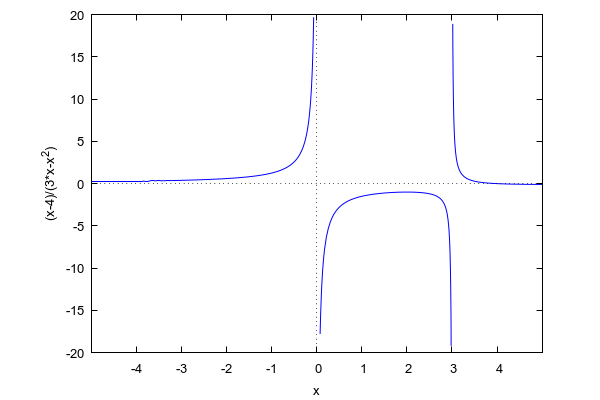
(Graphics)

malo detaljnija slika

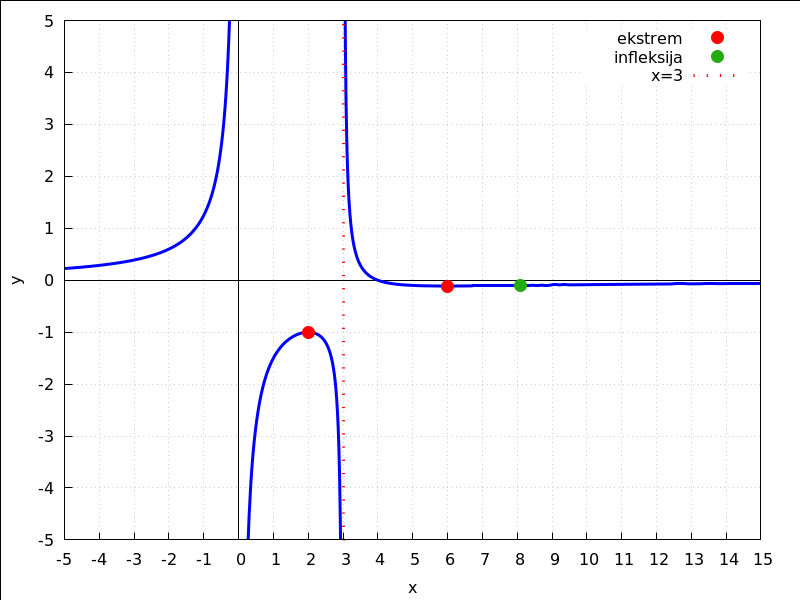
(%i89) wxdraw2d(grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-5,1,15],ytics=[-5,1,5],
explicit((x-4)/(3*x-x^2),x,-5,15),
point_size=2,color=red,point_type=filled_circle,
key="ekstrem",
points([[6,-1/9],[2,-1]]),
color="#23ab0f",key="infleksija",
points([[2^(4/3)+2^(2/3)+4,h(2^(4/3)+2^(2/3)+4)]]),
line_width=3,color=red,key="x=3",line_type=dots,
parametric(3,t,t,-5,5),
xrange=[-5,15],
yrange=[-5,5]),wxplot_size=[800,600];
(%t89)
(Graphics)
(%o89)
(%i90) draw2d(terminal=wxt,
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-5,1,15],ytics=[-5,1,5],
explicit((x-4)/(3*x-x^2),x,-5,15),
point_size=2,color=red,point_type=filled_circle,
key="ekstrem",
points([[6,-1/9],[2,-1]]),
color="#23ab0f",key="infleksija",
points([[2^(4/3)+2^(2/3)+4,h(2^(4/3)+2^(2/3)+4)]]),
line_width=3,color=red,key="x=3",line_type=dots,
parametric(3,t,t,-5,5),
xrange=[-5,15],
yrange=[-5,5]);
(%o90) [gr2d(explicit,points,points,parametric)]

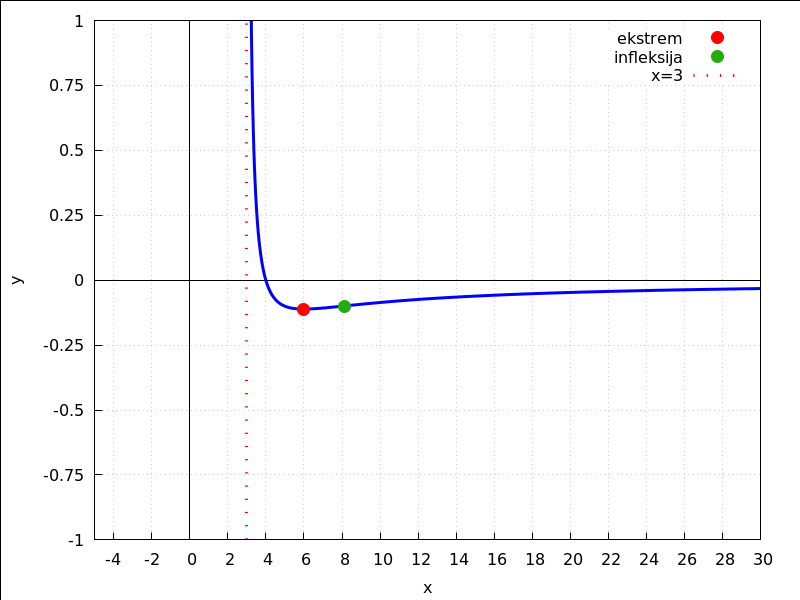
SLIKA NAS PONEKAD MOŽE PREVARITI. Zato je na donjoj slici nacrtan graf promatrane funkcije
samo na dijelu domene x>3 kako bi se jasnije vidio lokalni minimum u točki x=6 i kako bi se
jasnije vidjela točka infleksije.

(%i91) wxdraw2d(grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-4,2,30],ytics=[-1.5,0.25,1.5],
explicit((x-4)/(3*x-x^2),x,3.1,30),
point_size=2,color=red,point_type=filled_circle,
key="ekstrem",
points([[6,-1/9]]),
color="#23ab0f",key="infleksija",
points([[2^(4/3)+2^(2/3)+4,h(2^(4/3)+2^(2/3)+4)]]),
line_width=3,color=red,key="x=3",line_type=dots,
parametric(3,t,t,-5,5),
xrange=[-5,30],
yrange=[-1,1]),wxplot_size=[800,600];
(%t91)
(Graphics)
(%o91)
(%i92) draw2d(terminal=wxt,
grid=true,xaxis=true,xaxis_width=1,xaxis_type=solid,xlabel="x",
yaxis=true,yaxis_width=1,yaxis_type=solid,ylabel="y",line_width=3,color=blue,
xtics=[-5,1,30],ytics=[-1.5,0.25,1.5],
explicit((x-4)/(3*x-x^2),x,3.1,30),
point_size=2,color=red,point_type=filled_circle,
key="ekstrem",
points([[6,-1/9]]),
color="#23ab0f",key="infleksija",
points([[2^(4/3)+2^(2/3)+4,h(2^(4/3)+2^(2/3)+4)]]),
line_width=3,color=red,key="x=3",line_type=dots,
parametric(3,t,t,-5,5),
xrange=[-5,30],
yrange=[-1,1]);
(%o92) [gr2d(explicit,points,points,parametric)]

4. zadatak

(%i93) k(x):=(2*x^2-8)/(5*x);
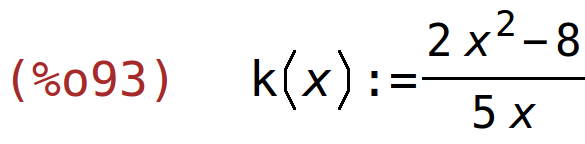
(%o93) k(x):=(2*x^2-8)/(5*x)

nultočke

(%i94) solve(k(x)=0,x);
(%o94) [x=-2,x=2]

nema lokalnih ekstrema (nema realnih rješenja)

(%i95) diff(k(x),x);
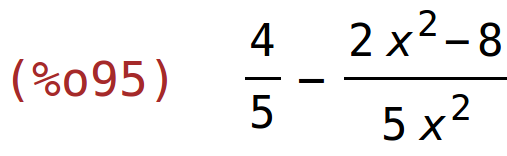
(%o95) 4/5-(2*x^2-8)/(5*x^2)
(%i96) ratsimp(%);
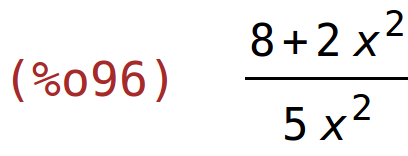
(%o96) (8+2*x^2)/(5*x^2)
(%i97) solve(%=0,x);
(%o97) [x=-2*%i,x=2*%i]

nema točaka infleksije (to ne mora značiti da je funkcija na svojoj prirodnoj domeni
uvijek konveksna ili konkavna)

(%i98) diff(k(x),x,2);
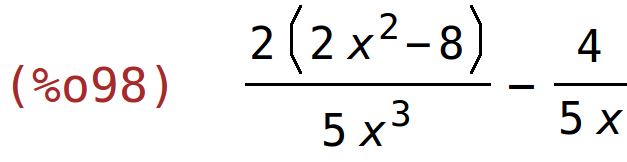
(%o98) (2*(2*x^2-8))/(5*x^3)-4/(5*x)
(%i99) ratsimp(%);
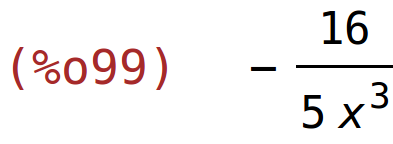
(%o99) -16/(5*x^3)

x=0 je (lijeva i desna) vertikalna asimptota

(%i100) limit(k(x),x,0,plus);
(%o100) -inf
(%i101) limit(k(x),x,0,minus);
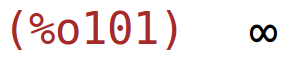
(%o101) inf

nema horizontalnih asimptota

(%i102) limit(k(x),x,inf);
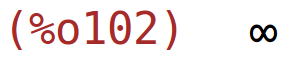
(%o102) inf
(%i103) limit(k(x),x,minf);
(%o103) -inf

pravac y=2/5*x je (lijeva i desna) kosa asimptota

(%i104) limit(k(x)/x,x,inf);
(%o104) 2/5
(%i105) limit(k(x)-2/5*x,x,inf);
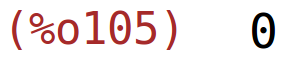
(%o105) 0
(%i106) limit(k(x)/x,x,minf);
(%o106) 2/5
(%i107) limit(k(x)-2/5*x,x,minf);
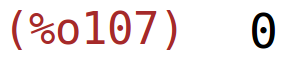
(%o107) 0

graf funkcije

(%i108) wxplot2d([(2*x^2-8)/(5*x),2/5*x],[x,-10,10],[y,-20,20],
  [gnuplot_preamble, "set grid;"],[style,[lines,2,1],[points,0.5,2,6]]),wxplot_size=[800,600]$
plot2d: expression evaluates to non-numeric value somewhere in plotting range.plot2d: some values were clipped.<BR>
(%t108)
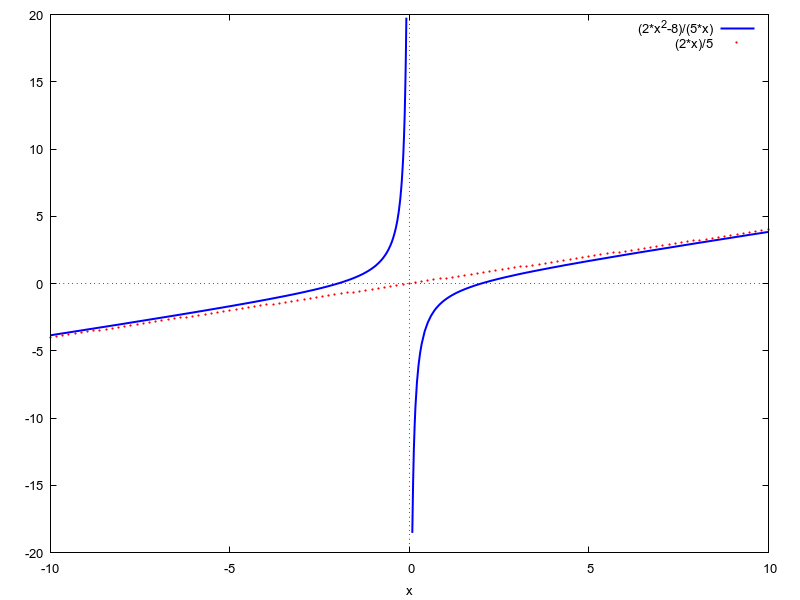
(Graphics)
(%i109) plot2d([(2*x^2-8)/(5*x),2/5*x],[x,-10,10],[y,-20,20],[gnuplot_term,wxt],
      [gnuplot_preamble, "set grid;"],[style,[lines,2,1],[points,1,2,8]])$
plot2d: expression evaluates to non-numeric value somewhere in plotting range.plot2d: some values were clipped.<BR>
Created with wxMaxima.