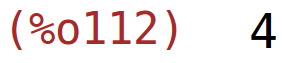1 Generiranje matrice

Generiranje matrice čiji elementi su zadani nekom formulom

(%i1) T: genmatrix(lambda([i,j],i-j), 5,4);
(T) matrix(<BR> [0, -1, -2, -3],<BR> [1, 0, -1, -2],<BR> [2, 1, 0, -1],<BR> [3, 2, 1, 0],<BR> [4, 3, 2, 1]<BR> )
(%i2) M: genmatrix(lambda([i,j], if i>j then cos(i*%pi/2) else log(i+j)/log(2)), 3, 4);
(M) matrix(<BR> [1, log(3)/log(2), log(4)/log(2), log(5)/log(2)],<BR> [-1, log(4)/log(2), log(5)/log(2), log(6)/log(2)],<BR> [0, 0, log(6)/log(2), log(7)/log(2)]<BR> )

2 Operacije s matricama

1. zadatak

(%i3) A: matrix(
[1,2],
[0,-3],
[5,4]
);
(A) matrix(<BR> [1, 2],<BR> [0, -3],<BR> [5, 4]<BR> )
(%i4) B:matrix(
[1,0,-2,5],
[8,4,-1,3]
);
(B) matrix(<BR> [1, 0, -2, 5],<BR> [8, 4, -1, 3]<BR> )
(%i5) A.B;
(%o5) matrix(<BR> [17, 8, -4, 11],<BR> [-24, -12, 3, -9],<BR> [37, 16, -14, 37]<BR> )
(%i6) B.A;
MULTIPLYMATRICES: attempt to multiply nonconformable matrices. -- an error. To debug this try: debugmode(true);<BR>
(%i7) transpose(A);
(%o7) matrix(<BR> [1, 0, 5],<BR> [2, -3, 4]<BR> )

2. zadatak

(%i8) A: matrix(
[3,1,-4],
[-4,6,-2],
[5,8,5]
);
(A) matrix(<BR> [3, 1, -4],<BR> [-4, 6, -2],<BR> [5, 8, 5]<BR> )
(%i9) B: matrix(
[3,7,-4],
[2,1,0],
[-5,3,2]
);
(B) matrix(<BR> [3, 7, -4],<BR> [2, 1, 0],<BR> [-5, 3, 2]<BR> )
(%i10) A.B;
(%o10) matrix(<BR> [31, 10, -20],<BR> [10, -28, 12],<BR> [6, 58, -10]<BR> )
(%i11) B.A;
(%o11) matrix(<BR> [-39, 13, -46],<BR> [2, 8, -10],<BR> [-17, 29, 24]<BR> )
(%i12) 3*A.B-7*B.A;
(%o12) matrix(<BR> [366, -61, 262],<BR> [16, -140, 106],<BR> [137, -29, -198]<BR> )

3. zadatak

(%i13) A: matrix([3,-2],[-1,5]);
(A) matrix(<BR> [3, -2],<BR> [-1, 5]<BR> )
(%i14) A^^2;
(%o14) matrix(<BR> [11, -16],<BR> [-8, 27]<BR> )
(%i15) A^^3;
(%o15) matrix(<BR> [49, -102],<BR> [-51, 151]<BR> )
(%i16) diag_matrix(1,1);
(%o16) matrix(<BR> [1, 0],<BR> [0, 1]<BR> )
(%i17) A^^3+2*A^^2+3*diag_matrix(1,1);
(%o17) matrix(<BR> [74, -134],<BR> [-67, 208]<BR> )

Oprez. Uočite razliku između sljedećih operacija

(%i18) A: matrix([3,1,-4],[-4,6,-2],[5,8,5]);
(A) matrix(<BR> [3, 1, -4],<BR> [-4, 6, -2],<BR> [5, 8, 5]<BR> )
(%i19) B: matrix([3,7,-4],[2,1,0],[-5,3,2]);
(B) matrix(<BR> [3, 7, -4],<BR> [2, 1, 0],<BR> [-5, 3, 2]<BR> )

Oprez: * (zvjezdica) samo množi matrice po pozicijama

(%i20) A*B;
(%o20) matrix(<BR> [9, 7, 16],<BR> [-8, 6, 0],<BR> [-25, 24, 10]<BR> )
(%i21) B*A;
(%o21) matrix(<BR> [9, 7, 16],<BR> [-8, 6, 0],<BR> [-25, 24, 10]<BR> )

Pomoću . (točkica) maxima vrši pravo množenje matrica

(%i22) A.B;
(%o22) matrix(<BR> [31, 10, -20],<BR> [10, -28, 12],<BR> [6, 58, -10]<BR> )
(%i23) B.A;
(%o23) matrix(<BR> [-39, 13, -46],<BR> [2, 8, -10],<BR> [-17, 29, 24]<BR> )

Oprez: ^ samo potencira matrice po elementima

(%i24) A^2;
(%o24) matrix(<BR> [9, 1, 16],<BR> [16, 36, 4],<BR> [25, 64, 25]<BR> )

^^ obavlja pravo potenciranje matrica

(%i25) A^^2;
(%o25) matrix(<BR> [-15, -23, -34],<BR> [-46, 16, -6],<BR> [8, 93, -11]<BR> )

ako ne želimo ispisati matrice

(%i26) A: matrix([3,1,-4],[-4,6,-2],[5,8,5])$
(%i27) B: matrix([3,7,-4],[2,1,0],[-5,3,2])$

4. zadatak

(%i29) A: matrix([2,-2,0],[1,-2,1])$
B: matrix([2],[1],[3])$
(%i30) A.B;
(%o30) matrix(<BR> [2],<BR> [3]<BR> )

5. zadatak

(%i32) A: matrix([2,3],[1,5])$
B: 9/5*matrix([1,0,4],[3,6,8])$
(%i33) A.B;
(%o33) matrix(<BR> [99/5, 162/5, 288/5],<BR> [144/5, 54, 396/5]<BR> )

3 Determinante

1. zadatak

(%i36) A: matrix([2,5],[1,-3]);
B: matrix([x-a,-a],[a,x+a]);
C: matrix([sin(a),cos(a)],[sin(b),cos(b)]);
(A) matrix(<BR> [2, 5],<BR> [1, -3]<BR> )
(B) matrix(<BR> [x-a, -a],<BR> [a, x+a]<BR> )
(C) matrix(<BR> [sin(a), cos(a)],<BR> [sin(b), cos(b)]<BR> )
(%i37) determinant(A);
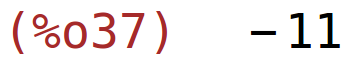
(%o37) -11
(%i38) determinant(B);
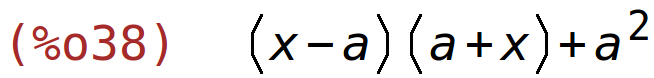
(%o38) (x-a)*(a+x)+a^2
(%i39) expand(determinant(B));
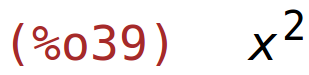
(%o39) x^2
(%i40) determinant(C);
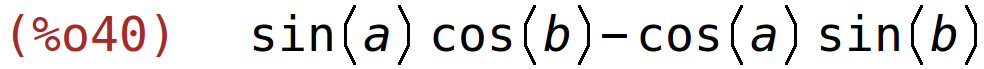
(%o40) sin(a)*cos(b)-cos(a)*sin(b)
(%i41) trigreduce(determinant(C));
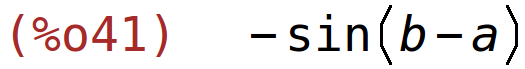
(%o41) -sin(b-a)

možemo i direktno izračunati determinatu bez spremanja matrice u varijablu

(%i42) determinant(matrix([2,5],[1,-3]));
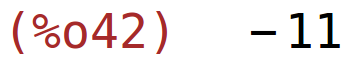
(%o42) -11

2. zadatak

(%i43) A: matrix([9,4,-5],[8,7,-2],[2,-1,8])$
(%i44) determinant(A);
(%o44) 324

3. zadatak

(%i45) A: matrix([2,-5,1,2],[-3,7,-1,4],[5,-9,2,7],[4,-6,1,2])$
(%i46) determinant(A);
(%o46) -9

4. zadatak

(%i47) A: matrix([3,a,3,a],[6,3,6,3],[7,7,6,6],[a,5,a,5])$
(%i48) determinant(A);
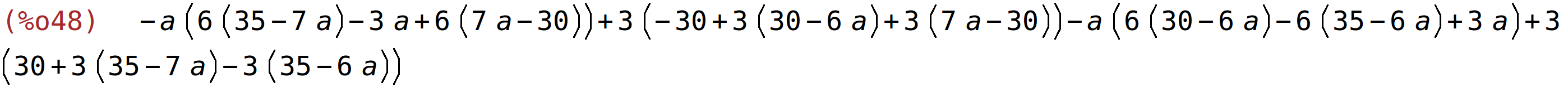
(%o48) -a*(6*(35-7*a)-3*a+6*(7*a-30))+3*(-30+3*(30-6*a)+3*(7*a-30))-a*(6*(30-6*a)-6*(35-6*a)+3*a)+3*(30+3*(35-7*a)-3*(35-6*a))
(%i49) expand(determinant(A));
(%o49) 0

mogli smo determinantu spremiti u neku varijablu i zatim pojednostavniti taj izraz

(%i50) izraz: determinant(A);
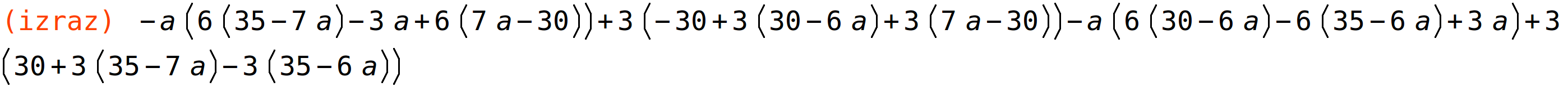
(izraz) -a*(6*(35-7*a)-3*a+6*(7*a-30))+3*(-30+3*(30-6*a)+3*(7*a-30))-a*(6*(30-6*a)-6*(35-6*a)+3*a)+3*(30+3*(35-7*a)-3*(35-6*a))
(%i51) expand(izraz);
(%o51) 0

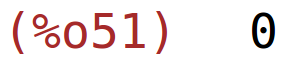
5. zadatak

(%i52) A: matrix([a,a,a,a,a],[-2,a,a,a,a],[2,0,a,a,a],[-4,0,0,a,a],[4,0,0,0,a])$
(%i53) determinant(A);
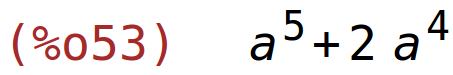
(%o53) a^5+2*a^4

6. zadatak

(%i54) A: matrix([4+x,2,2],[7,x-1,2],[x+1,5,5]);
(A) matrix(<BR> [x+4, 2, 2],<BR> [7, x-1, 2],<BR> [x+1, 5, 5]<BR> )
(%i55) det: determinant(A);
(det) 2*(35-(x-1)*(1+x))-2*(35-2*(1+x))+(5*(x-1)-10)*(4+x)

pojednostavljenje izraza za determinantu

(%i56) expand(det);
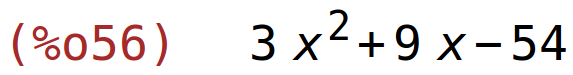
(%o56) 3*x^2+9*x-54

rješavanje jednadžbe det(A)=0

(%i57) solve(expand(det)=0,x);
(%o57) [x=3,x=-6]

računanje izraza det(A^T)+5*det(A^3)-2*det(1/2*A) za x=-1

(%i58) rezultat2: determinant(transpose(A))+5*determinant(A^^3)-2*determinant(1/2*A);
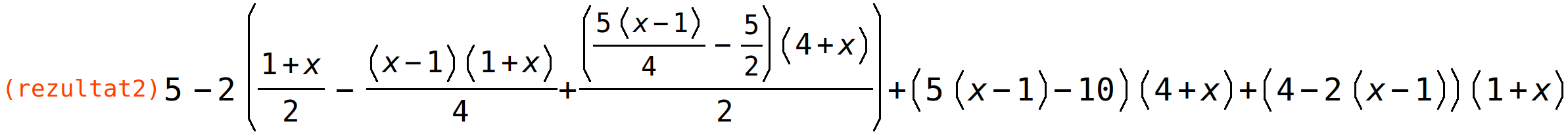
(rezultat2) 5*-2*((1+x)/2-((x-1)*(1+x))/4+(((5*(x-1))/4-5/2)*(4+x))/2)+(5*(x-1)-10)*(4+x)+(4-2*(x-1))*(1+x)
(%i59) expand(rezultat2);
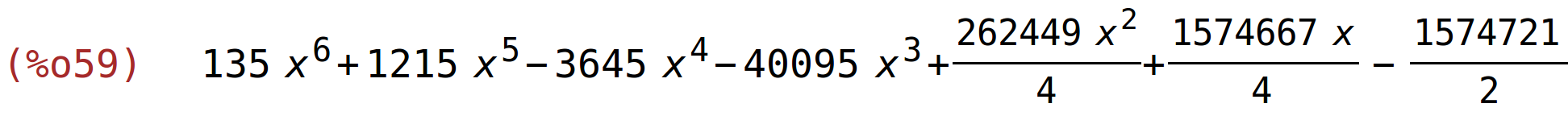
(%o59) 135*x^6+1215*x^5-3645*x^4-40095*x^3+(262449*x^2)/4+(1574667*x)/4-1574721/2
(%i60) subst(-1,x,expand(rezultat2));
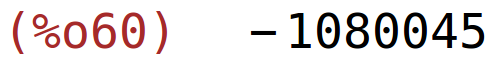
(%o60) -1080045

mogli smo najprije x=-1 uvrstiti u matricu A kako smo to radili i na seminarima

(%i61) B: subst(-1,x,A);
(B) matrix(<BR> [3, 2, 2],<BR> [7, -2, 2],<BR> [0, 5, 5]<BR> )
(%i62) determinant(transpose(B))+5*determinant(B^^3)-2*determinant(1/2*B);
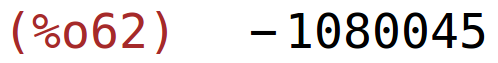
(%o62) -1080045

7. zadatak

(%i63) A: matrix([x-3,3,3,3],[3,2*x+3,3,3],[3,3,x-3,3],[3,3,3,2*x+3]);
(A) matrix(<BR> [x-3, 3, 3, 3],<BR> [3, 2*x+3, 3, 3],<BR> [3, 3, x-3, 3],<BR> [3, 3, 3, 2*x+3]<BR> )
(%i64) determinant(A);
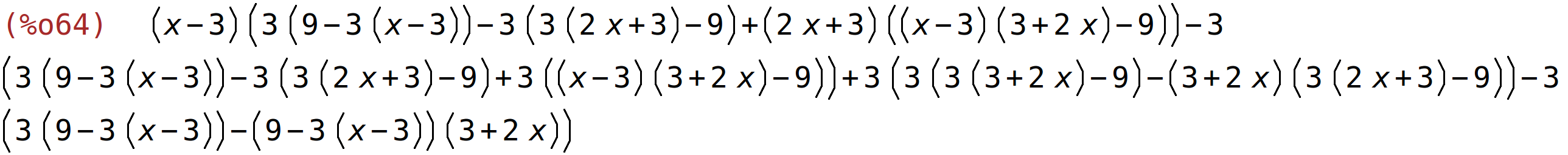
(%o64) (x-3)*(3*(9-3*(x-3))-3*(3*(2*x+3)-9)+(2*x+3)*((x-3)*(3+2*x)-9))-3*(3*(9-3*(x-3))-3*(3*(2*x+3)-9)+3*((x-3)*(3+2*x)-9))+3*(3*(3*(3+2*x)-9)-(3+2*x)*(3*(2*x+3)-9))-3*(3*(9-3*(x-3))-(9-3*(x-3))*(3+2*x))
(%i65) izraz: expand(determinant(A));
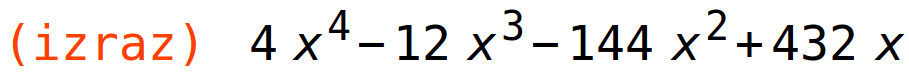
(izraz) 4*x^4-12*x^3-144*x^2+432*x
(%i66) solve(izraz=0,x);
(%o66) [x=3,x=-6,x=6,x=0]

4 Inverzna matrica

1. zadatak

(%i67) A: matrix([2,1],[-5,4]);
(A) matrix(<BR> [2, 1],<BR> [-5, 4]<BR> )

dva načina traženja inverza matrice

(%i68) invert(A);
(%o68) matrix(<BR> [4/13, -1/13],<BR> [5/13, 2/13]<BR> )
(%i69) A^^-1;
(%o69) matrix(<BR> [4/13, -1/13],<BR> [5/13, 2/13]<BR> )

Oprez: Dolje navedena naredba samo daje matricu inverznih elemenata, a ne inverznu matricu matrice A

(%i70) A^-1;
(%o70) matrix(<BR> [1/2, 1],<BR> [-1/5, 1/4]<BR> )

želimo li kod invertiranja matrice determinantu izlučiti izvan matrice

(%i74) detout: true$
doallmxops: false$
doscmxops: false$
invert(A);
(%o74) matrix(<BR> [4, -1],<BR> [5, 2]<BR> )/13

jednom kad smo varijablu detout postavili na true, tada samo mijenjanjem vrijednosti varijable doallmxops prelazimo iz jednog u drugi način pisanja inverza matrice

(%i75) doallmxops: true$
(%i76) invert(A);
(%o76) matrix(<BR> [4/13, -1/13],<BR> [5/13, 2/13]<BR> )

mogli smo i jednostavnije izlučiti determinantu izvan inverzne matrice tako da posebno odredimo adjunktu, a posebno determinantu

(%i77) adjoint(A);
(%o77) matrix(<BR> [4, -1],<BR> [5, 2]<BR> )
(%i78) determinant(A);
(%o78) 13

2. zadatak

(%i79) B: 2/3*matrix([3,5],[1,-3]);
(B) matrix(<BR> [2, 10/3],<BR> [2/3, -2]<BR> )
(%i80) B^^-1;
(%o80) matrix(<BR> [9/28, 15/28],<BR> [3/28, -9/28]<BR> )

3. zadatak

(%i81) E: matrix([-3,4,-5],[4,-3,2],[1,-3,4]);
(E) matrix(<BR> [-3, 4, -5],<BR> [4, -3, 2],<BR> [1, -3, 4]<BR> )
(%i82) invert(E);
(%o82) matrix(<BR> [-6/7, -1/7, -1],<BR> [-2, -1, -2],<BR> [-9/7, -5/7, -1]<BR> )
(%i84) doallmxops: false$
invert(E);
(%o84) matrix(<BR> [-6, -1, -7],<BR> [-14, -7, -14],<BR> [-9, -5, -7]<BR> )/7

adjunkta i determinanta

(%i85) adjoint(E);
(%o85) matrix(<BR> [-6, -1, -7],<BR> [-14, -7, -14],<BR> [-9, -5, -7]<BR> )
(%i86) determinant(E);
(%o86) 7

4. zadatak

(%i87) A: 5/3*matrix([1,5,8],[2,3,-1],[4,-5,-9]);
(A) (5*matrix(<BR> [1, 5, 8],<BR> [2, 3, -1],<BR> [4, -5, -9]<BR> ))/3

problem???

(%i88) invert(A);
not a matrix: (5*matrix(<BR> [1, 5, 8],<BR> [2, 3, -1],<BR> [4, -5, -9]<BR> ))/3 -- an error. To debug this try: debugmode(true);<BR>

rješenje problema: treba barem jednu od varijabli doallmxops ili doscmxops postaviti na true

(%i90) doscmxops: true$
A: 5/3*matrix([1,5,8],[2,3,-1],[4,-5,-9]);
(A) matrix(<BR> [5/3, 25/3, 40/3],<BR> [10/3, 5, -5/3],<BR> [20/3, -25/3, -15]<BR> )
(%i91) invert(A);
(%o91) matrix(<BR> [16/115, -1/46, 29/230],<BR> [-7/115, 41/230, -17/230],<BR> [11/115, -5/46, 7/230]<BR> )

želimo li determinatu izlučiti izvan matrice tada moramo varijablu doscmxops postaviti na false (jer smo ju maloprije gore postavili na true)

(%i93) doscmxops: false$
invert(A);
(%o93) -(9*matrix(<BR> [-800/9, 125/9, -725/9],<BR> [350/9, -1025/9, 425/9],<BR> [-550/9, 625/9, -175/9]<BR> ))/5750
(%i94) doallmxops: true$

5. zadatak

(%i95) [A: matrix([a,1,-1],[-1,1,1],[-2,0,0]),B: matrix([1,0,0],[0,a^2-1,1],[b,0,1])];
(%o95) [matrix(<BR> [a, 1, -1],<BR> [-1, 1, 1],<BR> [-2, 0, 0]<BR> ),matrix(<BR> [1, 0, 0],<BR> [0, a^2-1, 1],<BR> [b, 0, 1]<BR> )]
(%i96) determinant(A);
(%o96) -4
(%i97) determinant(B);
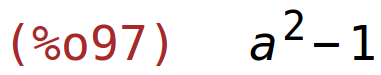
(%o97) a^2-1
(%i98) determinant(A.B);
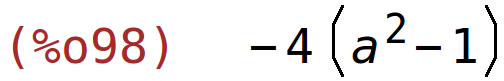
(%o98) -4*(a^2-1)
(%i99) solve(determinant(A.B)=0,a);
(%o99) [a=-1,a=1]

6. zadatak

(%i100) A: matrix([0,1,-1,4],[2,1,0,1],[3,2,2,5],[-2,-4,-1,1]);
(A) matrix(<BR> [0, 1, -1, 4],<BR> [2, 1, 0, 1],<BR> [3, 2, 2, 5],<BR> [-2, -4, -1, 1]<BR> )
(%i101) invert(A);
(%o101) matrix(<BR> [-13/82, 53/82, -1/41, 9/82],<BR> [15/82, -17/82, -2/41, -23/82],<BR> [-23/82, -45/82, 14/41, -3/82],<BR> [11/82, -7/82, 4/41, 5/82]<BR> )
(%i103) doallmxops: false$
invert(A);
(%o103) -matrix(<BR> [13, -53, 2, -9],<BR> [-15, 17, 4, 23],<BR> [23, 45, -28, 3],<BR> [-11, 7, -8, -5]<BR> )/82
(%i104) doallmxops: true$

adjunkta i determinanta

(%i105) adjoint(A);
(%o105) matrix(<BR> [13, -53, 2, -9],<BR> [-15, 17, 4, 23],<BR> [23, 45, -28, 3],<BR> [-11, 7, -8, -5]<BR> )
(%i106) determinant(A);
(%o106) -82

5 Rang matrice

(%i107) A: matrix([2,6,-4,1,2],[4,-12,8,0,-4],[-3,9,2,-2,3]);
(A) matrix(<BR> [2, 6, -4, 1, 2],<BR> [4, -12, 8, 0, -4],<BR> [-3, 9, 2, -2, 3]<BR> )
(%i108) rank(A);
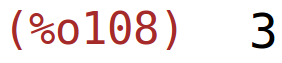
(%o108) 3
(%i109) B: matrix([1,-2,0,4,3,0],[-2,0,5,2,6,1],[0,1,1,3,-2,-1],[-1,-2,5,6,9,1],[1,0,2,10,-1,-2]);
(B) matrix(<BR> [1, -2, 0, 4, 3, 0],<BR> [-2, 0, 5, 2, 6, 1],<BR> [0, 1, 1, 3, -2, -1],<BR> [-1, -2, 5, 6, 9, 1],<BR> [1, 0, 2, 10, -1, -2]<BR> )
(%i110) rank(B);
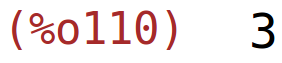
(%o110) 3
(%i111) C: matrix([3,2,0,1],[1,-1,1,1],[4,2,-1,1],[0,0,2,1]);
(C) matrix(<BR> [3, 2, 0, 1],<BR> [1, -1, 1, 1],<BR> [4, 2, -1, 1],<BR> [0, 0, 2, 1]<BR> )
(%i112) rank(C);
(%o112) 4
Created with wxMaxima.