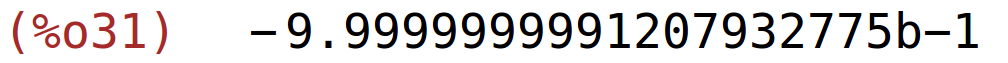1 Numeričko traženje nultočki funkcije
| (%i1) | f(x):=x*sin(x)+1; |
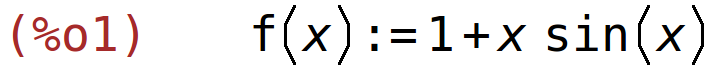
| (%i2) |
wxplot2d([x*sin(x)+1], [x,0,10], grid2d, [xtics,0,1,10], [ytics,-6,1,10], [yx_ratio,-1], [axes,solid], [legend,false], [style,[lines,2]]), wxplot_size=[500,600]; |
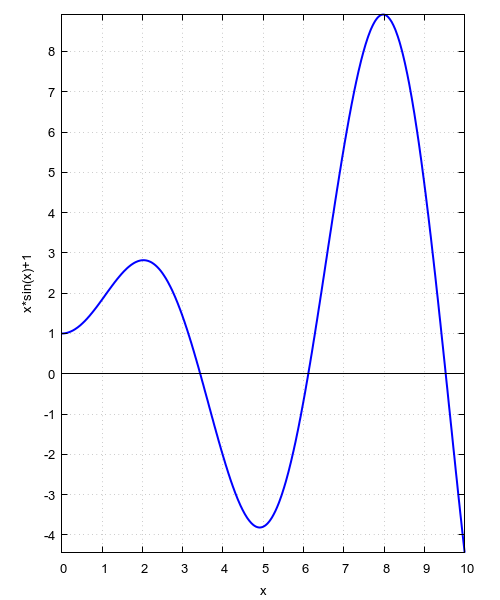

neka nultočka na segmentu [0,10]
| (%i3) | find_root(f,0,10); |
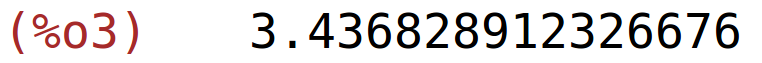
| (%i4) | find_root(x*sin(x)+1,x,0,10); |
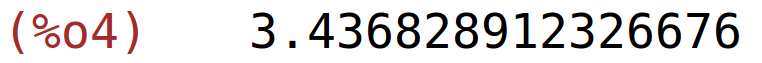
ako želimo nultočku na segmentu [9,10]
| (%i5) | find_root(f,9,10); |

| (%i6) | find_root(x*sin(x)+1,x,9,10); |
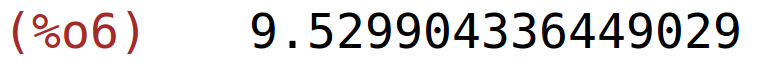
ako želimo nultočku na segmentu [6,7]
| (%i7) | find_root(f,6,7); |
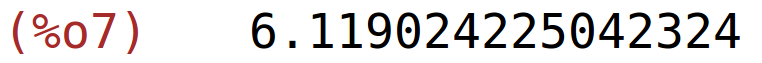
| (%i8) | find_root(x*sin(x)+1,x,6,7); |
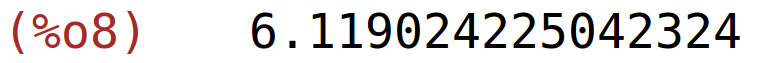
možemo staviti npr. segment [5.5,6.5] za nultočku između brojeva 6 i 7
| (%i9) | find_root(f,5.5,6.5); |
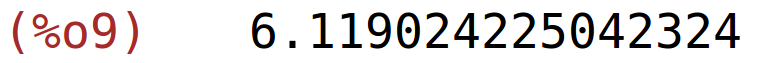
| (%i10) | find_root(x*sin(x)+1,x,5.5,6.5); |
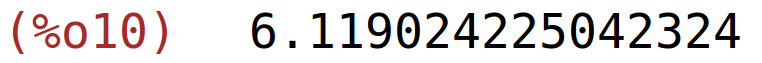
segment [3,7] nije dobar u ovom slučaju jer ne vrijedi uvjet f(3)*f(7)<0
| (%i11) | find_root(x*sin(x)+1,x,3,7); |
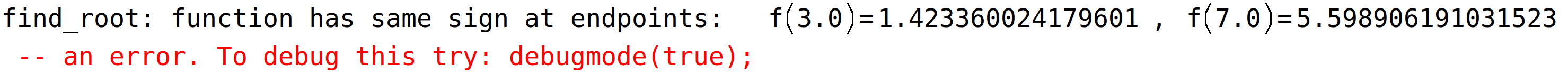
Želimo li veću preciznost, koristimo naredbu bf_find_root i varijablu fpprec za broj znamenki
| (%i12) | bf_find_root(f,6,7), fpprec:50; |
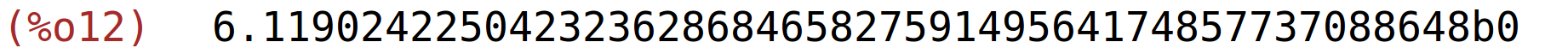
2 Presjek grafova
| (%i13) | f(x); |
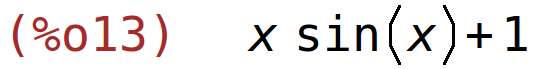
| (%i14) | g(x):=cos(x); |
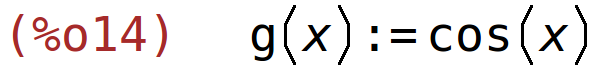
| (%i15) |
wxplot2d([f(x),g(x)], [x,0,10], grid2d, [xtics,0,1,10], [ytics,-6,1,10], [yx_ratio,-1], [axes,solid], [legend,false], [style,[lines,2],[lines,2]]), wxplot_size=[500,600]; |

točka presjeka (x1,y1) na segmentu [3,4]
| (%i17) |
x1:find_root(f(x)=g(x),x,3,4); y1:f(x1); |
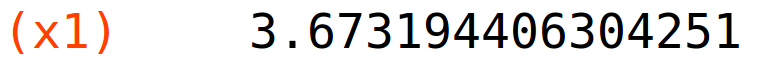
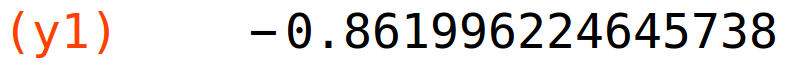
točka presjeka (x2,y2) na segmentu [6,7]
| (%i19) |
x2:find_root(f(x)=g(x),x,6,7); y2:f(x2); |
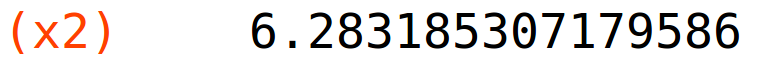
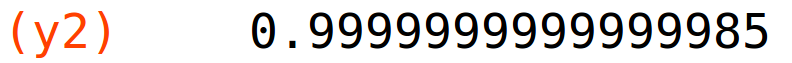
točka presjeka (x3,y3) na segmentu [9,10]
| (%i21) |
x3:find_root(f(x)=g(x),x,9,10); y3:f(x3); |
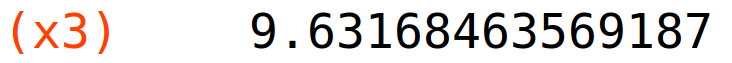
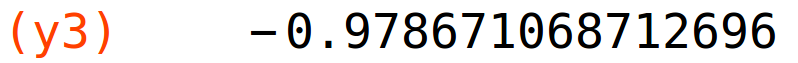
3 Kada naredba find_root neće pronaći nultočku
| (%i22) | f(x):=(x+1)*sin(x+1); |
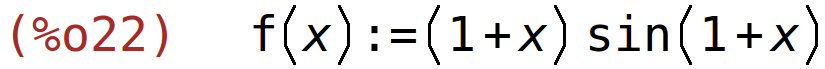
| (%i23) |
wxplot2d([f(x),0,[parametric,0,t,[t,-1.5,2]]], [x,-5,3], [y,-1.5,2], grid2d, [xtics,-5,1,2], [ytics,-1.5,0.5,2], [yx_ratio,1], [axes,solid], [legend,false], [style,[lines,2],[lines,1,2],[lines,1,2]]), wxplot_size=[600,600]; |

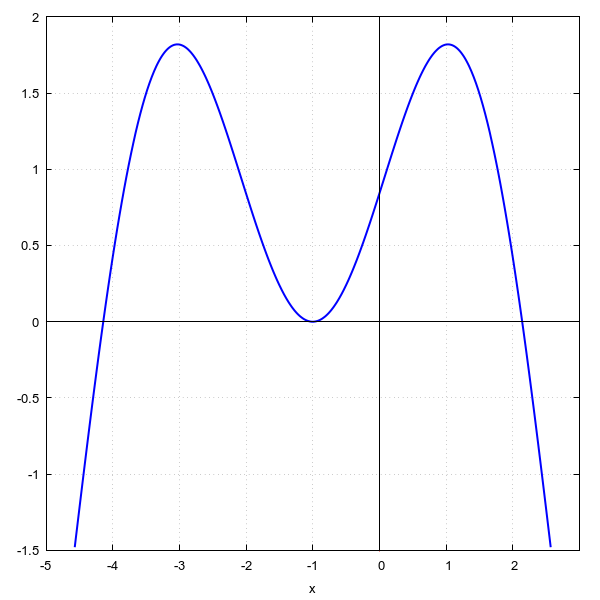

Ne postoji segment [a,b] koji bi sadržavao samo nultočku -1 i za kojeg bi vrijedilo f(a)*f(b)<0.
Stoga naredba find_root neće moći nikako detektirati nultočku -1.
za segment [-2,0] nije zadovoljen uvjet f(-2)*f(0)<0
| (%i24) | find_root(f,-2,0); |

segment [-2,3] ne sadrži samo nultočku -1, a find_root naredba daje drugu nultočku unutar segmenta [-2,3]
| (%i25) | find_root(f,-2,3); |
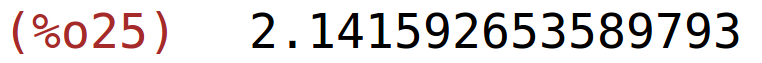
3.1 Naredba newton
Pomoću naredbe newton možemo locirati tu nultočku jer ta naredba ne zahtijeva da specificiramo na početku segment, nego samo jednu točku od koje želimo početi tražiti neku nultočku.
| (%i26) | load(newton1); |
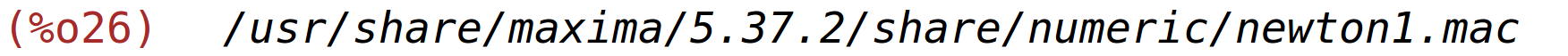
Nultočku počinjemo tražiti od točke 0 tako dugo dok vrijednost funkcije nije manja od 10^(-15).
Dobivamo aproksimaciju nultočke -1.
| (%i27) | newton(f(x),x,0,10^(-15)); |

Nultočku počinjemo tražiti od točke -2 tako dugo dok vrijednost funkcije nije manja od 10^(-15).
Dobivamo aproksimaciju nultočke -1.
| (%i28) | newton(f(x),x,-2,10^(-15)); |
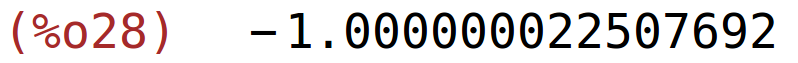
Nultočku počinjemo tražiti od točke 2 tako dugo dok vrijednost funkcije nije manja od 10^(-15).
Ne dobivamo aproksimaciju nultočke -1, već neku drugu nultočku jer smo počeli od točke koja
je bliža ovoj drugoj nultočki.
| (%i29) | newton(f(x),x,2.5,10^(-15)); |
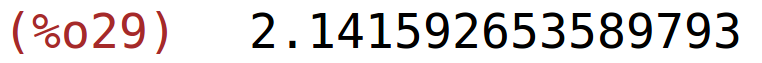
za veću preciznost moramo se prebaciti na aritmetiku velike preciznosti, npr. na 20 znamenki
| (%i30) | newton(bfloat(f(x)),x,2.5,bfloat(10^(-20))), fpprec:20; |
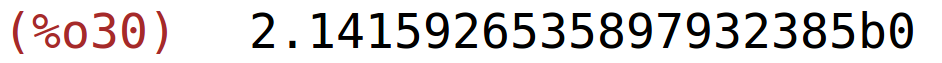
| (%i31) | newton(bfloat(f(x)),x,0,bfloat(10^(-20))), fpprec:20; |