osnove

1 Osnovne računske operacije u maximi

(%i1)

3+5;

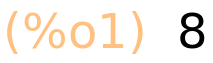
(%i2)

6/5−7/15;

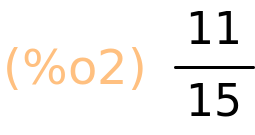
(%i3)

(2+5)/(18−4·9);

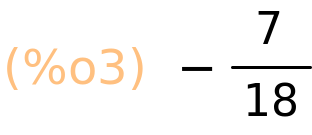
potenciranje

(%i4)

2^5;

(%i5)

5^20;

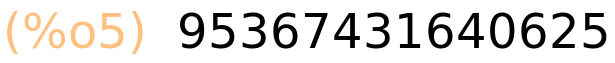
(%i6)

(7/15)^10;

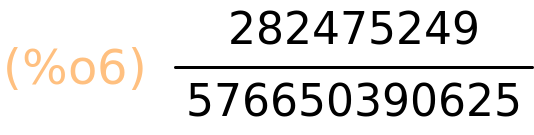
korjenovanje ide preko potencija

(%i7)

4^(2/3);

(%i8)

sqrt(5);

pretvaranje broja u decimalni zapis

(%i9)

11/15;

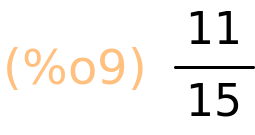
(%i10)

11/15,numer;

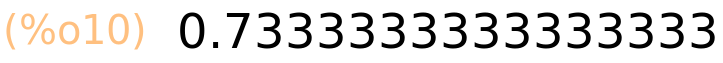
(%i11)

float(11/15);

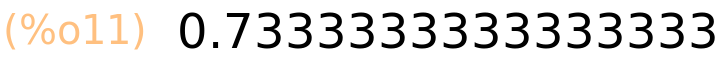
(%i12)

11/15.0;

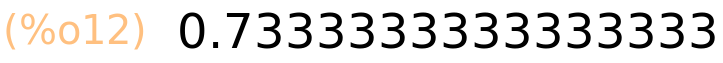
(%i13)

11.0/15;

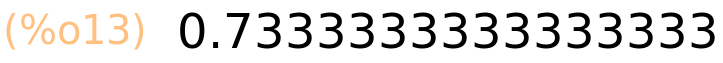
(%i14)

11.0/15.0;

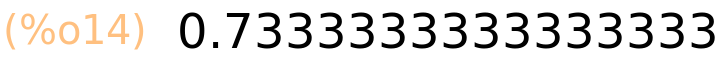
(%i15)

4^(2/3),numer;

(%i16)

float(4^(2/3));

(%i17)

4.0^(2/3);

(%i18)

sqrt(5),numer;

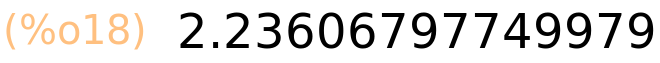
(%i19)

sqrt(5.0);

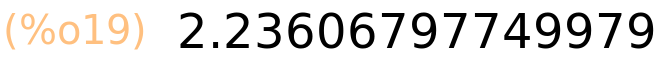
možemo brzo sve elemente matrice pretvoriti u decimalne brojeve

(%i20)

A:matrix([1/2,3^(2/5)],[5/6,1]);

(A) matrix(<BR>
[1/2, 3^(2/5)],<BR>
[5/6, 1]<BR>
)

(%i21)

A1:A,numer;

(A1) matrix(<BR>
[0.5, 1.55184557391536],<BR>
[0.8333333333333334, 1]<BR>
)

(%i22)

A1;

(%o22) matrix(<BR>
[0.5, 1.55184557391536],<BR>
[0.8333333333333334, 1]<BR>
)

(%i23)

float(A);

(%o23) matrix(<BR>
[0.5, 1.55184557391536],<BR>
[0.8333333333333334, 1.0]<BR>
)

2 Broj pi i broj e

(%i24)

%pi;

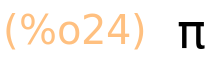
(%i25)

%e;

(%i26)

%pi,numer;

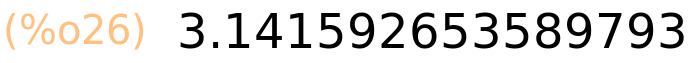
(%i27)

float(%pi);

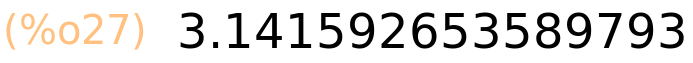
(%i28)

%e,numer;

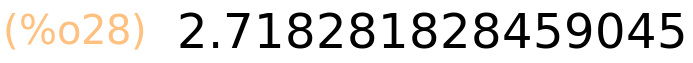
(%i29)

float(%e);

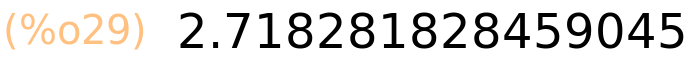
3 Dobivanje brojeva s većom preciznošću

(%i30)

bfloat(%pi),fpprec:50;

(%o30) 3.1415926535897932384626433832795028841971693993751b0

preciznost je samo trenutno stavljena na 100 znamenaka

(%i31)

bfloat(%pi),fpprec:100;

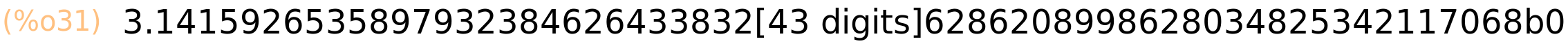
(%o31) 3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068b0

(%i32)

bfloat(%pi);

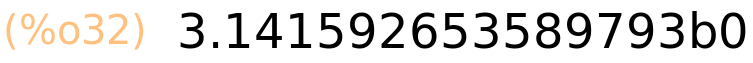
ako želimo da nam se ispišu sve znamenke

(%i33)

set_display(ascii);

(%i34)

bfloat(%pi),fpprec:100;

$(%o34) 3.141592653589793238462643383279502884197169399375105820974944592307816\ 406286208998628034825342117068b0$

preciznost je gloabalno stavljena na 100 znamenaka tako dugo dok ju opet globalno ne promijenimo

(%i35)

fpprec:100;

broj pi na 100 znamenaka (zadnja dva znaka "b0" znače da treba množiti s 10^0, tj. s 1)

(%i36)

bfloat(%pi);

$(%o36) 3.141592653589793238462643383279502884197169399375105820974944592307816\ 406286208998628034825342117068b0$

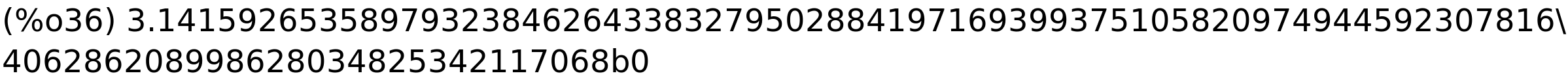
broj e na 100 znamenaka

(%i37)

bfloat(%e);

$(%o37) 2.718281828459045235360287471352662497757247093699959574966967627724076\ 630353547594571382178525166427b0$

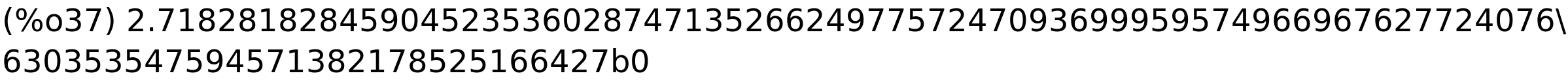
drugi korijen iz 2 na 100 znamenaka

(%i38)

bfloat(sqrt(2));

$(%o38) 1.414213562373095048801688724209698078569671875376948073176679737990732\ 478462107038850387534327641573b0$

treći korijen iz 5 na 100 znamenaka

(%i39)

bfloat(5^(1/3));

$(%o39) 1.709975946676696989353108872543860109868055110543054924382861707444295\ 920504173216257187010020189002b0$

vraćanje preciznosti na defaultnu vrijednost

(%i40)

fpprec:16;

vraćanje na standardni ispis

(%i41)

set_display(xml);

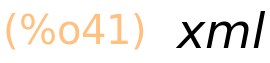
Pogledajmo detaljnije značenje slova b na kraju kod brojeva.

Na primjer, 100b2 zapravo znači 100*10^2 i to je broj 10000

(%i42)

100b2;

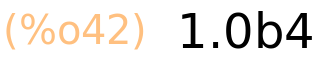
(%i43)

100b2,numer;

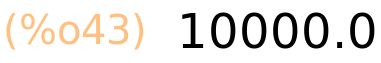
(%i44)

25.34b2;

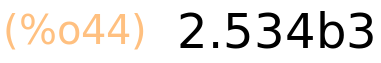
(%i45)

25.34b2,numer;

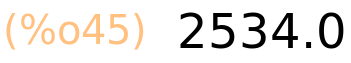
(%i46)

25.34b−4;

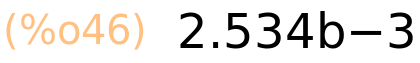
(%i47)

25.34b−4,numer;

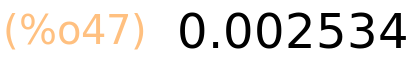
Kako brzo unijeti broj 45*10^20;

(%i48)

45b20;

(%i49)

45b20,numer;

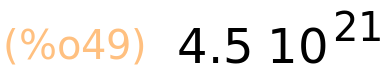
(%i50)

45b20+3b21;

4 Trigonometrijske funkcije

sinus

(%i51)

sin(2);

(%i52)

sin(2.0);

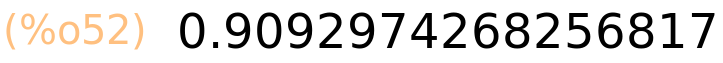
(%i53)

bfloat(sin(2.0)),fpprec:50;

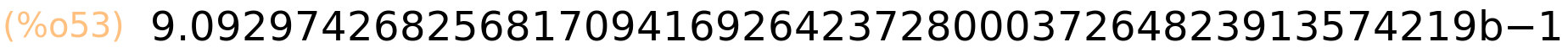
(%o53) 9.0929742682568170941692642372800037264823913574219b-1

(%i54)

sin(%pi);

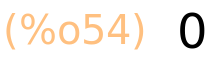
(%i55)

sin(%pi/2);

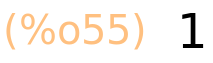
(%i56)

sin(3·%pi/2);

kosinus

(%i57)

cos(2);

(%i58)

cos(2.0);

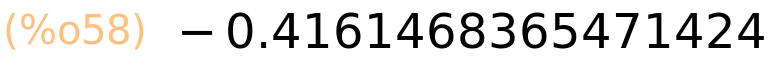
(%i59)

bfloat(cos(2.0)),fpprec:50;

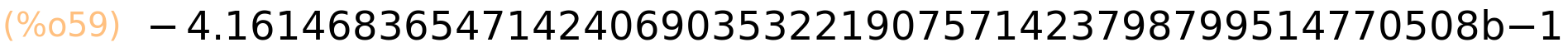
(%o59) -4.1614683654714240690353221907571423798799514770508b-1

(%i60)

cos(%pi);

(%i61)

cos(3·%pi/4);

tangens

(%i62)

tan(2);

(%i63)

tan(2.0);

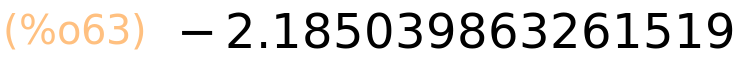
(%i64)

tan(%pi/4);

tangens od pi/2 ne postoji

(%i65)

tan(%pi/2);

kotangens

(%i66)

cot(2);

(%i67)

cot(2.0);

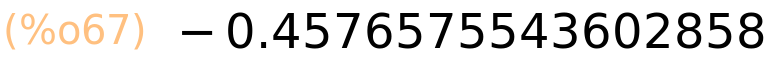
(%i68)

cot(%pi/2);

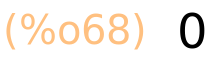
kotangens od pi ne postoji

(%i69)

cot(%pi);

tan: (3*%pi)/2 isn't in the domain of tan.<BR>
-- an error. To debug this try: debugmode(true);

jedan kompliciraniji izraz za izračunati

(%i70)

2·sin(2.0)+3/4·cos(2.0^(1/3))−tan(0.5);

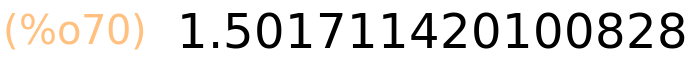
5 Logaritamska funkcija

Jako važno: u maximi log predstavlja logaritam po bazi e, a ne po bazi 10.

Dakle, u maximi je log=ln.

(%i71)

log(%e);

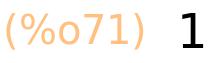
kako izračunati logaritam po bazi 2 od 5

(%i72)

log(5.0)/log(2.0);

kako izračunati logaritam po bazi 10 od 5

(%i73)

log(5.0)/log(10.0);

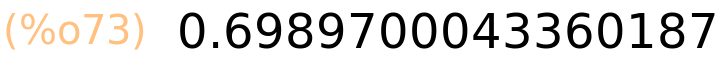
6 Spremanje objekata u varijablu

(%i75)

a:7;
b:8;

(%i76)

(%i77)

(%i78)

a^2+b^2;

(%i79)

sqrt(a^2+b^2);

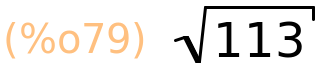
Ukoliko želimo da maxima zaboravi vrijednost neke varijable

(%i80)

kill(a);

(%i81)

a^2+b^2;

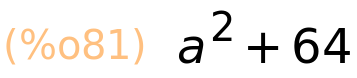
U varijablu možemo spremiti takoreći bilo što: broj, neki izraz, matricu,...

(%i82)

izraz:x^2+5·x+3;

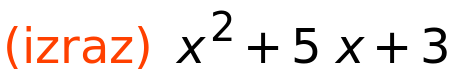
(%i83)

izraz+5·y;

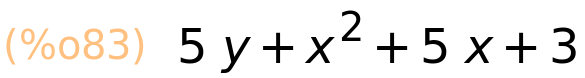
7 Određivanje kvocijenta i ostatka

7 pri dijeljenju s 5 daje kvocijent 1 i ostatak 2

(%i84)

mod(7,5);

(%i85)

quotient(7,5);

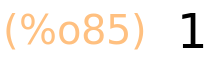
10237 pri dijeljenju s 543 daje kvocijent 18 i ostatak 463

(%i86)

mod(10237,543);

(%i87)

quotient(10237,543);

2^31 pri dijeljenju s 12 daje ostatak 8

(%i88)

mod(2^31,12);

power_mod je efikasnija naredba za veće potencije

(%i89)

power_mod(2,31,12);

možemo čak odjedanput odrediti ostatke pri dijeljenju nekim brojem svih elemenata matrice

(%i90)

B:matrix([34,21],[12,58]);

(B) matrix(<BR>
[34, 21],<BR>
[12, 58]<BR>
)

ostaci pri dijeljenju brojem 7 elemenata u matrici

(%i91)

mod(B,7);

(%o91) matrix(<BR>
[6, 0],<BR>
[5, 2]<BR>
)

(%i92)

B2:mod(B,7);

(B2) matrix(<BR>
[6, 0],<BR>
[5, 2]<BR>
)

(%i93)

B2;

(%o93) matrix(<BR>
[6, 0],<BR>
[5, 2]<BR>
)

8 Definiranje funkcije

(%i94)

f(x):=x+sin(x);

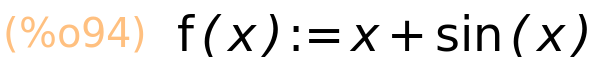
(%i95)

f(3);

(%i96)

f(3.0);

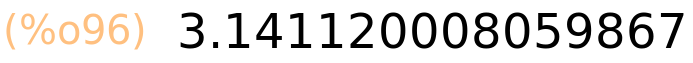
(%i97)

f(3),numer;

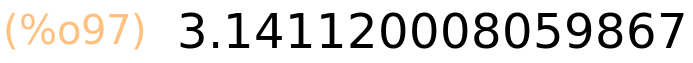
(%i98)

float(f(3));

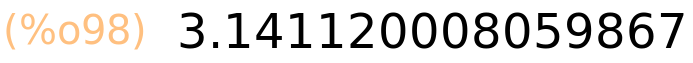
(%i99)

bfloat(f(3)),fpprec:50;

(%o99) 3.1411200080598672221007448028081102798469332642523b0

Možemo funkciju primijeniti i na elemente već ranije definirane matrice B

(%i100)

f(B);

(%o100) matrix(<BR>
[sin(34)+34, sin(21)+21],<BR>
[sin(12)+12, sin(58)+58]<BR>
)

(%i101)

f(B),numer;

(%o101) matrix(<BR>
[34.52908268612003, 21.83665563853605],<BR>
[11.46342708199957, 58.99287264808454]<BR>
)

možemo definirati "čistu" funkciju pomoću naredbe lambda

(%i102)

g:lambda([x],x+sin(x));

(%i103)

g(3);

(%i104)

g(3.0);

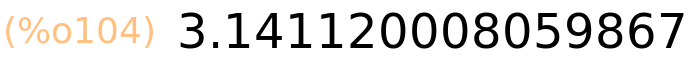
9 Tri osnovne naredbe za sređivanje izraza

(%i105)

izraz:(x+y)^5;

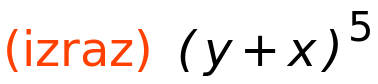
(%i106)

izraz;

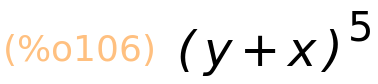
(%i107)

expand(izraz);

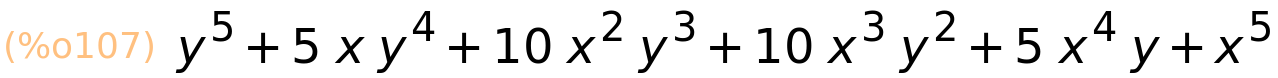
(%o107) y^5+5*x*y^4+10*x^2*y^3+10*x^3*y^2+5*x^4*y+x^5

(%i108)

izraz2:c^2+2·c·d+d^2;

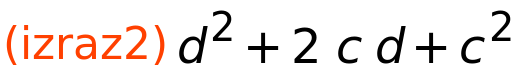
(%i109)

factor(izraz2);

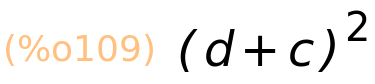
(%i110)

izraz3:(x+2)/(x+y)−2/(x^2+x·y);

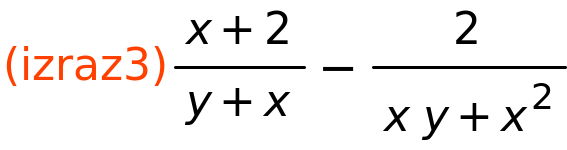
(%i111)

ratsimp(izraz3);

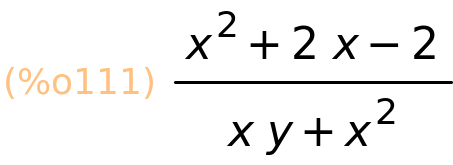
(%i112)

factor(izraz3);

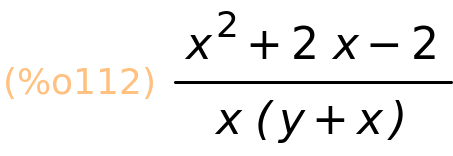
10 Rješavanje nekih jednadžbi i nejednadžbi

(%i113)

solve(x^2+3·x−4=0,x);

(%i114)

solve(x^2+3·x+5=0,x);

(%o114) [x=-(sqrt(11)*%i+3)/2,x=(sqrt(11)*%i-3)/2]

(%i115)

to_poly_solve(x^2+3·x−4>=0,x);

(%o115) %union([1<x],[x=-4],[x<-4],[x=1])

(%i116)

to_poly_solve(x^2+3·x−4>0,x);

možemo učitati paket fourier_elim i preko njega riješiti neke nejednadžbe

(%i117)

load(fourier_elim);

(%o117) "/usr/share/maxima/5.42.1/share/fourier_elim/fourier_elim.lisp"

(%i118)

fourier_elim(x^2+3·x−4>=0,[x]);

(%o118) [x=-4] or [x=1] or [1<x] or [x<-4]

(%i119)

fourier_elim((x+3)/(2·3−5)<=1,[x]);

(%i120)

to_poly_solve((x+3)/(2·3−5)<=1,x);

11 Dobivanje lijeve i desne strane zadane jednadžbe ili nejednadžbe

(%i121)

lhs(x^2+3·x=y+5·x^3);

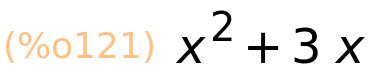
(%i122)

rhs(x^2+3·x=y+5·x^3);

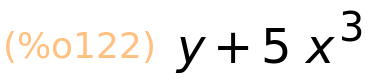
(%i123)

lhs(x+4>3+a);

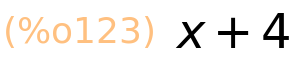
(%i124)

rhs(x+4>3+a);

12 Postavljanje pitanja maximi

Da li je 2 strogo manje od 5

(%i125)

is(2<5);

Da li je 3/4 veće ili jednako od 2

(%i126)

is(3/4>=2);

Da li je pi^e veće od e^pi

(%i127)

is(%pi^%e>%e^%pi);

(%i128)

%pi^%e,numer;

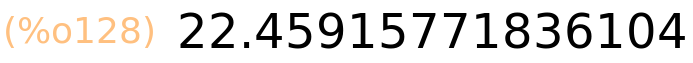
(%i129)

%e^%pi,numer;

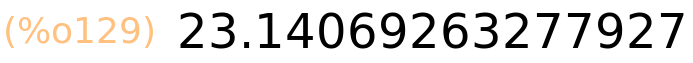
13 Kompleksni brojevi

imaginarna jedinica

(%i130)

%i;

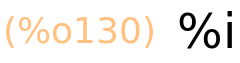
(%i131)

%i^2;

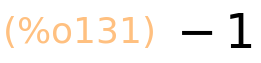
(%i133)

z1:3+2·%i;
z2:1/2−6/5·%i;

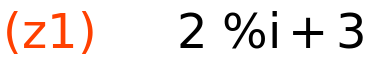
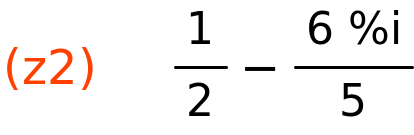
realni i imaginarni dio

(%i134)

realpart(z1);

(%i135)

imagpart(z1);

(%i136)

realpart(z2);

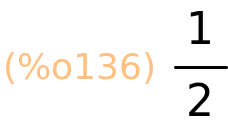
(%i137)

imagpart(z2);

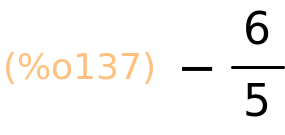
modul kompleksnog broja

(%i138)

abs(z1);

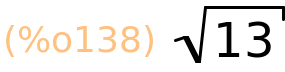
(%i139)

abs(z2);

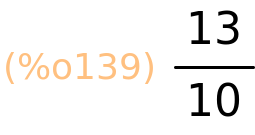
osnovne računske operacije s kompleksnim brojevima

(%i140)

z1+z2;

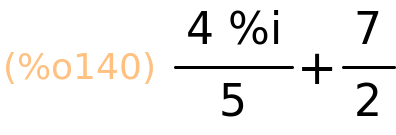
(%i141)

z1−z2;

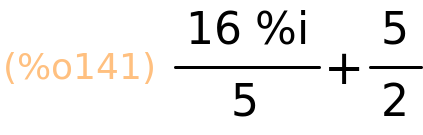
(%i142)

z1·z2;

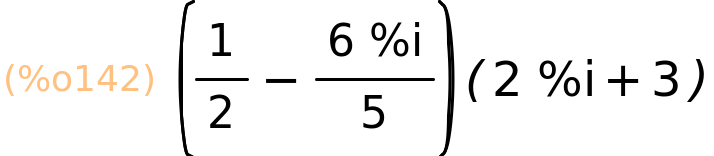
(%i143)

rectform(z1·z2);

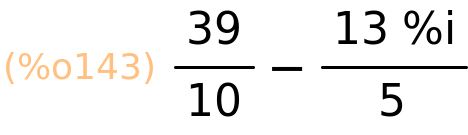
(%i144)

z1/z2;

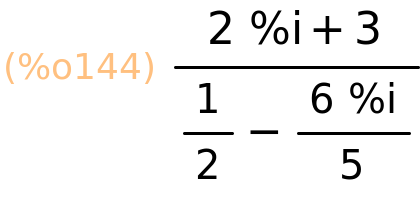
(%i145)

rectform(z1/z2);

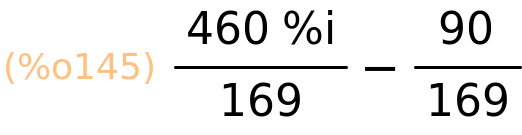
14 Supstitucija

(%i146)

izraz:x^2+2·x+y^3;

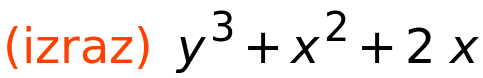
(%i147)

izraz;

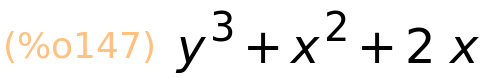
uvrsti u izraz x=2

(%i148)

subst(2,x,izraz);

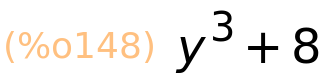
(%i149)

subst(x=2,izraz);

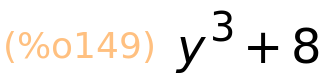
uvrsti u izraz x=2 i y=1/3

(%i150)

subst([x=2,y=1/3],izraz);

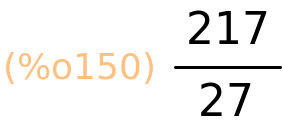
15 Liste

lista kvadrata prvih 10 prirodnih brojeva

(%i151)

lista:makelist(i^2,i,1,10);

treći element u listi

(%i152)

lista[3];

primijeni funkciju sinus na svaki element liste

(%i153)

map(sin,lista);

(%o153) [sin(1),sin(4),sin(9),sin(16),sin(25),sin(36),sin(49),sin(64),sin(81),sin(100)]

(%i154)

map(sin,lista),numer;

(%o154) [0.8414709848078965,-0.7568024953079282,0.4121184852417566,-0.2879033166650653,-0.132351750097773,-0.9917788534431158,-0.9537526527594719,0.9200260381967906,-0.6298879942744539,-0.5063656411097588]

primijeni funkciju f(x)=x^(1/3)+5 na svaki element liste

(%i155)

map(lambda([x],x^(1/3)+5),lista);

(%o155) [6,4^(1/3)+5,9^(1/3)+5,2^(4/3)+5,25^(1/3)+5,36^(1/3)+5,49^(1/3)+5,9,3^(4/3)+5,100^(1/3)+5]

(%i156)

map(lambda([x],x^(1/3)+5),lista),numer;

(%o156) [6.0,6.587401051968199,7.080083823051904,7.519842099789746,7.924017738212866,8.301927248894627,8.65930571002297,9.0,9.326748710922224,9.64158883361278]

uzmi iz promatrane liste samo parne brojeve

(%i157)

sublist(lista,evenp);

uzmi iz promatrane liste brojeve koji su između 15 i 80

(%i158)

sublist(lista,lambda([x],is(x>15 and x<80)));

16 Numeričko rješavanje polinomijalnih jednadžbi

solve ne zna rješavati polinomijalne jednadžbe stupnja strogo većeg od 4

(%i159)

solve(x^5−3·x^2−4·x+5=0,x);

Postoji naredba u maximi koja daje sva kompleksna rješenja polinomijalne jednadžbe

(%i160)

allroots(x^5−3·x^2−4·x+5=0);

(%o160) [x=0.8310908454342492,x=-1.37105778371704,x=1.632530667338985*%i-0.4861708139406671,x=-1.632530667338985*%i-0.4861708139406671,x=1.512308566164125]

ako želimo samo realna rješenja (jednostruka preciznost, približno na 6 decimala)

(%i161)

realroots(x^5−3·x^2−4·x+5=0);

(%o161) [x=-46005065/33554432,x=27886781/33554432,x=50744655/33554432]

(%i162)

realroots(x^5−3·x^2−4·x+5=0),numer;

(%o162) [x=-1.371057778596878,x=0.8310908377170563,x=1.512308567762375]

ako želimo samo realna rješenja (dvostruka preciznost, približno na 15 decimala)

(%i163)

realroots(x^5−3·x^2−4·x+5=0,1.0e−15);

(%o163) [x=-3087347661925739/2251799813685248,x=1871450210904357/2251799813685248,x=3405416147522981/2251799813685248]

(%i164)

realroots(x^5−3·x^2−4·x+5=0,1.0e−15),numer;

(%o164) [x=-1.37105778371704,x=0.8310908454342489,x=1.512308566164125]

Za rješavanje nepolinomijalnih jednadžbi moramo koristiti find_root naredbu.

To je detaljnije objašnjeno u drugom dokumentu.

(%i165)

allroots(sin(x)+cos(x)=0);

allroots: expected a polynomial; found sin(x)+cos(x)<BR>
-- an error. To debug this try: debugmode(true);

(%i166)

find_root(sin(x)+cos(x),1,5);

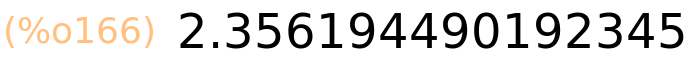
17 Polinomijalne jednadžne 3. i 4. stupnja

solve zna riješiti jednadžbu 3. stupnja

(%i167)

solve(x^3+3·x^2−x+2=0,x);

(%o167) [x=(4*((sqrt(3)*%i)/2+(-1)/2))/(3*(sqrt(419)/(2*3^(3/2))-5/2)^(1/3))+(sqrt(419)/(2*3^(3/2))-5/2)^(1/3)*((-1)/2-(sqrt(3)*%i)/2)-1,x=(sqrt(419)/(2*3^(3/2))-5/2)^(1/3)*((sqrt(3)*%i)/2+(-1)/2)+(4*((-1)/2-(sqrt(3)*%i)/2))/(3*(sqrt(419)/(2*3^(3/2))-5/2)^(1/3))-1,x=(sqrt(419)/(2*3^(3/2))-5/2)^(1/3)+4/(3*(sqrt(419)/(2*3^(3/2))-5/2)^(1/3))-1]

(%i168)

solve(x^3+3·x^2−x+2=0,x),numer;

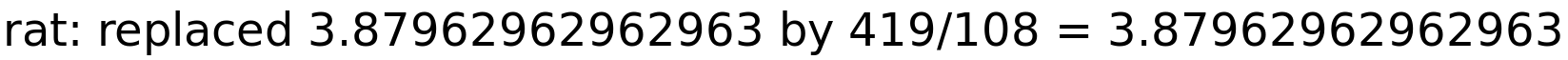
rat: replaced 3.87962962962963 by 419/108 = 3.87962962962963

(%o168) [x=-1.647247021725601*(0.8660254037844386*%i+(-1)/2)-0.8094313213185098*((-1)/2-0.8660254037844386*%i)-1,x=-0.8094313213185098*(0.8660254037844386*%i+(-1)/2)-1.647247021725601*((-1)/2-0.8660254037844386*%i)-1,x=-3.456678343044111]

pomoću allroots su elegantnije napisana rješenja

(%i169)

allroots(x^3+3·x^2−x+2=0);

(%o169) [x=0.725569680241994*%i+0.2283391715220555,x=0.2283391715220555-0.725569680241994*%i,x=-3.456678343044111]

solve zna riješiti jednadžbu 4. stupnja

(%i170)

solve(x^4+3·x^2−x−2=0,x);

(%o170) [x=-sqrt(-(2*sqrt(3)*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/6))/sqrt(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(2/3)-6*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)-5)-(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)+5/(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3))-4)/2-sqrt(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(2/3)-6*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)-5)/(2*sqrt(3)*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/6)),x=sqrt(-(2*sqrt(3)*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/6))/sqrt(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(2/3)-6*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)-5)-(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)+5/(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3))-4)/2-sqrt(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(2/3)-6*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)-5)/(2*sqrt(3)*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/6)),x=sqrt(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(2/3)-6*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)-5)/(2*sqrt(3)*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/6))-sqrt((2*sqrt(3)*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/6))/sqrt(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(2/3)-6*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)-5)-(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)+5/(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3))-4)/2,x=sqrt((2*sqrt(3)*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/6))/sqrt(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(2/3)-6*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)-5)-(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)+5/(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3))-4)/2+sqrt(3*(sqrt(10247)/(2*3^(3/2))+19/2)^(2/3)-6*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/3)-5)/(2*sqrt(3)*(sqrt(10247)/(2*3^(3/2))+19/2)^(1/6))]

(%i171)

solve(x^4+3·x^2−x−2=0,x),numer;

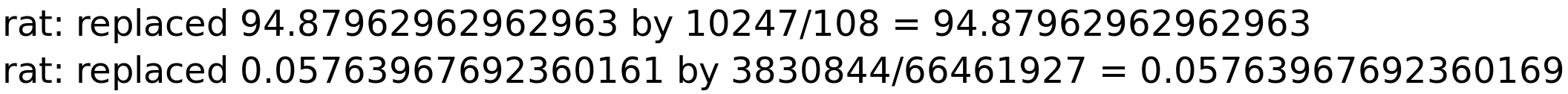
rat: replaced 94.87962962962963 by 10247/108 = 94.87962962962963<BR>
rat: replaced 0.05763967692360161 by 3830844/66461927 = 0.05763967692360169

(%o171) [x=-1.896582739058004*%i-0.1200413230137873,x=1.896582739058004*%i-0.1200413230137873,x=-0.6337532429197692,x=0.8738358889473439]

pomoću allroots su elegantnije napisana rješenja

(%i172)

allroots(x^4+3·x^2−x−2=0);

(%o172) [x=0.8738358889473413,x=-0.6337532429197662,x=1.896582739058003*%i-0.1200413230137876,x=-1.896582739058003*%i-0.1200413230137876]

18 Kako dobiti samo realna rješenja

Kada očekujemo samo realna rješenja jednadžbe, maxima nas ponekad može iznenaditi jer ona zna pronaći i kompleksna rješenja koja možda uopće ne očekujemo. Takav slučaj se može javiti kod eksponencijalne jednadžbe jer je eksponencijalna funkcija definirana za kompleksne brojeve. Ovdje nećemo ulaziti u detalje te definicije, nego nas samo zanima kako iz dobivenih rješenja uzeti samo ona koja su realna.

(%i173)

rj:solve(%e^(11/19·x)−5=0,x);

(rj) [x=19*log(5^(1/11)*%e^((2*%i*%pi)/11)),x=19*log(5^(1/11)*%e^((4*%i*%pi)/11)),x=19*log(5^(1/11)*%e^((6*%i*%pi)/11)),x=19*log(5^(1/11)*%e^((8*%i*%pi)/11)),x=19*log(5^(1/11)*%e^((10*%i*%pi)/11)),x=(19*log(5)-190*%i*%pi)/11,x=(19*log(5)-152*%i*%pi)/11,x=(19*log(5)-114*%i*%pi)/11,x=(19*log(5)-76*%i*%pi)/11,x=(19*log(5)-38*%i*%pi)/11,x=(19*log(5))/11]

Rješenja smo spremili u varijablu rj koja predstavlja listu.
Najprije pomoću naredbe map primijenimo funkciju rhs na svaki element liste kako bismo maknuli znakove jednakosti i ponovo spremimo u istu varijablu jer nam stara lista više ne treba (možemo spremiti i u neku novu varijablu, ali na ovaj način štedimo memoriju).

(%i174)

rj:map(rhs,rj);

(rj) [19*log(5^(1/11)*%e^((2*%i*%pi)/11)),19*log(5^(1/11)*%e^((4*%i*%pi)/11)),19*log(5^(1/11)*%e^((6*%i*%pi)/11)),19*log(5^(1/11)*%e^((8*%i*%pi)/11)),19*log(5^(1/11)*%e^((10*%i*%pi)/11)),(19*log(5)-190*%i*%pi)/11,(19*log(5)-152*%i*%pi)/11,(19*log(5)-114*%i*%pi)/11,(19*log(5)-76*%i*%pi)/11,(19*log(5)-38*%i*%pi)/11,(19*log(5))/11]

Sada pomoću sublist naredbe uzmemo samo one lemente iz liste čiji su imaginarni dijelovi jednaki nula (to su zapravo realna rješenja jednadžbe). U ovom slučaju imamo samo jedno realno rješenje.

(%i175)

rj:sublist(rj, lambda([x],imagpart(x)=0));

(%i176)

rj,numer;

Mogli smo sve napraviti u jednom koraku, ali namjerno je objašnjeno korak po korak da se lakše shvati ideja.

(%i177)

rj:solve(%e^(11/19·x)−5=0,x);

(%i178)

sublist(map(rhs,rj), lambda([x],imagpart(x)=0)),numer;

Created with wxMaxima.