1 Sustavi linearnih jednadžbi
1. zadatak
| (%i1) | linsolve([2*x+3*y+z=2, x-3*y+2*z=6, -2*x+6*y-z=3], [x,y,z]); |
![(%o1) [x=-7/3,y=5/9,z=5]](linearni_sustavi_htmlimg/linearni_sustavi_0.png)
matrica sustava
| (%i2) | M: coefmatrix([2*x+3*y+z=2, x-3*y+2*z=6, -2*x+6*y-z=3], [x,y,z]); |
![(M) matrix(<BR>
[2, 3, 1],<BR>
[1, -3, 2],<BR>
[-2, 6, -1]<BR>
)](linearni_sustavi_htmlimg/linearni_sustavi_1.png)
proširena matrica sustava (pazite: ovdje daje zadnji stupac slobodnih članova kako on izgleda s lijeve strane jednadžbe, a mi smo ga unosili onako kako izgleda s desne strane jednadžbe).
No, to je stvar dogovora i nema utjecaja na Kronecker-Capellijev teorem.
| (%i3) | Mp: augcoefmatrix([2*x+3*y+z=2, x-3*y+2*z=6, -2*x+6*y-z=3], [x,y,z]); |
![(Mp) matrix(<BR>
[2, 3, 1, -2],<BR>
[1, -3, 2, -6],<BR>
[-2, 6, -1, -3]<BR>
)](linearni_sustavi_htmlimg/linearni_sustavi_2.png)
Rang matrice sustava jednak je rangu proširene matrice sustava i taj rang je baš jednak broju varijabli.
Prema Kronecker-Capellijevom teoremu sustav ima jedinstveno rješenje.
| (%i4) | [rank(M),rank(Mp)]; |
![(%o4) [3,3]](linearni_sustavi_htmlimg/linearni_sustavi_3.png)
2. zadatak
| (%i5) | sustav: [x+y+2*z+3*u=6,x-4*y+2*z-3*u=-4,7*y+2*z+5*u=12,x+3*y+4*z+2*u=8]; |
![(sustav) [2*z+y+x+3*u=6,2*z-4*y+x-3*u=-4,2*z+7*y+5*u=12,4*z+3*y+x+2*u=8]](linearni_sustavi_htmlimg/linearni_sustavi_4.png)
varijabla u je parametar i pripadno bazično rješenje
| (%i6) | rj1:linsolve(sustav,[x,y,z,u]); |
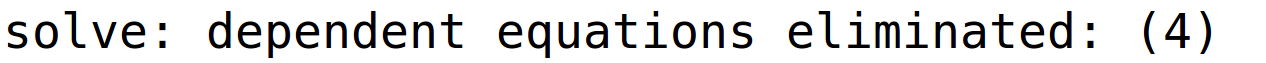
![(rj1) [x=-(26*%r1-30)/5,y=-(6*%r1-10)/5,z=(17*%r1-10)/10,u=%r1]](linearni_sustavi_htmlimg/linearni_sustavi_6.png)
| (%i7) | %rnum_list; |
![(%o7) [%r1]](linearni_sustavi_htmlimg/linearni_sustavi_7.png)
| (%i8) | subst(0,%rnum_list[1],rj1); |
![(%o8) [x=6,y=2,z=-1,u=0]](linearni_sustavi_htmlimg/linearni_sustavi_8.png)
varijabla z je parametar i pripadno bazično rješenje
| (%i9) | rj2: linsolve(sustav,[x,y,u,z]); |
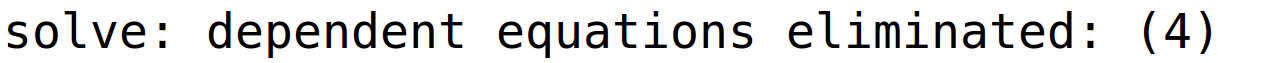
![(rj2) [x=-(52*%r2-50)/17,y=-(12*%r2-22)/17,u=(10+10*%r2)/17,z=%r2]](linearni_sustavi_htmlimg/linearni_sustavi_10.png)
| (%i10) | %rnum_list; |
![(%o10) [%r2]](linearni_sustavi_htmlimg/linearni_sustavi_11.png)
| (%i11) | subst(0,%rnum_list[1],rj2); |
![(%o11) [x=50/17,y=22/17,u=10/17,z=0]](linearni_sustavi_htmlimg/linearni_sustavi_12.png)
varijabla y je parametar i pripadno bazično rješenje
| (%i12) | rj3:linsolve(sustav,[x,z,u,y]); |
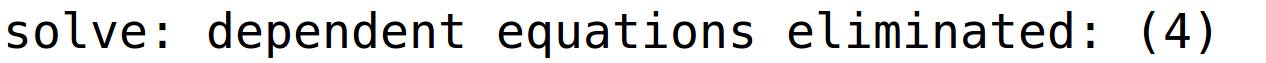
![(rj3) [x=(13*%r3-8)/3,z=-(17*%r3-22)/12,u=-(5*%r3-10)/6,y=%r3]](linearni_sustavi_htmlimg/linearni_sustavi_14.png)
| (%i13) | %rnum_list; |
![(%o13) [%r3]](linearni_sustavi_htmlimg/linearni_sustavi_15.png)
| (%i14) | subst(0,%rnum_list[1],rj3); |
![(%o14) [x=-8/3,z=11/6,u=5/3,y=0]](linearni_sustavi_htmlimg/linearni_sustavi_16.png)
varijabla x je parametar i pripadno bazično rješenje
| (%i15) | rj4:linsolve(sustav,[y,z,u,x]); |
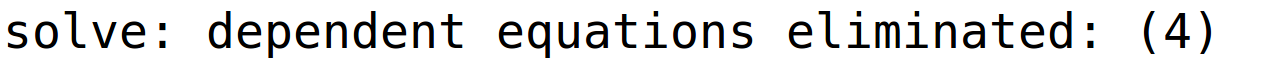
![(rj4) [y=(8+3*%r4)/13,z=-(17*%r4-50)/52,u=-(5*%r4-30)/26,x=%r4]](linearni_sustavi_htmlimg/linearni_sustavi_18.png)
| (%i16) | %rnum_list; |
![(%o16) [%r4]](linearni_sustavi_htmlimg/linearni_sustavi_19.png)
| (%i17) | subst(0,%rnum_list[1],rj4); |
![(%o17) [y=8/13,z=25/26,u=15/13,x=0]](linearni_sustavi_htmlimg/linearni_sustavi_20.png)
ako ne želimo uvoditi nova slova za parametre
| (%i18) | linsolve_params: false$ |
varijabla u je parametar
| (%i19) | r1:linsolve(sustav,[x,y,z,u]); |
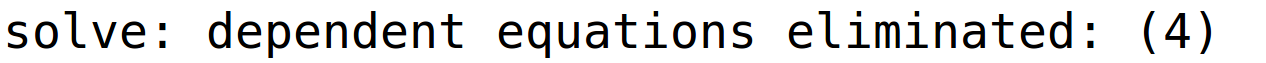
![(r1) [x=-(26*u-30)/5,y=-(6*u-10)/5,z=(17*u-10)/10]](linearni_sustavi_htmlimg/linearni_sustavi_22.png)
pripadno bazično rješenje (sada nigdje ne piše u=0 jer je slovo u ujedno i parametar, ali znamo da smo uvrstili u=0 u opće rješenje)
| (%i20) | subst(0,u,r1); |
![(%o20) [x=6,y=2,z=-1]](linearni_sustavi_htmlimg/linearni_sustavi_23.png)
varijabla z je parametar
| (%i21) | r2:linsolve(sustav,[x,y,u,z]); |
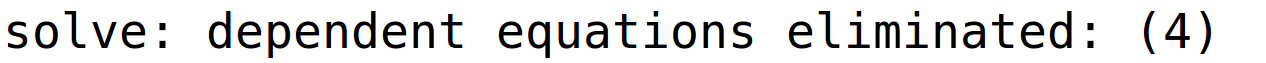
![(r2) [x=-(52*z-50)/17,y=-(12*z-22)/17,u=(10+10*z)/17]](linearni_sustavi_htmlimg/linearni_sustavi_25.png)
pripadno bazično rješenje (sada nigdje ne piše z=0 jer je slovo u ujedno i parametar, ali znamo da smo uvrstili z=0 u opće rješenje)
| (%i22) | subst(0,z,r2); |
![(%o22) [x=50/17,y=22/17,u=10/17]](linearni_sustavi_htmlimg/linearni_sustavi_26.png)
varijabla y je parametar
| (%i23) | r3:linsolve(sustav,[x,z,u,y]); |
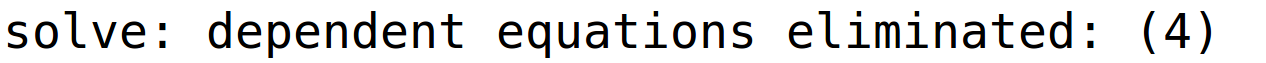
![(r3) [x=(13*y-8)/3,z=-(17*y-22)/12,u=-(5*y-10)/6]](linearni_sustavi_htmlimg/linearni_sustavi_28.png)
pripadno bazično rješenje (sada nigdje ne piše y=0 jer je slovo u ujedno i parametar, ali znamo da smo uvrstili y=0 u opće rješenje)
| (%i24) | subst(0,y,r3); |
![(%o24) [x=-8/3,z=11/6,u=5/3]](linearni_sustavi_htmlimg/linearni_sustavi_29.png)
varijabla x je parametar
| (%i25) | r4:linsolve(sustav,[y,z,u,x]); |
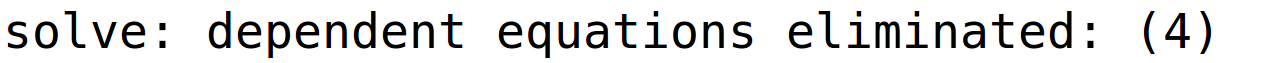
![(r4) [y=(8+3*x)/13,z=-(17*x-50)/52,u=-(5*x-30)/26]](linearni_sustavi_htmlimg/linearni_sustavi_31.png)
pripadno bazično rješenje (sada nigdje ne piše x=0 jer je slovo u ujedno i parametar, ali znamo da smo uvrstili x=0 u opće rješenje)
| (%i26) | subst(0,x,r4); |
![(%o26) [y=8/13,z=25/26,u=15/13]](linearni_sustavi_htmlimg/linearni_sustavi_32.png)
matrica sustava
| (%i27) | M: coefmatrix(sustav,[x,y,z,u]); |
![(M) matrix(<BR>
[1, 1, 2, 3],<BR>
[1, -4, 2, -3],<BR>
[0, 7, 2, 5],<BR>
[1, 3, 4, 2]<BR>
)](linearni_sustavi_htmlimg/linearni_sustavi_33.png)
proširena matrica sustava
| (%i28) | Mp: augcoefmatrix(sustav,[x,y,z,u]); |
![(Mp) matrix(<BR>
[1, 1, 2, 3, -6],<BR>
[1, -4, 2, -3, 4],<BR>
[0, 7, 2, 5, -12],<BR>
[1, 3, 4, 2, -8]<BR>
)](linearni_sustavi_htmlimg/linearni_sustavi_34.png)
Rang matrice sustava jednak je rangu proširene matrice sustava i taj rang je manji od broja varijabli.
Prema Kronecker-Capellijevom teoremu sustav ima beskonačno mnogo rješenja.
| (%i29) | [rank(M),rank(Mp)]; |
![(%o29) [3,3]](linearni_sustavi_htmlimg/linearni_sustavi_35.png)
uvjet pod kojim je suma komponenata rješenja pozitivna ako uzmemo opće rješenje u kojemu je varijabla y parametar
| (%i30) | r3; |
![(%o30) [x=(13*y-8)/3,z=-(17*y-22)/12,u=-(5*y-10)/6]](linearni_sustavi_htmlimg/linearni_sustavi_36.png)
suma komponenata rješenja (dva načina - ručno ispisivanje ili korištenje naredbe sum)
naredba rhs nam daje desnu stranu u jednakosti, a naredba lhs daje lijevu stranu u jednakosti
| (%i31) | [r3[1],lhs(r3[1]),rhs(r3[1])]; |
![(%o31) [x=(13*y-8)/3,x,(13*y-8)/3]](linearni_sustavi_htmlimg/linearni_sustavi_37.png)
| (%i32) | rhs(r3[1])+rhs(r3[2])+rhs(r3[3])+y; |
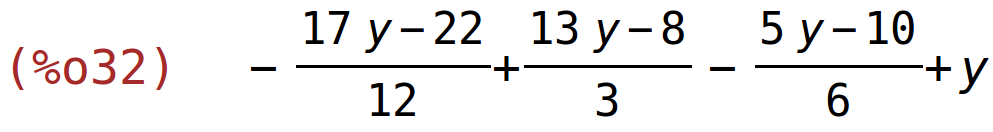
| (%i33) | nejednakost:sum(rhs(r3[i]),i,1,3)+y; |
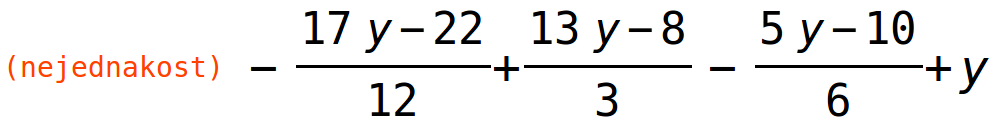
rješavanje nejednadžbe - dva načina:
1. način: pomoću naredbe to_poly_solve
2. način: pomoću naredbe fourier_elim koju najprije treba učitati pomoću naredbe load
| (%i34) | to_poly_solve(nejednakost>0,y); |
![(%o34) %union([-10/37<y])](linearni_sustavi_htmlimg/linearni_sustavi_41.png)
| (%i35) | load(fourier_elim)$ |
| (%i36) | fourier_elim([nejednakost>0],[y]); |
![(%o36) [-10/37<y]](linearni_sustavi_htmlimg/linearni_sustavi_42.png)
3. zadatak
| (%i37) | sustav2: [2*x1+3*x2+2*x3+6*x4=1,-2*x1+3*x2-6*x3+12*x4=-19,2*x1+6*x2+15*x4=-8]; |
![(sustav2) [6*x4+2*x3+3*x2+2*x1=1,12*x4-6*x3+3*x2-2*x1=-19,15*x4+6*x2+2*x1=-8]](linearni_sustavi_htmlimg/linearni_sustavi_43.png)
pazite: već ranije smo bili stavili linsolve_params: false$ pa se neće uvoditi nova slova za parametre osim ako ponovo ne stavimo vrijednost spomenute varijable na true
varijable x3 i x4 su parametri i pripadno bazično rješenje
| (%i38) | r34:linsolve(sustav2,[x1,x2,x3,x4]); |
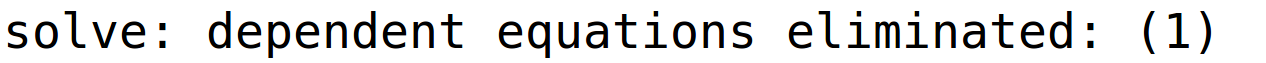
![(r34) [x1=(10-4*x3+3*x4)/2,x2=-(9-2*x3+9*x4)/3]](linearni_sustavi_htmlimg/linearni_sustavi_45.png)
| (%i39) | subst([x3=0,x4=0],r34); |
![(%o39) [x1=5,x2=-3]](linearni_sustavi_htmlimg/linearni_sustavi_46.png)
varijable x1 i x2 su parametri i pripadno bazično rješenje
| (%i40) | r12:linsolve(sustav2,[x3,x4,x1,x2]); |
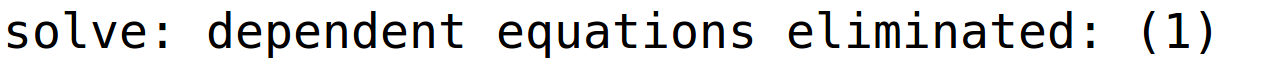
![(r12) [x3=-(-21+6*x1+3*x2)/10,x4=-(8+2*x1+6*x2)/15]](linearni_sustavi_htmlimg/linearni_sustavi_48.png)
| (%i41) | subst([x1=0,x2=0],r12); |
![(%o41) [x3=21/10,x4=-8/15]](linearni_sustavi_htmlimg/linearni_sustavi_49.png)
varijable x1 i x3 su parametri i pripadno bazično rješenje
| (%i42) | r13:linsolve(sustav2,[x2,x4,x1,x3]); |
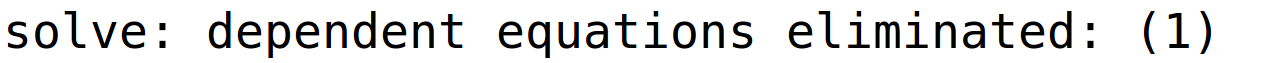
![(r13) [x2=-(-21+6*x1+10*x3)/3,x4=(-10+2*x1+4*x3)/3]](linearni_sustavi_htmlimg/linearni_sustavi_51.png)
| (%i43) | subst([x1=0,x3=0],r13); |
![(%o43) [x2=7,x4=-10/3]](linearni_sustavi_htmlimg/linearni_sustavi_52.png)
varijable x1 i x4 su parametri i pripadno bazično rješenje
| (%i44) | r14:linsolve(sustav2,[x2,x3,x1,x4]); |
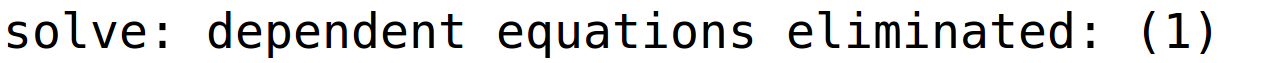
![(r14) [x2=-(8+2*x1+15*x4)/6,x3=(10-2*x1+3*x4)/4]](linearni_sustavi_htmlimg/linearni_sustavi_54.png)
| (%i45) | subst([x1=0,x4=0],r14); |
![(%o45) [x2=-4/3,x3=5/2]](linearni_sustavi_htmlimg/linearni_sustavi_55.png)
varijable x2 i x3 su parametri i pripadno bazično rješenje
| (%i46) | r23:linsolve(sustav2,[x1,x4,x2,x3]); |
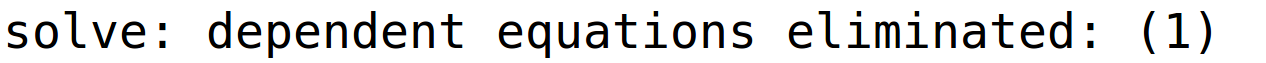
![(r23) [x1=-(-21+3*x2+10*x3)/6,x4=(-9-3*x2+2*x3)/9]](linearni_sustavi_htmlimg/linearni_sustavi_57.png)
| (%i47) | subst([x2=0,x3=0],r23); |
![(%o47) [x1=7/2,x4=-1]](linearni_sustavi_htmlimg/linearni_sustavi_58.png)
varijable x2 i x4 su parametri i pripadno bazično rješenje
| (%i48) | r24:linsolve(sustav2,[x1,x3,x2,x4]); |
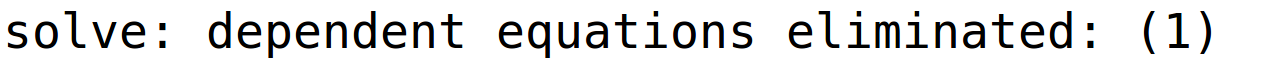
![(r24) [x1=-(8+6*x2+15*x4)/2,x3=(9+3*x2+9*x4)/2]](linearni_sustavi_htmlimg/linearni_sustavi_60.png)
| (%i49) | subst([x2=0,x4=0],r24); |
![(%o49) [x1=-4,x3=9/2]](linearni_sustavi_htmlimg/linearni_sustavi_61.png)
matrica sustava
| (%i50) | M:coefmatrix(sustav2,[x1,x2,x3,x4]); |
![(M) matrix(<BR>
[2, 3, 2, 6],<BR>
[-2, 3, -6, 12],<BR>
[2, 6, 0, 15]<BR>
)](linearni_sustavi_htmlimg/linearni_sustavi_62.png)
proširena matrica sustava
| (%i51) | Mp:augcoefmatrix(sustav2,[x1,x2,x3,x4]); |
![(Mp) matrix(<BR>
[2, 3, 2, 6, -1],<BR>
[-2, 3, -6, 12, 19],<BR>
[2, 6, 0, 15, 8]<BR>
)](linearni_sustavi_htmlimg/linearni_sustavi_63.png)
Rang matrice sustava jednak je rangu proširene matrice sustava i taj rang je manji od broja varijabli.
Prema Kronecker-Capellijevom teoremu sustav ima beskonačno mnogo rješenja.
| (%i52) | [rank(M),rank(Mp)]; |
![(%o52) [2,2]](linearni_sustavi_htmlimg/linearni_sustavi_64.png)
4. zadatak - kontradiktorni sustav
| (%i53) | sustav3:[x1-4*x2+5*x3=6,-3*x2+2*x3=-12,2*x1+7*x2=35]$ |
| (%i54) | linsolve(sustav3,[x1,x2,x3]); |
![(%o54) []](linearni_sustavi_htmlimg/linearni_sustavi_65.png)
matrica sustava
| (%i55) | M:coefmatrix(sustav3,[x1,x2,x3]); |
![(M) matrix(<BR>
[1, -4, 5],<BR>
[0, -3, 2],<BR>
[2, 7, 0]<BR>
)](linearni_sustavi_htmlimg/linearni_sustavi_66.png)
proširena matrica sustava
| (%i56) | Mp:augcoefmatrix(sustav3,[x1,x2,x3]); |
![(Mp) matrix(<BR>
[1, -4, 5, -6],<BR>
[0, -3, 2, 12],<BR>
[2, 7, 0, -35]<BR>
)](linearni_sustavi_htmlimg/linearni_sustavi_67.png)
Rang matrice sustava je različit od ranga proširene matrice sustava.
Prema Kronecker-Capellijevom teoremu sustav je kontradiktoran.
| (%i57) | [rank(M),rank(Mp)]; |
![(%o57) [2,3]](linearni_sustavi_htmlimg/linearni_sustavi_68.png)
5. zadatak
| (%i58) | sustav4:[-4*x1-3*x2-4*x3=-1,x1+x2+x3=1,14*x1+11*x2+14*x3=5,11*x1+9*x2+11*x3=5]$ |
varijabla x3 je parametar i pripadno bazično rješenje
| (%i59) | r1:linsolve(sustav4,[x1,x2,x3]); |
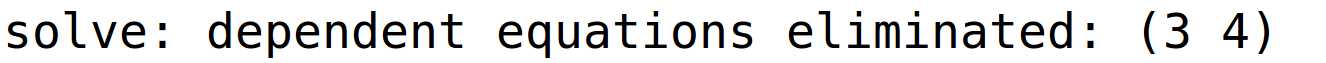
![(r1) [x1=-x3-2,x2=3]](linearni_sustavi_htmlimg/linearni_sustavi_70.png)
| (%i60) | subst([x3=0],r1); |
![(%o60) [x1=-2,x2=3]](linearni_sustavi_htmlimg/linearni_sustavi_71.png)
varijabla x1 je parametar i pripadno bazično rješenje
| (%i61) | r2:linsolve(sustav4,[x3,x2,x1]); |
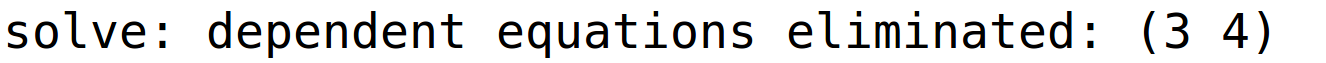
![(r2) [x3=-x1-2,x2=3]](linearni_sustavi_htmlimg/linearni_sustavi_73.png)
| (%i62) | subst([x1=0],r2); |
![(%o62) [x3=-2,x2=3]](linearni_sustavi_htmlimg/linearni_sustavi_74.png)
matrica sustava
| (%i63) | M:coefmatrix(sustav4,[x1,x2,x3]); |
![(M) matrix(<BR>
[-4, -3, -4],<BR>
[1, 1, 1],<BR>
[14, 11, 14],<BR>
[11, 9, 11]<BR>
)](linearni_sustavi_htmlimg/linearni_sustavi_75.png)
proširena matrica sustava
| (%i64) | Mp:augcoefmatrix(sustav4,[x1,x2,x3]); |
![(Mp) matrix(<BR>
[-4, -3, -4, 1],<BR>
[1, 1, 1, -1],<BR>
[14, 11, 14, -5],<BR>
[11, 9, 11, -5]<BR>
)](linearni_sustavi_htmlimg/linearni_sustavi_76.png)
Rang matrice sustava jednak je rangu proširene matrice sustava i taj rang je manji od broja varijabli.
Prema Kronecker-Capellijevom teoremu sustav ima beskonačno mnogo rješenja.
| (%i65) | [rank(M),rank(Mp)]; |
![(%o65) [2,2]](linearni_sustavi_htmlimg/linearni_sustavi_77.png)
2 Nejednadžbe
rješavanje nejednadžbe - dva načina:
1. način: pomoću naredbe to_poly_solve
2. način: pomoću naredbe fourier_elim koju najprije treba učitati pomoću naredbe load
| (%i66) | load(fourier_elim)$ |
1. zadatak
| (%i67) | to_poly_solve(2*x-3/5>(5*x-3)/2,x); |
![(%o67) %union([x<9/5])](linearni_sustavi_htmlimg/linearni_sustavi_78.png)
| (%i68) | fourier_elim([2*x-3/5>(5*x-3)/2],[x]); |
![(%o68) [x<9/5]](linearni_sustavi_htmlimg/linearni_sustavi_79.png)
2. zadatak
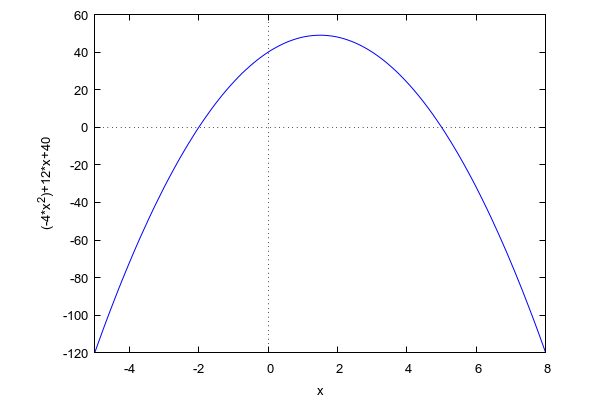
| (%i69) | to_poly_solve(-4*x^2+12*x+40<=0,x); |
![(%o69) %union([5<x],[x=-2],[x<-2],[x=5])](linearni_sustavi_htmlimg/linearni_sustavi_80.png)
| (%i70) | fourier_elim([-4*x^2+12*x+40<=0],[x]); |
![(%o70) [x=-2] or [x=5] or [5<x] or [x<-2]](linearni_sustavi_htmlimg/linearni_sustavi_81.png)
| (%i71) | wxplot2d([-4*x^2+12*x+40], [x,-5,8],[axes,true])$ |

| (%i72) |
plot2d([-4*x^2+12*x+40], [x,-5,8], [gnuplot_preamble, "set grid;"])$ |
| (%i73) | to_poly_solve(-4*x^2+12*x+40>0,x); |
![(%o73) %union([-2<x,x<5])](linearni_sustavi_htmlimg/linearni_sustavi_84.png)
| (%i74) | fourier_elim([-4*x^2+12*x+40>0],[x]); |
![(%o74) [-2<x,x<5]](linearni_sustavi_htmlimg/linearni_sustavi_85.png)
3. zadatak
| (%i75) | load("draw")$ |
| (%i76) | to_poly_solve([3*x1-4*x2<=6,3*x1+4*x2<=12,2*x1-x2>=0],[x1,x2]); |
![(%o76) %union([x1=-6/5,x2=-12/5],[x1=12/11,x2=24/11],[x1=3,x2=3/4],[x1=x2/2,-12/5<x2,x2<24/11],[x1=-(4*x2-12)/3,3/4<x2,x2<24/11],[x1=(6+4*x2)/3,-12/5<x2,x2<3/4],[x2/2<x1,x1<min((4*x2)/3+2,4-(4*x2)/3),-12/5<x2,x2<24/11])](linearni_sustavi_htmlimg/linearni_sustavi_86.png)
| (%i77) | fourier_elim([3*x1-4*x2<=6,3*x1+4*x2<=12,2*x1-x2>=0],[x1,x2]); |
![(%o77) [x1=12/11,x2=24/11] or [x1=-6/5,x2=-12/5] or [x1=x2/2,-12/5<x2,x2<24/11] or [x1=3,x2=3/4] or [x1=-(4*x2-12)/3,3/4<x2,x2<24/11] or [x1=(6+4*x2)/3,-12/5<x2,x2<3/4] or [x2/2<x1,x1<min((4*x2)/3+2,4-(4*x2)/3),-12/5<x2,x2<24/11]](linearni_sustavi_htmlimg/linearni_sustavi_87.png)
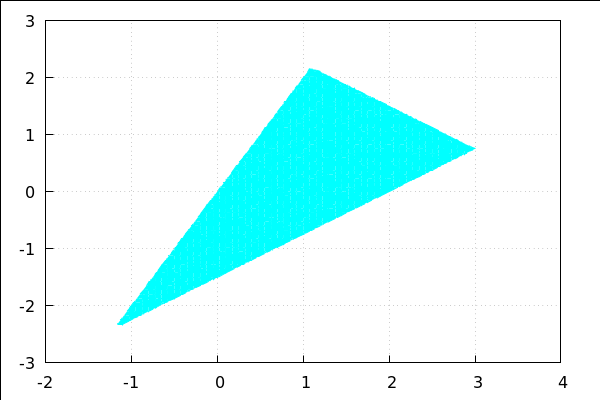
| (%i78) |
wxdraw2d(grid=true, x_voxel=80, y_voxel=80,fill_color = cyan, region(3*x-4*y<=6 and 3*x+4*y<=12 and 2*x-y>=0, x,-2,4, y,-3,3)); |


4. zadatak
| (%i79) | to_poly_solve([-12*x1+3*x2<=3,4*x1-10*x2<=5,x1>=0],[x1,x2]); |
![(%o79) %union([max(0,x2/4-1/4)<x1,x1<(5*x2)/2+5/4,-1/2<x2],[x1=0,-1/2<x2,x2<1],[x1=0,x2=-1/2],[x1=0,x2=1],[x1=(x2-1)/4,1<x2],[x1=(5+10*x2)/4,-1/2<x2])](linearni_sustavi_htmlimg/linearni_sustavi_91.png)
| (%i80) | fourier_elim([-12*x1+3*x2<=3,4*x1-10*x2<=5,x1>=0],[x1,x2]); |
![(%o80) [x1=0,x2=-1/2] or [x1=0,x2=1] or [x1=0,-1/2<x2,x2<1] or [x1=(5+10*x2)/4,-1/2<x2] or [x1=(x2-1)/4,1<x2] or [max(0,x2/4-1/4)<x1,x1<(5*x2)/2+5/4,-1/2<x2]](linearni_sustavi_htmlimg/linearni_sustavi_92.png)
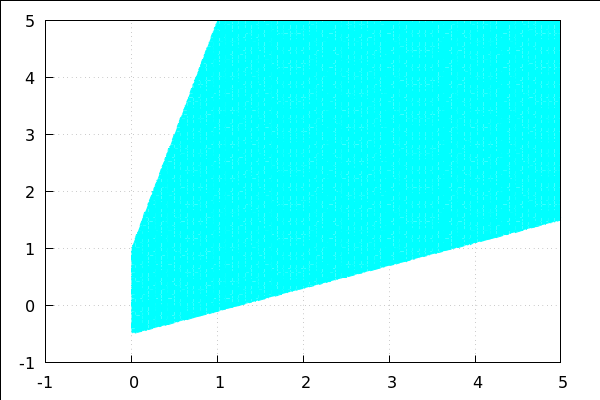
| (%i81) |
wxdraw2d(grid=true, x_voxel=80, y_voxel=80,fill_color = cyan, region(-12*x+3*y<=3 and 4*x-10*y<=5 and x>=0, x,-1,5, y,-1,5)); |

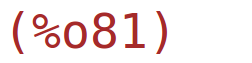
5. zadatak
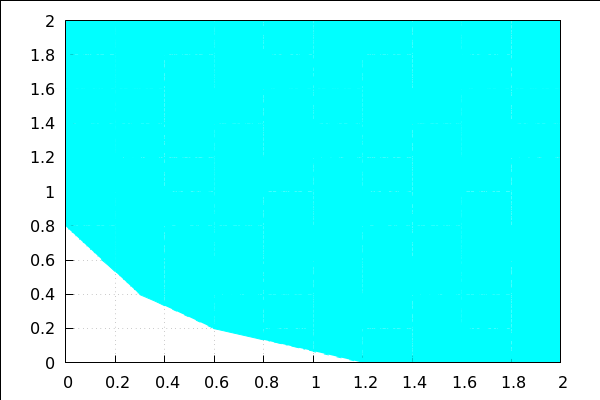
| (%i82) | to_poly_solve([3*x+2*y>2,3*x+2*y<=6],[x,y]); |
![(%o82) %union([x=-(2*y-6)/3],[2/3-(2*y)/3<x,x<2-(2*y)/3])](linearni_sustavi_htmlimg/linearni_sustavi_96.png)
| (%i83) | fourier_elim([3*x+2*y>2,3*x+2*y<=6],[x,y]); |
![(%o83) [x=-(2*y-6)/3] or [2/3-(2*y)/3<x,x<2-(2*y)/3]](linearni_sustavi_htmlimg/linearni_sustavi_97.png)
| (%i84) | wxdraw2d(grid=true, fill_color = cyan, region(3*x+2*y>2 and 3*x+2*y<=6, x,-3,3, y,-5,5))$ |

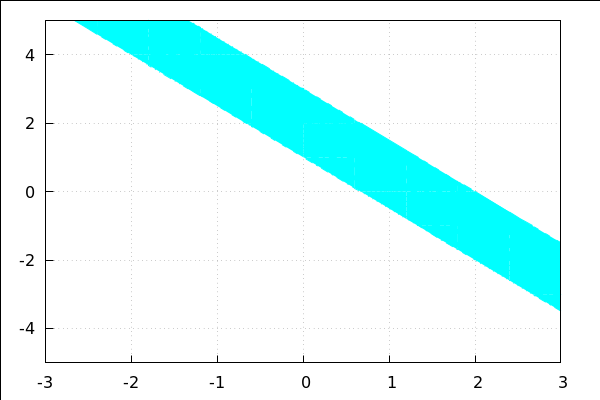
3 Linearno programiranje
| (%i85) | load(simplex)$ |
1. zadatak: Draguljar - prstenje i privjeski
| (%i86) | maximize_lp(8*x+10*y,[4*x+2*y<=40, 0.2*x+0.4*y<=5.6]), nonegative_lp=true; |
![(%o86) [152.0,[y=11.99999999999999,x=4.000000000000001]]](linearni_sustavi_htmlimg/linearni_sustavi_100.png)
| (%i87) | wxdraw2d(grid=true,fill_color=cyan, region(4*x+2*y<=40 and 0.2*x+0.4*y<=5.6, x,0,11, y,0,15)); |

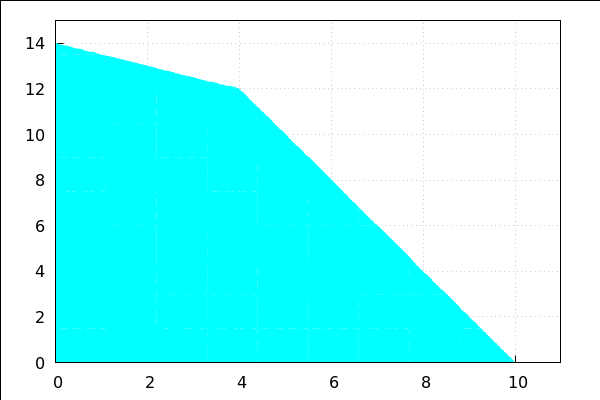

2. zadatak - generator i dvije vrste goriva
| (%i88) | minimize_lp(3*x+2.5*y, [x+y>=4, 3*x+5*y<=15]), nonegative_lp=true; |
![(%o88) [11.25,[y=3/2,x=5/2]]](linearni_sustavi_htmlimg/linearni_sustavi_104.png)
| (%i89) |
wxdraw2d(grid=true,x_voxel=100, y_voxel=100, xtics=[0,0.5,6], fill_color=cyan, region(x+y>=4 and 3*x+5*y<=15, x,0,6, y,0,2)); |

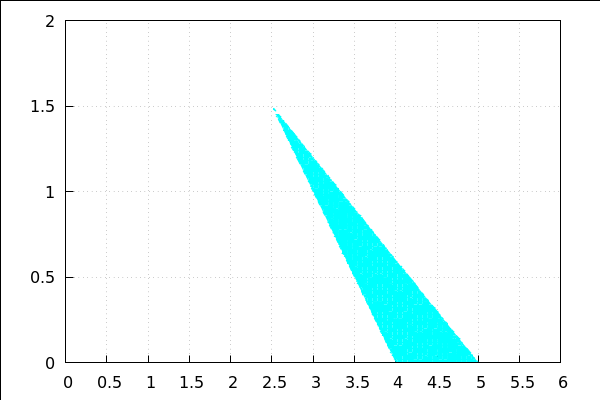

3. zadatak - prehrana životinja s dvije vrste stočne hrane
| (%i90) | minimize_lp(2.5*x+3*y, [20*x+30*y>=18, 10*x+30*y>=12, 80*x+60*y>=48]), nonegative_lp=true; |
![(%o90) [1.95,[y=2/5,x=3/10]]](linearni_sustavi_htmlimg/linearni_sustavi_108.png)
maksimum ne postoji
| (%i91) | maximize_lp(2.5*x+3*y, [20*x+30*y>=18, 10*x+30*y>=12, 80*x+60*y>=48]), nonegative_lp=true; |
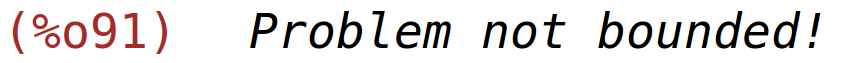
| (%i92) |
wxdraw2d(grid=true,fill_color=cyan, xtics=[0,0.2,2], ytics=[0,0.2,2], region(20*x+30*y>=18 and 10*x+30*y>=12 and 80*x+60*y>=48, x, 0, 2, y, 0, 2)); |