Bojanje vrhova i bridova grafa u pythonu. Sparivanje u grafu

In [1]:
import platform
In [2]:
platform.platform()
Out[2]:
'Linux-4.19.4-1-MANJARO-x86_64-with-arch-Manjaro-Linux'
In [3]:
platform.python_version()
Out[3]:
'3.7.1'
In [4]:
import warnings
warnings.filterwarnings("ignore")
In [5]:
import networkx as nx
In [6]:
nx.__version__
Out[6]:
'2.2'
In [7]:
from pylab import *
In [8]:
%matplotlib inline
In [9]:
import matplotlib as plt
In [10]:
plt.__version__
Out[10]:
'3.0.2'
In [11]:
import DSTG

Planarni grafovi

$K_{2,3}$ je planarni graf

In [12]:
K23=nx.complete_bipartite_graph(2,3)
nx.check_planarity(K23)
Out[12]:
(True, <networkx.algorithms.planarity.PlanarEmbedding at 0x7ff269493518>)

Lista susjedstva tako da su svi vrhovi sortirani u smjeru obilaska kazaljke na satu

In [13]:
nx.check_planarity(K23)[1].get_data()
Out[13]:
{0: [2, 4, 3], 1: [2, 3, 4], 2: [0, 1], 3: [1, 0], 4: [1, 0]}

Neko ravninsko smještenje od $K_{2,3}$

In [14]:
nx.draw(K23,with_labels=True,pos={0:[0,2],1:[0,0],2:[-1,1],3:[1,1],4:[0,1]},node_color='y')

$K_{3,3}$ nije planarni graf

In [15]:
K33=nx.complete_bipartite_graph(3,3)
nx.check_planarity(K33)
Out[15]:
(False, None)

$K_5$ nije planarni graf

In [16]:
K5=nx.complete_graph(5)
nx.check_planarity(K5)
Out[16]:
(False, None)

Petersenov graf nije planarni graf

In [17]:
P=nx.petersen_graph()
nx.check_planarity(P)
Out[17]:
(False, None)

$K_4$ je planarni graf

In [18]:
K4=nx.complete_graph(4)
nx.check_planarity(K4)
Out[18]:
(True, <networkx.algorithms.planarity.PlanarEmbedding at 0x7ff267446780>)

Neko ravninsko smještenje od $K_4$

In [19]:
nx.draw(K4,with_labels=True,pos={0:[0,0],1:[1,1],2:[2,0],3:[1,0.4]},node_color='y')

Platonova tijela

Platonova tijela su planarni grafovi.

Kocka

In [20]:
kocka=nx.cubical_graph()
nx.check_planarity(kocka)
Out[20]:
(True, <networkx.algorithms.planarity.PlanarEmbedding at 0x7ff267411be0>)

Neko ravninsko smještenje

$\nu=8,\ \varepsilon=12,\ \Phi=6,\ \nu-\varepsilon+\Phi=2$

In [21]:
figure(figsize=(4,4))
nx.draw(kocka,pos=DSTG.PLATON['KOCKA'],with_labels=True,node_color='y')

Tetraedar

In [22]:
tetraedar=nx.tetrahedral_graph()
nx.check_planarity(tetraedar)
Out[22]:
(True, <networkx.algorithms.planarity.PlanarEmbedding at 0x7ff267391d30>)

Neko ravninsko smještenje

$\nu=4,\ \varepsilon=6,\ \Phi=4,\ \nu-\varepsilon+\Phi=2$

In [23]:
figure(figsize=(4,4))
nx.draw(tetraedar,pos=DSTG.PLATON['TETRAEDAR'],with_labels=True,node_color='y')

Oktaedar

In [24]:
oktaedar=nx.octahedral_graph()
nx.check_planarity(oktaedar)
Out[24]:
(True, <networkx.algorithms.planarity.PlanarEmbedding at 0x7ff2672f76d8>)

Neko ravninsko smještenje

$\nu=6,\ \varepsilon=12,\ \Phi=8,\ \nu-\varepsilon+\Phi=2$

In [25]:
figure(figsize=(4,4))
nx.draw(oktaedar,pos=DSTG.PLATON['OKTAEDAR'],with_labels=True,node_color='y')

Dodekaedar

In [26]:
dodekaedar=nx.dodecahedral_graph()
nx.check_planarity(dodekaedar)
Out[26]:
(True, <networkx.algorithms.planarity.PlanarEmbedding at 0x7ff2672cf400>)

Neko ravninsko smještenje

$\nu=20,\ \varepsilon=30,\ \Phi=12,\ \nu-\varepsilon+\Phi=2$

In [27]:
figure(figsize=(5,5))
nx.draw(dodekaedar,pos=DSTG.PLATON['DODEKAEDAR'],with_labels=True,node_color='y')

Ikozaedar

In [28]:
ikozaedar=nx.icosahedral_graph()
nx.check_planarity(ikozaedar)
Out[28]:
(True, <networkx.algorithms.planarity.PlanarEmbedding at 0x7ff267233da0>)

Neko ravninsko smještenje

$\nu=12,\ \varepsilon=30,\ \Phi=20,\ \nu-\varepsilon+\Phi=2$

In [29]:
figure(figsize=(6,6))
nx.draw(ikozaedar,pos=DSTG.PLATON['IKOZAEDAR'],with_labels=True,node_color='y')

Bojanje vrhova grafa

Zadatak

U tablici se nalazi popis od 10 studentica zajedno s kolegijima koje su odabrale.

studentica  odabrani kolegiji
Marija Fizika, Matematika, Engleski
Janja Fizika, Geografija, Ekonomija
Ivana Geografija, Poslovanje
Ana Statistika, Ekonomija
Lana Matematika, Poslovanje
Sandra Fizika, Geografija
Danijela Poslovanje, Statistika
Katarina Matematika, Geografija
Petra Fizika, Plivanje, Statistika
Dijana Fizika, Ekonomija, Plivanje

Neki od kolegija se mogu istovremeno predavati. Međutim, želimo li svakoj od studentica omogućiti nesmetano slušanje svih kolegija koje je odabrala, koliko najmanje različitih vremenskih termina predavanja moramo staviti u raspored?

Rješenje

Formiramo graf u kojemu su vrhovi svi spomenuti kolegiji, a dva vrha su spojena bridom ako i samo ako postoji studentica koja je upisala oba pripadna kolegija. Najmanji broj termina je tada jednak kromatskom broju tog grafa.

In [30]:
G1=nx.Graph({"fizika":["matematika","engleski","geografija","ekonomija","plivanje","statistika"], 
          "matematika":["engleski","poslovanje","geografija"], 
          "geografija":["ekonomija","poslovanje"], 
          "statistika":["ekonomija","poslovanje","plivanje"], 
          "ekonomija":["plivanje"]})
In [31]:
figure(figsize=(6.5,6.5))
nx.draw_circular(G1,with_labels=True,node_color='y',node_size=5000,edgecolors='k')

Kromatski broj grafa je 4 pa su potrebna najmanje 4 različita termina.

In [32]:
DSTG.kromatski_broj(G1)
Out[32]:
4

Jedan mogući razmještaj predmeta u termine (dva predmeta se izvode u istom terminu ako i samo ako imaju istu boju).

In [33]:
DSTG.bojanje_vrhova(G1)
Out[33]:
{'fizika': 0,
 'matematika': 1,
 'geografija': 2,
 'ekonomija': 1,
 'statistika': 2,
 'plivanje': 3,
 'poslovanje': 0,
 'engleski': 2}

želimo li to prikazati vizualno na samom grafu

In [34]:
figure(figsize=(6.5,6.5))
DSTG.obojani_vrhovi(G1,nx.circular_layout(G1),5000)

Lista svih kliki u grafu

In [35]:
list(nx.enumerate_all_cliques(G1))
Out[35]:
[['fizika'],
 ['matematika'],
 ['geografija'],
 ['statistika'],
 ['ekonomija'],
 ['engleski'],
 ['plivanje'],
 ['poslovanje'],
 ['fizika', 'matematika'],
 ['fizika', 'geografija'],
 ['fizika', 'statistika'],
 ['fizika', 'ekonomija'],
 ['fizika', 'engleski'],
 ['fizika', 'plivanje'],
 ['matematika', 'geografija'],
 ['matematika', 'engleski'],
 ['matematika', 'poslovanje'],
 ['geografija', 'ekonomija'],
 ['geografija', 'poslovanje'],
 ['statistika', 'ekonomija'],
 ['statistika', 'plivanje'],
 ['statistika', 'poslovanje'],
 ['ekonomija', 'plivanje'],
 ['fizika', 'matematika', 'geografija'],
 ['fizika', 'matematika', 'engleski'],
 ['fizika', 'geografija', 'ekonomija'],
 ['fizika', 'statistika', 'ekonomija'],
 ['fizika', 'statistika', 'plivanje'],
 ['fizika', 'ekonomija', 'plivanje'],
 ['matematika', 'geografija', 'poslovanje'],
 ['statistika', 'ekonomija', 'plivanje'],
 ['fizika', 'statistika', 'ekonomija', 'plivanje']]

Lista svih maksimalnih kliki

In [36]:
list(nx.find_cliques(G1))
Out[36]:
[['fizika', 'matematika', 'geografija'],
 ['fizika', 'matematika', 'engleski'],
 ['fizika', 'ekonomija', 'statistika', 'plivanje'],
 ['fizika', 'ekonomija', 'geografija'],
 ['poslovanje', 'statistika'],
 ['poslovanje', 'matematika', 'geografija']]

Ukupni broj svih maksimalnih kliki

In [37]:
nx.graph_number_of_cliques(G1)
Out[37]:
6

Veličina najveće klike

In [38]:
nx.graph_clique_number(G1)
Out[38]:
4

Veličine najvećih kliki koje sadrže pojedini vrh

In [39]:
nx.node_clique_number(G1)
Out[39]:
{'fizika': 4,
 'matematika': 3,
 'geografija': 3,
 'statistika': 4,
 'ekonomija': 4,
 'engleski': 3,
 'plivanje': 4,
 'poslovanje': 3}

Ukupni broj maksimalnih kliki po svakom vrhu

In [40]:
nx.number_of_cliques(G1)
Out[40]:
{'fizika': 4,
 'matematika': 3,
 'geografija': 3,
 'statistika': 2,
 'ekonomija': 2,
 'engleski': 1,
 'plivanje': 1,
 'poslovanje': 2}

Sve maksimalne klike koje sadrže zadani vrh

In [41]:
nx.cliques_containing_node(G1,['fizika','matematika'])
Out[41]:
{'fizika': [['fizika', 'matematika', 'geografija'],
  ['fizika', 'matematika', 'engleski'],
  ['fizika', 'ekonomija', 'statistika', 'plivanje'],
  ['fizika', 'ekonomija', 'geografija']],
 'matematika': [['fizika', 'matematika', 'geografija'],
  ['fizika', 'matematika', 'engleski'],
  ['poslovanje', 'matematika', 'geografija']]}

Pogledajmo malo kako se ponašaju algoritmi za pohlepno bojanje vrhova na zadanom grafu.

Pohlepno bojanje sa slučajnim rasporedom vrhova ne mora uvijek dati bojanje vrhova s minimalnim brojem boja.

In [42]:
for i in range(100):
    rj=nx.greedy_color(G1,'random_sequential')
    if max(rj.values())>3:
        print('korak: ',i)
        print(rj)
        break

korak:  9
{'plivanje': 0, 'poslovanje': 0, 'matematika': 1, 'fizika': 2, 'statistika': 1, 'geografija': 3, 'engleski': 0, 'ekonomija': 4}

Welsh-Powellov algoritam

In [43]:
nx.greedy_color(G1,'largest_first')
Out[43]:
{'fizika': 0,
 'matematika': 1,
 'geografija': 2,
 'statistika': 1,
 'ekonomija': 3,
 'plivanje': 2,
 'poslovanje': 0,
 'engleski': 2}

Brelazov algoritam

In [44]:
nx.greedy_color(G1,'DSATUR')
Out[44]:
{'fizika': 0,
 'matematika': 1,
 'geografija': 2,
 'ekonomija': 1,
 'statistika': 2,
 'plivanje': 3,
 'poslovanje': 0,
 'engleski': 2}

Zadatak

Devet televizijskih postaja je smješteno u devet gradova $A,$ $B,$ $C,$ $D,$ $E,$ $F,$ $G,$ $H,$ $I$ čije su međusobne udaljenosti u kilometrima dane u tablici.

  A B C D E F G H
B 85              
C 137 165            
D 123 39 205          
E 164 132 117 171        
F 105 75 235 92 201      
G 134 191 252 223 298 177    
H 114 77 113 117 54 147 247  
I 132 174 22 213 138 237 245 120

Svakoj televizijskoj postaji se treba dodijeliti kanal preko kojeg će emitirati svoj program. Zbog nesmetanog emitiranja programa, televizijskim postajama koje su na udaljenosti manjoj od 150 km treba dodijeliti različite kanale. Televizijske postaje koje su na udaljenosti većoj od 150 km mogu nesmetano emitirati svoje programe preko istog kanala.

  • Koliko je najmanje kanala potrebno kako bi sve televizijske postaje mogle nesmetano emitirati svoje programe? Problem modelirajte pomoću grafova. Opišite kratko i jasno svoj postupak modeliranja i sve svoje tvrdnje precizno obrazložite.

  • U grafu kojeg ste dobili u prethodnom dijelu zadatka pronađite jednu najveću kliku i ispitajte da li je taj graf planarni. Sve svoje tvrdnje precizno obrazložite.

Rješenje

Konstruiramo graf u kojemu će vrhovi biti televizijske postaje, a dvije televizijske postaje su spojene bridom ako i samo ako su na udaljenosti manjoj od 150 km. Tada je minimalni broj kanala jednak kromatskom broju konstruiranog grafa.

In [45]:
G2=nx.Graph({"A":["B","C","D","F","G","H","I"],"B":["D","E","F","H"],"C":["E","H","I"], 
          "D":["F","H"],"E":["H","I"],"F":["H"],"H":["I"]})
In [46]:
figure(figsize=(6.5,6.5))
nx.draw_circular(G2,with_labels=True,node_color='y',edgecolors='k')

Kromatski broj grafa je 5 pa je potrebno minimalno 5 različitih kanala.

In [47]:
DSTG.kromatski_broj(G2)
Out[47]:
5

Jedno bojanje vrhova s minimalnim brojem boja. Na istom kanalu mogu emitirati svoje programe one televizijske postaje kojima je dodijeljena ista boja.

In [48]:
DSTG.bojanje_vrhova(G2)
Out[48]:
{'A': 0, 'H': 1, 'B': 2, 'D': 3, 'F': 4, 'C': 2, 'I': 3, 'E': 0, 'G': 1}

želimo li to prikazati vizualno na samom grafu

In [49]:
figure(figsize=(6.5,6.5))
DSTG.obojani_vrhovi(G2,nx.circular_layout(G2))

Lista svih kliki u grafu

In [50]:
list(nx.enumerate_all_cliques(G2))
Out[50]:
[['A'],
 ['B'],
 ['C'],
 ['D'],
 ['E'],
 ['F'],
 ['H'],
 ['G'],
 ['I'],
 ['A', 'B'],
 ['A', 'C'],
 ['A', 'D'],
 ['A', 'F'],
 ['A', 'H'],
 ['A', 'G'],
 ['A', 'I'],
 ['B', 'D'],
 ['B', 'E'],
 ['B', 'F'],
 ['B', 'H'],
 ['C', 'E'],
 ['C', 'H'],
 ['C', 'I'],
 ['D', 'F'],
 ['D', 'H'],
 ['E', 'H'],
 ['E', 'I'],
 ['F', 'H'],
 ['H', 'I'],
 ['A', 'B', 'D'],
 ['A', 'B', 'F'],
 ['A', 'B', 'H'],
 ['A', 'C', 'H'],
 ['A', 'C', 'I'],
 ['A', 'D', 'F'],
 ['A', 'D', 'H'],
 ['A', 'F', 'H'],
 ['A', 'H', 'I'],
 ['B', 'D', 'F'],
 ['B', 'D', 'H'],
 ['B', 'E', 'H'],
 ['B', 'F', 'H'],
 ['C', 'E', 'H'],
 ['C', 'E', 'I'],
 ['C', 'H', 'I'],
 ['D', 'F', 'H'],
 ['E', 'H', 'I'],
 ['A', 'B', 'D', 'F'],
 ['A', 'B', 'D', 'H'],
 ['A', 'B', 'F', 'H'],
 ['A', 'C', 'H', 'I'],
 ['A', 'D', 'F', 'H'],
 ['B', 'D', 'F', 'H'],
 ['C', 'E', 'H', 'I'],
 ['A', 'B', 'D', 'F', 'H']]

Lista svih maksimalnih kliki

In [51]:
list(nx.find_cliques(G2))
Out[51]:
[['E', 'H', 'I', 'C'],
 ['E', 'H', 'B'],
 ['A', 'G'],
 ['A', 'H', 'D', 'F', 'B'],
 ['A', 'H', 'I', 'C']]

Ukupni broj svih maksimalnih kliki

In [52]:
nx.graph_number_of_cliques(G2)
Out[52]:
5

Veličina najveće klike

In [53]:
nx.graph_clique_number(G2)
Out[53]:
5

Veličine najvećih kliki koje sadrže pojedini vrh

In [54]:
nx.node_clique_number(G2)
Out[54]:
{'A': 5, 'B': 5, 'C': 4, 'D': 5, 'E': 4, 'F': 5, 'H': 5, 'G': 2, 'I': 4}

Ukupni broj maksimalnih kliki po svakom vrhu

In [55]:
nx.number_of_cliques(G2)
Out[55]:
{'A': 3, 'B': 2, 'C': 2, 'D': 1, 'E': 2, 'F': 1, 'H': 4, 'G': 1, 'I': 2}

Sve maksimalne klike koje sadrže zadani vrh

In [56]:
nx.cliques_containing_node(G2,['A','E','H'])
Out[56]:
{'A': [['A', 'G'], ['A', 'H', 'D', 'F', 'B'], ['A', 'H', 'I', 'C']],
 'E': [['E', 'H', 'I', 'C'], ['E', 'H', 'B']],
 'H': [['E', 'H', 'I', 'C'],
  ['E', 'H', 'B'],
  ['A', 'H', 'D', 'F', 'B'],
  ['A', 'H', 'I', 'C']]}

Promatrani graf nije planarni jer sadrži podgraf $K_5$ koji nije planarni.

In [57]:
nx.check_planarity(G2)
Out[57]:
(False, None)

Pogledajmo kako još pohlepna bojanja rade na promatranom grafu. Pokrenite implementirane algoritme za pohlepno bojanje na zadanom grafu 10 000 puta i obratite pažnju da li uvijek daju bojanje vrhova s minimalnim brojem boja.
Kako Welsh-Powellov i Brelazov algoritam nisu randomizirani u networkx modulu, koristimo vlastite implementacije koje su randomizirane.

In [58]:
for k in range(60):
    rj=nx.greedy_color(G2,'random_sequential')
    print(rj,max(rj.values())+1)

{'C': 0, 'B': 0, 'H': 1, 'G': 0, 'I': 2, 'F': 2, 'E': 3, 'A': 3, 'D': 4} 5
{'B': 0, 'C': 0, 'A': 1, 'E': 1, 'H': 2, 'D': 3, 'I': 3, 'F': 4, 'G': 0} 5
{'I': 0, 'G': 0, 'C': 1, 'E': 2, 'B': 0, 'H': 3, 'A': 2, 'D': 1, 'F': 4} 5
{'H': 0, 'E': 1, 'C': 2, 'I': 3, 'D': 1, 'G': 0, 'F': 2, 'B': 3, 'A': 4} 5
{'D': 0, 'H': 1, 'C': 0, 'A': 2, 'E': 2, 'G': 0, 'F': 3, 'B': 4, 'I': 3} 5
{'E': 0, 'H': 1, 'D': 0, 'F': 2, 'I': 2, 'A': 3, 'G': 0, 'B': 4, 'C': 4} 5
{'E': 0, 'I': 1, 'D': 0, 'C': 2, 'B': 1, 'A': 3, 'H': 4, 'G': 0, 'F': 2} 5
{'C': 0, 'B': 0, 'E': 1, 'F': 1, 'H': 2, 'D': 3, 'G': 0, 'I': 3, 'A': 4} 5
{'B': 0, 'I': 0, 'G': 0, 'H': 1, 'D': 2, 'F': 3, 'C': 2, 'A': 4, 'E': 3} 5
{'E': 0, 'H': 1, 'D': 0, 'C': 2, 'G': 0, 'I': 3, 'B': 2, 'A': 4, 'F': 3} 5
{'I': 0, 'H': 1, 'C': 2, 'G': 0, 'F': 0, 'E': 3, 'A': 3, 'B': 2, 'D': 4} 5
{'E': 0, 'G': 0, 'D': 0, 'B': 1, 'A': 2, 'I': 1, 'H': 3, 'F': 4, 'C': 4} 5
{'E': 0, 'B': 1, 'C': 1, 'G': 0, 'F': 0, 'A': 2, 'D': 3, 'I': 3, 'H': 4} 5
{'C': 0, 'D': 0, 'E': 1, 'H': 2, 'F': 1, 'G': 0, 'A': 3, 'B': 4, 'I': 4} 5
{'A': 0, 'H': 1, 'F': 2, 'D': 3, 'E': 0, 'G': 1, 'C': 2, 'B': 4, 'I': 3} 5
{'F': 0, 'D': 1, 'I': 0, 'C': 1, 'G': 0, 'E': 2, 'B': 3, 'H': 4, 'A': 2} 5
{'A': 0, 'D': 1, 'G': 1, 'E': 0, 'F': 2, 'B': 3, 'C': 1, 'H': 4, 'I': 2} 5
{'A': 0, 'G': 1, 'C': 1, 'H': 2, 'D': 1, 'E': 0, 'F': 3, 'I': 3, 'B': 4} 5
{'H': 0, 'G': 0, 'E': 1, 'B': 2, 'D': 1, 'I': 2, 'A': 3, 'C': 4, 'F': 4} 5
{'B': 0, 'H': 1, 'C': 0, 'D': 2, 'F': 3, 'A': 4, 'E': 2, 'I': 3, 'G': 0} 5
{'G': 0, 'I': 0, 'A': 1, 'D': 0, 'B': 2, 'E': 1, 'C': 2, 'F': 3, 'H': 4} 5
{'I': 0, 'A': 1, 'H': 2, 'F': 0, 'B': 3, 'D': 4, 'G': 0, 'E': 1, 'C': 3} 5
{'C': 0, 'E': 1, 'B': 0, 'A': 1, 'H': 2, 'I': 3, 'F': 3, 'G': 0, 'D': 4} 5
{'E': 0, 'A': 0, 'H': 1, 'B': 2, 'C': 2, 'I': 3, 'D': 3, 'G': 1, 'F': 4} 5
{'G': 0, 'B': 0, 'C': 0, 'D': 1, 'H': 2, 'A': 3, 'F': 4, 'I': 1, 'E': 3} 5
{'H': 0, 'E': 1, 'C': 2, 'A': 1, 'F': 2, 'G': 0, 'I': 3, 'B': 3, 'D': 4} 5
{'B': 0, 'F': 1, 'D': 2, 'C': 0, 'A': 3, 'E': 1, 'G': 0, 'H': 4, 'I': 2} 5
{'E': 0, 'H': 1, 'B': 2, 'G': 0, 'C': 2, 'F': 0, 'A': 3, 'D': 4, 'I': 4} 5
{'A': 0, 'H': 1, 'B': 2, 'F': 3, 'I': 2, 'D': 4, 'E': 0, 'G': 1, 'C': 3} 5
{'I': 0, 'G': 0, 'D': 0, 'A': 1, 'F': 2, 'E': 1, 'B': 3, 'H': 4, 'C': 2} 5
{'E': 0, 'D': 0, 'A': 1, 'H': 2, 'I': 3, 'C': 4, 'F': 3, 'B': 4, 'G': 0} 5
{'D': 0, 'H': 1, 'A': 2, 'G': 0, 'C': 0, 'E': 2, 'I': 3, 'F': 3, 'B': 4} 5
{'H': 0, 'I': 1, 'A': 2, 'B': 1, 'C': 3, 'D': 3, 'F': 4, 'E': 2, 'G': 0} 5
{'B': 0, 'I': 0, 'D': 1, 'C': 1, 'E': 2, 'H': 3, 'A': 2, 'F': 4, 'G': 0} 5
{'D': 0, 'F': 1, 'H': 2, 'E': 0, 'C': 1, 'A': 3, 'I': 4, 'B': 4, 'G': 0} 5
{'F': 0, 'D': 1, 'H': 2, 'E': 0, 'B': 3, 'I': 1, 'A': 4, 'G': 0, 'C': 3} 5
{'B': 0, 'I': 0, 'C': 1, 'F': 1, 'A': 2, 'G': 0, 'E': 2, 'H': 3, 'D': 4} 5
{'A': 0, 'D': 1, 'F': 2, 'E': 0, 'H': 3, 'I': 1, 'G': 1, 'C': 2, 'B': 4} 5
{'C': 0, 'D': 0, 'A': 1, 'E': 1, 'G': 0, 'B': 2, 'H': 3, 'I': 2, 'F': 4} 5
{'B': 0, 'I': 0, 'H': 1, 'A': 2, 'D': 3, 'F': 4, 'C': 3, 'E': 2, 'G': 0} 5
{'I': 0, 'C': 1, 'G': 0, 'E': 2, 'H': 3, 'F': 0, 'A': 2, 'B': 1, 'D': 4} 5
{'C': 0, 'B': 0, 'D': 1, 'A': 2, 'F': 3, 'E': 1, 'H': 4, 'G': 0, 'I': 3} 5
{'D': 0, 'A': 1, 'C': 0, 'G': 0, 'I': 2, 'E': 1, 'H': 3, 'F': 2, 'B': 4} 5
{'G': 0, 'H': 0, 'C': 1, 'F': 1, 'B': 2, 'D': 3, 'A': 4, 'E': 3, 'I': 2} 5
{'A': 0, 'D': 1, 'H': 2, 'C': 1, 'G': 1, 'B': 3, 'E': 0, 'F': 4, 'I': 3} 5
{'F': 0, 'E': 0, 'I': 1, 'C': 2, 'A': 3, 'D': 1, 'B': 2, 'H': 4, 'G': 0} 5
{'E': 0, 'I': 1, 'A': 0, 'H': 2, 'D': 1, 'B': 3, 'C': 3, 'G': 1, 'F': 4} 5
{'F': 0, 'D': 1, 'I': 0, 'G': 0, 'B': 2, 'H': 3, 'E': 1, 'A': 4, 'C': 2} 5
{'I': 0, 'B': 0, 'E': 1, 'H': 2, 'C': 3, 'F': 1, 'A': 4, 'G': 0, 'D': 3} 5
{'C': 0, 'F': 0, 'D': 1, 'E': 1, 'G': 0, 'A': 2, 'B': 3, 'H': 4, 'I': 3} 5
{'F': 0, 'I': 0, 'G': 0, 'C': 1, 'H': 2, 'A': 3, 'E': 3, 'B': 1, 'D': 4} 5
{'B': 0, 'I': 0, 'H': 1, 'F': 2, 'C': 2, 'D': 3, 'E': 3, 'A': 4, 'G': 0} 5
{'F': 0, 'C': 0, 'A': 1, 'H': 2, 'G': 0, 'E': 1, 'D': 3, 'I': 3, 'B': 4} 5
{'G': 0, 'F': 0, 'A': 1, 'B': 2, 'E': 0, 'D': 3, 'C': 2, 'I': 3, 'H': 4} 5
{'H': 0, 'A': 1, 'B': 2, 'F': 3, 'G': 0, 'C': 2, 'E': 1, 'I': 3, 'D': 4} 5
{'H': 0, 'A': 1, 'F': 2, 'G': 0, 'I': 2, 'B': 3, 'D': 4, 'E': 1, 'C': 3} 5
{'H': 0, 'A': 1, 'I': 2, 'C': 3, 'D': 2, 'E': 1, 'B': 3, 'G': 0, 'F': 4} 5
{'D': 0, 'G': 0, 'F': 1, 'C': 0, 'E': 1, 'A': 2, 'B': 3, 'I': 3, 'H': 4} 5
{'B': 0, 'H': 1, 'C': 0, 'A': 2, 'I': 3, 'D': 3, 'G': 0, 'E': 2, 'F': 4} 5
{'D': 0, 'B': 1, 'A': 2, 'I': 0, 'H': 3, 'E': 2, 'G': 0, 'F': 4, 'C': 1} 5
In [59]:
for k in range(20):
    print(DSTG.Welsh_Powell(G2))

(['A', 'H', 'B', 'E', 'C', 'F', 'I', 'D', 'G'], {'A': 1, 'H': 2, 'B': 3, 'E': 1, 'C': 3, 'F': 4, 'I': 4, 'D': 5, 'G': 2}, 5)
(['H', 'A', 'B', 'C', 'D', 'I', 'F', 'E', 'G'], {'H': 1, 'A': 2, 'B': 3, 'C': 3, 'D': 4, 'I': 4, 'F': 5, 'E': 2, 'G': 1}, 5)
(['H', 'A', 'B', 'I', 'F', 'D', 'C', 'E', 'G'], {'H': 1, 'A': 2, 'B': 3, 'I': 3, 'F': 4, 'D': 5, 'C': 4, 'E': 2, 'G': 1}, 5)
(['A', 'H', 'B', 'D', 'F', 'C', 'E', 'I', 'G'], {'A': 1, 'H': 2, 'B': 3, 'D': 4, 'F': 5, 'C': 3, 'E': 1, 'I': 4, 'G': 2}, 5)
(['H', 'A', 'B', 'I', 'F', 'D', 'E', 'C', 'G'], {'H': 1, 'A': 2, 'B': 3, 'I': 3, 'F': 4, 'D': 5, 'E': 2, 'C': 4, 'G': 1}, 5)
(['A', 'H', 'B', 'I', 'D', 'C', 'E', 'F', 'G'], {'A': 1, 'H': 2, 'B': 3, 'I': 3, 'D': 4, 'C': 4, 'E': 1, 'F': 5, 'G': 2}, 5)
(['H', 'A', 'B', 'I', 'C', 'F', 'E', 'D', 'G'], {'H': 1, 'A': 2, 'B': 3, 'I': 3, 'C': 4, 'F': 4, 'E': 2, 'D': 5, 'G': 1}, 5)
(['H', 'A', 'B', 'C', 'D', 'F', 'I', 'E', 'G'], {'H': 1, 'A': 2, 'B': 3, 'C': 3, 'D': 4, 'F': 5, 'I': 4, 'E': 2, 'G': 1}, 5)
(['H', 'A', 'B', 'E', 'F', 'I', 'D', 'C', 'G'], {'H': 1, 'A': 2, 'B': 3, 'E': 2, 'F': 4, 'I': 3, 'D': 5, 'C': 4, 'G': 1}, 5)
(['A', 'H', 'B', 'D', 'F', 'C', 'E', 'I', 'G'], {'A': 1, 'H': 2, 'B': 3, 'D': 4, 'F': 5, 'C': 3, 'E': 1, 'I': 4, 'G': 2}, 5)
(['H', 'A', 'B', 'E', 'D', 'I', 'C', 'F', 'G'], {'H': 1, 'A': 2, 'B': 3, 'E': 2, 'D': 4, 'I': 3, 'C': 4, 'F': 5, 'G': 1}, 5)
(['H', 'A', 'B', 'F', 'C', 'D', 'I', 'E', 'G'], {'H': 1, 'A': 2, 'B': 3, 'F': 4, 'C': 3, 'D': 5, 'I': 4, 'E': 2, 'G': 1}, 5)
(['H', 'A', 'B', 'I', 'D', 'F', 'E', 'C', 'G'], {'H': 1, 'A': 2, 'B': 3, 'I': 3, 'D': 4, 'F': 5, 'E': 2, 'C': 4, 'G': 1}, 5)
(['A', 'H', 'B', 'D', 'I', 'C', 'E', 'F', 'G'], {'A': 1, 'H': 2, 'B': 3, 'D': 4, 'I': 3, 'C': 4, 'E': 1, 'F': 5, 'G': 2}, 5)
(['H', 'A', 'B', 'I', 'E', 'F', 'C', 'D', 'G'], {'H': 1, 'A': 2, 'B': 3, 'I': 3, 'E': 2, 'F': 4, 'C': 4, 'D': 5, 'G': 1}, 5)
(['A', 'H', 'B', 'E', 'C', 'F', 'I', 'D', 'G'], {'A': 1, 'H': 2, 'B': 3, 'E': 1, 'C': 3, 'F': 4, 'I': 4, 'D': 5, 'G': 2}, 5)
(['A', 'H', 'B', 'I', 'C', 'D', 'E', 'F', 'G'], {'A': 1, 'H': 2, 'B': 3, 'I': 3, 'C': 4, 'D': 4, 'E': 1, 'F': 5, 'G': 2}, 5)
(['A', 'H', 'B', 'C', 'F', 'E', 'I', 'D', 'G'], {'A': 1, 'H': 2, 'B': 3, 'C': 3, 'F': 4, 'E': 1, 'I': 4, 'D': 5, 'G': 2}, 5)
(['A', 'H', 'B', 'F', 'E', 'I', 'D', 'C', 'G'], {'A': 1, 'H': 2, 'B': 3, 'F': 4, 'E': 1, 'I': 3, 'D': 5, 'C': 4, 'G': 2}, 5)
(['H', 'A', 'B', 'F', 'I', 'E', 'D', 'C', 'G'], {'H': 1, 'A': 2, 'B': 3, 'F': 4, 'I': 3, 'E': 2, 'D': 5, 'C': 4, 'G': 1}, 5)
In [60]:
for k in range(20):
    print(DSTG.Brelaz(G2))

(['H', 'B', 'E', 'F', 'A', 'D', 'I', 'C', 'G'], {'H': 1, 'B': 2, 'E': 3, 'F': 3, 'A': 4, 'D': 5, 'I': 2, 'C': 5, 'G': 1}, 5)
(['H', 'I', 'E', 'C', 'A', 'F', 'D', 'B', 'G'], {'H': 1, 'I': 2, 'E': 3, 'C': 4, 'A': 3, 'F': 2, 'D': 4, 'B': 5, 'G': 1}, 5)
(['A', 'I', 'H', 'C', 'E', 'F', 'B', 'D', 'G'], {'A': 1, 'I': 2, 'H': 3, 'C': 4, 'E': 1, 'F': 2, 'B': 4, 'D': 5, 'G': 2}, 5)
(['H', 'B', 'F', 'D', 'A', 'C', 'I', 'E', 'G'], {'H': 1, 'B': 2, 'F': 3, 'D': 4, 'A': 5, 'C': 2, 'I': 3, 'E': 4, 'G': 1}, 5)
(['A', 'C', 'H', 'I', 'E', 'F', 'B', 'D', 'G'], {'A': 1, 'C': 2, 'H': 3, 'I': 4, 'E': 1, 'F': 2, 'B': 4, 'D': 5, 'G': 2}, 5)
(['A', 'F', 'H', 'D', 'B', 'E', 'C', 'I', 'G'], {'A': 1, 'F': 2, 'H': 3, 'D': 4, 'B': 5, 'E': 1, 'C': 2, 'I': 4, 'G': 2}, 5)
(['H', 'E', 'B', 'F', 'D', 'A', 'I', 'C', 'G'], {'H': 1, 'E': 2, 'B': 3, 'F': 2, 'D': 4, 'A': 5, 'I': 3, 'C': 4, 'G': 1}, 5)
(['A', 'D', 'F', 'B', 'H', 'I', 'E', 'C', 'G'], {'A': 1, 'D': 2, 'F': 3, 'B': 4, 'H': 5, 'I': 2, 'E': 1, 'C': 3, 'G': 2}, 5)
(['H', 'C', 'E', 'I', 'A', 'D', 'B', 'F', 'G'], {'H': 1, 'C': 2, 'E': 3, 'I': 4, 'A': 3, 'D': 2, 'B': 4, 'F': 5, 'G': 1}, 5)
(['H', 'A', 'B', 'F', 'D', 'I', 'C', 'E', 'G'], {'H': 1, 'A': 2, 'B': 3, 'F': 4, 'D': 5, 'I': 3, 'C': 4, 'E': 2, 'G': 1}, 5)
(['A', 'C', 'I', 'H', 'E', 'F', 'B', 'D', 'G'], {'A': 1, 'C': 2, 'I': 3, 'H': 4, 'E': 1, 'F': 2, 'B': 3, 'D': 5, 'G': 2}, 5)
(['A', 'H', 'D', 'F', 'B', 'I', 'C', 'E', 'G'], {'A': 1, 'H': 2, 'D': 3, 'F': 4, 'B': 5, 'I': 3, 'C': 4, 'E': 1, 'G': 2}, 5)
(['H', 'B', 'D', 'F', 'A', 'E', 'C', 'I', 'G'], {'H': 1, 'B': 2, 'D': 3, 'F': 4, 'A': 5, 'E': 3, 'C': 2, 'I': 4, 'G': 1}, 5)
(['A', 'G', 'C', 'H', 'I', 'E', 'F', 'D', 'B'], {'A': 1, 'G': 2, 'C': 2, 'H': 3, 'I': 4, 'E': 1, 'F': 2, 'D': 4, 'B': 5}, 5)
(['H', 'A', 'F', 'B', 'D', 'E', 'C', 'I', 'G'], {'H': 1, 'A': 2, 'F': 3, 'B': 4, 'D': 5, 'E': 2, 'C': 3, 'I': 4, 'G': 1}, 5)
(['H', 'B', 'A', 'D', 'F', 'E', 'I', 'C', 'G'], {'H': 1, 'B': 2, 'A': 3, 'D': 4, 'F': 5, 'E': 3, 'I': 2, 'C': 4, 'G': 1}, 5)
(['H', 'F', 'B', 'A', 'D', 'C', 'E', 'I', 'G'], {'H': 1, 'F': 2, 'B': 3, 'A': 4, 'D': 5, 'C': 2, 'E': 4, 'I': 3, 'G': 1}, 5)
(['H', 'C', 'A', 'I', 'E', 'F', 'D', 'B', 'G'], {'H': 1, 'C': 2, 'A': 3, 'I': 4, 'E': 3, 'F': 2, 'D': 4, 'B': 5, 'G': 1}, 5)
(['H', 'F', 'D', 'B', 'A', 'C', 'I', 'E', 'G'], {'H': 1, 'F': 2, 'D': 3, 'B': 4, 'A': 5, 'C': 2, 'I': 3, 'E': 5, 'G': 1}, 5)
(['H', 'F', 'A', 'D', 'B', 'E', 'I', 'C', 'G'], {'H': 1, 'F': 2, 'A': 3, 'D': 4, 'B': 5, 'E': 2, 'I': 4, 'C': 5, 'G': 1}, 5)

Zadatak

Pokažite da Brelazov i Welsh-Powellov algoritam ne daju uvijek bojanje vrhova s minimalnim brojem boja u grafu

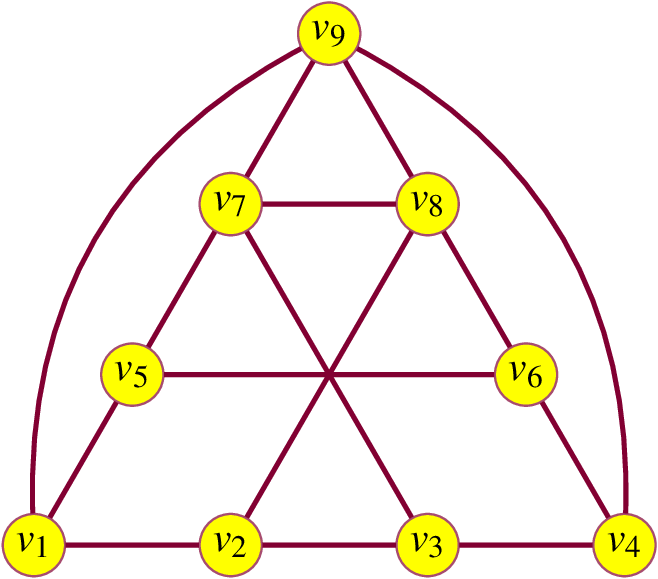
Rješenje

In [61]:
G3=nx.Graph({"v1":["v2","v5","v9"],"v2":["v3","v8"],"v3":["v4","v7"],"v4":["v6","v9"],
          "v5":["v6","v7"],"v6":["v8"],"v7":["v8","v9"],"v8":["v9"]})

Kromatski broj zadanog grafa je 3.

In [62]:
DSTG.kromatski_broj(G3)
Out[62]:
3

Vidimo da nam se dogodilo da u 20 izvođenja Brelazov i Welsh-Powellov algoritam nisu uvijek dali bojanje vrhova s minimalnim brojem boja (ukoliko se to ne dogodi u prvih 20 puta, ponovite algoritme više od 20 puta).

In [63]:
for k in range(20):
    print(DSTG.Welsh_Powell(G3))

(['v9', 'v8', 'v7', 'v4', 'v1', 'v5', 'v2', 'v6', 'v3'], {'v9': 1, 'v8': 2, 'v7': 3, 'v4': 2, 'v1': 2, 'v5': 1, 'v2': 1, 'v6': 3, 'v3': 4}, 4)
(['v9', 'v7', 'v8', 'v4', 'v3', 'v5', 'v6', 'v1', 'v2'], {'v9': 1, 'v7': 2, 'v8': 3, 'v4': 2, 'v3': 1, 'v5': 1, 'v6': 4, 'v1': 2, 'v2': 4}, 4)
(['v9', 'v7', 'v8', 'v2', 'v6', 'v5', 'v4', 'v1', 'v3'], {'v9': 1, 'v7': 2, 'v8': 3, 'v2': 1, 'v6': 1, 'v5': 3, 'v4': 2, 'v1': 2, 'v3': 3}, 3)
(['v8', 'v7', 'v9', 'v6', 'v3', 'v4', 'v5', 'v1', 'v2'], {'v8': 1, 'v7': 2, 'v9': 3, 'v6': 2, 'v3': 1, 'v4': 4, 'v5': 1, 'v1': 2, 'v2': 3}, 4)
(['v7', 'v8', 'v9', 'v2', 'v6', 'v1', 'v3', 'v4', 'v5'], {'v7': 1, 'v8': 2, 'v9': 3, 'v2': 1, 'v6': 1, 'v1': 2, 'v3': 2, 'v4': 4, 'v5': 3}, 4)
(['v7', 'v8', 'v9', 'v3', 'v1', 'v4', 'v6', 'v2', 'v5'], {'v7': 1, 'v8': 2, 'v9': 3, 'v3': 2, 'v1': 1, 'v4': 1, 'v6': 3, 'v2': 3, 'v5': 2}, 3)
(['v9', 'v8', 'v7', 'v3', 'v5', 'v4', 'v6', 'v2', 'v1'], {'v9': 1, 'v8': 2, 'v7': 3, 'v3': 1, 'v5': 1, 'v4': 2, 'v6': 3, 'v2': 3, 'v1': 2}, 3)
(['v8', 'v7', 'v9', 'v4', 'v1', 'v6', 'v3', 'v2', 'v5'], {'v8': 1, 'v7': 2, 'v9': 3, 'v4': 1, 'v1': 1, 'v6': 2, 'v3': 3, 'v2': 2, 'v5': 3}, 3)
(['v8', 'v7', 'v9', 'v6', 'v2', 'v1', 'v5', 'v4', 'v3'], {'v8': 1, 'v7': 2, 'v9': 3, 'v6': 2, 'v2': 2, 'v1': 1, 'v5': 3, 'v4': 1, 'v3': 3}, 3)
(['v8', 'v9', 'v7', 'v5', 'v6', 'v1', 'v3', 'v4', 'v2'], {'v8': 1, 'v9': 2, 'v7': 3, 'v5': 1, 'v6': 2, 'v1': 3, 'v3': 1, 'v4': 3, 'v2': 2}, 3)
(['v8', 'v9', 'v7', 'v3', 'v4', 'v6', 'v2', 'v1', 'v5'], {'v8': 1, 'v9': 2, 'v7': 3, 'v3': 1, 'v4': 3, 'v6': 2, 'v2': 2, 'v1': 1, 'v5': 4}, 4)
(['v8', 'v9', 'v7', 'v3', 'v5', 'v2', 'v4', 'v1', 'v6'], {'v8': 1, 'v9': 2, 'v7': 3, 'v3': 1, 'v5': 1, 'v2': 2, 'v4': 3, 'v1': 3, 'v6': 2}, 3)
(['v8', 'v9', 'v7', 'v3', 'v5', 'v2', 'v1', 'v4', 'v6'], {'v8': 1, 'v9': 2, 'v7': 3, 'v3': 1, 'v5': 1, 'v2': 2, 'v1': 3, 'v4': 3, 'v6': 2}, 3)
(['v7', 'v8', 'v9', 'v1', 'v3', 'v6', 'v2', 'v4', 'v5'], {'v7': 1, 'v8': 2, 'v9': 3, 'v1': 1, 'v3': 2, 'v6': 1, 'v2': 3, 'v4': 4, 'v5': 2}, 4)
(['v8', 'v9', 'v7', 'v4', 'v3', 'v2', 'v6', 'v5', 'v1'], {'v8': 1, 'v9': 2, 'v7': 3, 'v4': 1, 'v3': 2, 'v2': 3, 'v6': 2, 'v5': 1, 'v1': 4}, 4)
(['v9', 'v8', 'v7', 'v3', 'v6', 'v2', 'v1', 'v5', 'v4'], {'v9': 1, 'v8': 2, 'v7': 3, 'v3': 1, 'v6': 1, 'v2': 3, 'v1': 2, 'v5': 4, 'v4': 2}, 4)
(['v7', 'v9', 'v8', 'v6', 'v2', 'v3', 'v5', 'v4', 'v1'], {'v7': 1, 'v9': 2, 'v8': 3, 'v6': 1, 'v2': 1, 'v3': 2, 'v5': 2, 'v4': 3, 'v1': 3}, 3)
(['v8', 'v7', 'v9', 'v2', 'v1', 'v4', 'v6', 'v5', 'v3'], {'v8': 1, 'v7': 2, 'v9': 3, 'v2': 2, 'v1': 1, 'v4': 1, 'v6': 2, 'v5': 3, 'v3': 3}, 3)
(['v9', 'v8', 'v7', 'v5', 'v4', 'v1', 'v2', 'v3', 'v6'], {'v9': 1, 'v8': 2, 'v7': 3, 'v5': 1, 'v4': 2, 'v1': 2, 'v2': 1, 'v3': 4, 'v6': 3}, 4)
(['v7', 'v9', 'v8', 'v4', 'v2', 'v1', 'v6', 'v3', 'v5'], {'v7': 1, 'v9': 2, 'v8': 3, 'v4': 1, 'v2': 1, 'v1': 3, 'v6': 2, 'v3': 2, 'v5': 4}, 4)
In [64]:
for k in range(20):
    print(DSTG.Brelaz(G3))

(['v7', 'v8', 'v9', 'v2', 'v1', 'v5', 'v6', 'v4', 'v3'], {'v7': 1, 'v8': 2, 'v9': 3, 'v2': 1, 'v1': 2, 'v5': 3, 'v6': 1, 'v4': 2, 'v3': 3}, 3)
(['v8', 'v6', 'v4', 'v5', 'v1', 'v2', 'v3', 'v9', 'v7'], {'v8': 1, 'v6': 2, 'v4': 1, 'v5': 1, 'v1': 2, 'v2': 3, 'v3': 2, 'v9': 3, 'v7': 4}, 4)
(['v9', 'v1', 'v5', 'v6', 'v4', 'v8', 'v2', 'v3', 'v7'], {'v9': 1, 'v1': 2, 'v5': 1, 'v6': 2, 'v4': 3, 'v8': 3, 'v2': 1, 'v3': 2, 'v7': 4}, 4)
(['v9', 'v4', 'v3', 'v1', 'v2', 'v8', 'v7', 'v5', 'v6'], {'v9': 1, 'v4': 2, 'v3': 1, 'v1': 2, 'v2': 3, 'v8': 2, 'v7': 3, 'v5': 1, 'v6': 3}, 3)
(['v8', 'v9', 'v7', 'v4', 'v3', 'v2', 'v1', 'v5', 'v6'], {'v8': 1, 'v9': 2, 'v7': 3, 'v4': 1, 'v3': 2, 'v2': 3, 'v1': 1, 'v5': 2, 'v6': 3}, 3)
(['v7', 'v8', 'v9', 'v1', 'v2', 'v3', 'v4', 'v6', 'v5'], {'v7': 1, 'v8': 2, 'v9': 3, 'v1': 1, 'v2': 3, 'v3': 2, 'v4': 1, 'v6': 3, 'v5': 2}, 3)
(['v8', 'v7', 'v9', 'v5', 'v1', 'v2', 'v3', 'v4', 'v6'], {'v8': 1, 'v7': 2, 'v9': 3, 'v5': 1, 'v1': 2, 'v2': 3, 'v3': 1, 'v4': 2, 'v6': 3}, 3)
(['v9', 'v4', 'v1', 'v2', 'v3', 'v7', 'v8', 'v6', 'v5'], {'v9': 1, 'v4': 2, 'v1': 2, 'v2': 1, 'v3': 3, 'v7': 2, 'v8': 3, 'v6': 1, 'v5': 3}, 3)
(['v9', 'v7', 'v8', 'v1', 'v2', 'v3', 'v4', 'v6', 'v5'], {'v9': 1, 'v7': 2, 'v8': 3, 'v1': 2, 'v2': 1, 'v3': 3, 'v4': 2, 'v6': 1, 'v5': 3}, 3)
(['v8', 'v9', 'v7', 'v1', 'v5', 'v6', 'v4', 'v3', 'v2'], {'v8': 1, 'v9': 2, 'v7': 3, 'v1': 1, 'v5': 2, 'v6': 3, 'v4': 1, 'v3': 2, 'v2': 3}, 3)
(['v8', 'v7', 'v9', 'v3', 'v4', 'v6', 'v5', 'v1', 'v2'], {'v8': 1, 'v7': 2, 'v9': 3, 'v3': 1, 'v4': 2, 'v6': 3, 'v5': 1, 'v1': 2, 'v2': 3}, 3)
(['v9', 'v8', 'v7', 'v4', 'v3', 'v2', 'v1', 'v5', 'v6'], {'v9': 1, 'v8': 2, 'v7': 3, 'v4': 2, 'v3': 1, 'v2': 3, 'v1': 2, 'v5': 1, 'v6': 3}, 3)
(['v8', 'v6', 'v5', 'v1', 'v9', 'v2', 'v7', 'v3', 'v4'], {'v8': 1, 'v6': 2, 'v5': 1, 'v1': 2, 'v9': 3, 'v2': 3, 'v7': 2, 'v3': 1, 'v4': 4}, 4)
(['v9', 'v8', 'v7', 'v6', 'v5', 'v1', 'v2', 'v3', 'v4'], {'v9': 1, 'v8': 2, 'v7': 3, 'v6': 1, 'v5': 2, 'v1': 3, 'v2': 1, 'v3': 2, 'v4': 3}, 3)
(['v9', 'v1', 'v5', 'v6', 'v8', 'v7', 'v4', 'v3', 'v2'], {'v9': 1, 'v1': 2, 'v5': 1, 'v6': 2, 'v8': 3, 'v7': 2, 'v4': 3, 'v3': 1, 'v2': 4}, 4)
(['v7', 'v5', 'v6', 'v4', 'v3', 'v9', 'v8', 'v1', 'v2'], {'v7': 1, 'v5': 2, 'v6': 1, 'v4': 2, 'v3': 3, 'v9': 3, 'v8': 2, 'v1': 1, 'v2': 4}, 4)
(['v7', 'v5', 'v1', 'v8', 'v2', 'v3', 'v9', 'v4', 'v6'], {'v7': 1, 'v5': 2, 'v1': 1, 'v8': 2, 'v2': 3, 'v3': 2, 'v9': 3, 'v4': 1, 'v6': 3}, 3)
(['v9', 'v7', 'v8', 'v6', 'v5', 'v1', 'v2', 'v3', 'v4'], {'v9': 1, 'v7': 2, 'v8': 3, 'v6': 1, 'v5': 3, 'v1': 2, 'v2': 1, 'v3': 3, 'v4': 2}, 3)
(['v7', 'v3', 'v4', 'v8', 'v9', 'v6', 'v5', 'v1', 'v2'], {'v7': 1, 'v3': 2, 'v4': 1, 'v8': 2, 'v9': 3, 'v6': 3, 'v5': 2, 'v1': 1, 'v2': 3}, 3)
(['v9', 'v7', 'v8', 'v1', 'v2', 'v3', 'v4', 'v6', 'v5'], {'v9': 1, 'v7': 2, 'v8': 3, 'v1': 2, 'v2': 1, 'v3': 3, 'v4': 2, 'v6': 1, 'v5': 3}, 3)

Bojanje bridova grafa

Zadatak

Odredite kromatski i bridno kromatski broj grafa

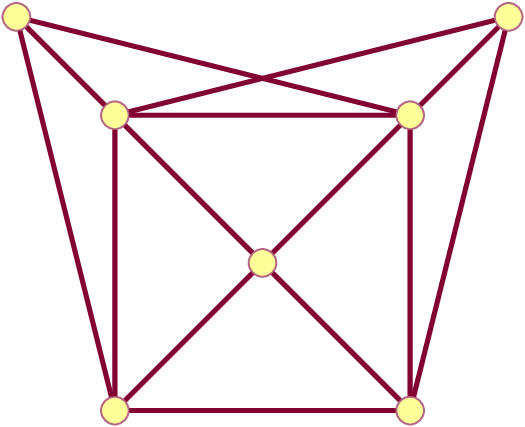
Rješenje

In [65]:
G4=nx.Graph({1:[2,4,5,6],2:[3,5,7],3:[4,5,6,7],4:[5,6,7]})
G4poz={1:[0,0],2:[3,0],3:[3,3],4:[0,3],5:[1.5,1.5],6:[-1,4],7:[4,4]}
In [66]:
nx.draw(G4,pos=G4poz,with_labels=True,node_color='y')

Kromatski broj grafa je 3.

In [67]:
DSTG.kromatski_broj(G4)
Out[67]:
3

Jedno bojanje vrhova s minimalnim brojem boja

In [68]:
DSTG.bojanje_vrhova(G4)
Out[68]:
{3: 0, 4: 1, 5: 2, 1: 0, 2: 1, 6: 2, 7: 2}
In [69]:
DSTG.obojani_vrhovi(G4,G4poz)

Pogledajmo kako se ponašaju pohlepna bojanja na ovom grafu. Izvršite svaki od tih algoritama 10 000 puta na zadanom grafu i donesite neki zaključak na temelju tog eksperimenta.

In [70]:
for k in range(20):
    rj=nx.greedy_color(G4,'random_sequential')
    print(rj,max(rj.values())+1)

{6: 0, 3: 1, 4: 2, 1: 1, 5: 0, 2: 2, 7: 0} 3
{5: 0, 2: 1, 4: 1, 7: 0, 6: 0, 1: 2, 3: 2} 3
{4: 0, 1: 1, 5: 2, 6: 2, 7: 1, 2: 0, 3: 3} 4
{2: 0, 1: 1, 5: 2, 7: 1, 4: 0, 3: 3, 6: 2} 4
{3: 0, 6: 1, 1: 0, 2: 1, 5: 2, 7: 2, 4: 3} 4
{1: 0, 2: 1, 6: 1, 4: 2, 7: 0, 3: 3, 5: 4} 5
{6: 0, 2: 0, 7: 1, 1: 1, 3: 2, 5: 3, 4: 4} 5
{3: 0, 2: 1, 4: 1, 5: 2, 6: 2, 7: 2, 1: 0} 3
{3: 0, 6: 1, 7: 1, 2: 2, 5: 1, 1: 0, 4: 2} 3
{7: 0, 2: 1, 1: 0, 3: 2, 4: 1, 6: 3, 5: 3} 4
{7: 0, 3: 1, 6: 0, 4: 2, 1: 1, 2: 2, 5: 0} 3
{3: 0, 7: 1, 6: 1, 1: 0, 5: 1, 2: 2, 4: 2} 3
{5: 0, 2: 1, 3: 2, 1: 2, 6: 0, 7: 0, 4: 1} 3
{5: 0, 4: 1, 1: 2, 3: 2, 7: 0, 6: 0, 2: 1} 3
{4: 0, 2: 0, 5: 1, 3: 2, 1: 2, 7: 1, 6: 1} 3
{4: 0, 2: 0, 1: 1, 5: 2, 7: 1, 6: 2, 3: 3} 4
{2: 0, 7: 1, 3: 2, 4: 0, 6: 1, 1: 2, 5: 1} 3
{1: 0, 7: 0, 5: 1, 3: 2, 4: 3, 6: 1, 2: 3} 4
{3: 0, 6: 1, 5: 1, 1: 0, 2: 2, 4: 2, 7: 1} 3
{4: 0, 7: 1, 3: 2, 2: 0, 5: 1, 1: 2, 6: 1} 3
In [71]:
for k in range(20):
    print(DSTG.Welsh_Powell(G4))

([3, 4, 1, 2, 5, 7, 6], {3: 1, 4: 2, 1: 1, 2: 2, 5: 3, 7: 3, 6: 3}, 3)
([3, 4, 5, 2, 1, 6, 7], {3: 1, 4: 2, 5: 3, 2: 2, 1: 1, 6: 3, 7: 3}, 3)
([4, 3, 1, 2, 5, 6, 7], {4: 1, 3: 2, 1: 2, 2: 1, 5: 3, 6: 3, 7: 3}, 3)
([3, 4, 1, 5, 2, 6, 7], {3: 1, 4: 2, 1: 1, 5: 3, 2: 2, 6: 3, 7: 3}, 3)
([4, 3, 2, 5, 1, 7, 6], {4: 1, 3: 2, 2: 1, 5: 3, 1: 2, 7: 3, 6: 3}, 3)
([4, 3, 1, 5, 2, 6, 7], {4: 1, 3: 2, 1: 2, 5: 3, 2: 1, 6: 3, 7: 3}, 3)
([3, 4, 5, 2, 1, 7, 6], {3: 1, 4: 2, 5: 3, 2: 2, 1: 1, 7: 3, 6: 3}, 3)
([4, 3, 1, 2, 5, 6, 7], {4: 1, 3: 2, 1: 2, 2: 1, 5: 3, 6: 3, 7: 3}, 3)
([3, 4, 2, 1, 5, 7, 6], {3: 1, 4: 2, 2: 2, 1: 1, 5: 3, 7: 3, 6: 3}, 3)
([3, 4, 2, 1, 5, 7, 6], {3: 1, 4: 2, 2: 2, 1: 1, 5: 3, 7: 3, 6: 3}, 3)
([3, 4, 5, 2, 1, 7, 6], {3: 1, 4: 2, 5: 3, 2: 2, 1: 1, 7: 3, 6: 3}, 3)
([4, 3, 1, 2, 5, 6, 7], {4: 1, 3: 2, 1: 2, 2: 1, 5: 3, 6: 3, 7: 3}, 3)
([4, 3, 5, 1, 2, 7, 6], {4: 1, 3: 2, 5: 3, 1: 2, 2: 1, 7: 3, 6: 3}, 3)
([3, 4, 5, 1, 2, 7, 6], {3: 1, 4: 2, 5: 3, 1: 1, 2: 2, 7: 3, 6: 3}, 3)
([4, 3, 2, 1, 5, 7, 6], {4: 1, 3: 2, 2: 1, 1: 2, 5: 3, 7: 3, 6: 3}, 3)
([4, 3, 5, 1, 2, 6, 7], {4: 1, 3: 2, 5: 3, 1: 2, 2: 1, 6: 3, 7: 3}, 3)
([3, 4, 2, 5, 1, 6, 7], {3: 1, 4: 2, 2: 2, 5: 3, 1: 1, 6: 3, 7: 3}, 3)
([4, 3, 1, 2, 5, 6, 7], {4: 1, 3: 2, 1: 2, 2: 1, 5: 3, 6: 3, 7: 3}, 3)
([3, 4, 2, 1, 5, 6, 7], {3: 1, 4: 2, 2: 2, 1: 1, 5: 3, 6: 3, 7: 3}, 3)
([4, 3, 1, 5, 2, 7, 6], {4: 1, 3: 2, 1: 2, 5: 3, 2: 1, 7: 3, 6: 3}, 3)
In [72]:
for k in range(20):
    print(DSTG.Brelaz(G4))

([3, 2, 7, 5, 1, 4, 6], {3: 1, 2: 2, 7: 3, 5: 3, 1: 1, 4: 2, 6: 3}, 3)
([4, 1, 6, 3, 7, 2, 5], {4: 1, 1: 2, 6: 3, 3: 2, 7: 3, 2: 1, 5: 3}, 3)
([3, 5, 2, 1, 4, 7, 6], {3: 1, 5: 2, 2: 3, 1: 1, 4: 3, 7: 2, 6: 2}, 3)
([3, 4, 6, 7, 1, 2, 5], {3: 1, 4: 2, 6: 3, 7: 3, 1: 1, 2: 2, 5: 3}, 3)
([3, 5, 2, 7, 1, 4, 6], {3: 1, 5: 2, 2: 3, 7: 2, 1: 1, 4: 3, 6: 2}, 3)
([3, 5, 4, 2, 1, 7, 6], {3: 1, 5: 2, 4: 3, 2: 3, 1: 1, 7: 2, 6: 2}, 3)
([3, 7, 4, 2, 5, 6, 1], {3: 1, 7: 2, 4: 3, 2: 3, 5: 2, 6: 2, 1: 1}, 3)
([3, 2, 7, 4, 5, 1, 6], {3: 1, 2: 2, 7: 3, 4: 2, 5: 3, 1: 1, 6: 3}, 3)
([3, 2, 7, 5, 1, 4, 6], {3: 1, 2: 2, 7: 3, 5: 3, 1: 1, 4: 2, 6: 3}, 3)
([3, 4, 7, 2, 5, 6, 1], {3: 1, 4: 2, 7: 3, 2: 2, 5: 3, 6: 3, 1: 1}, 3)
([3, 5, 4, 2, 6, 7, 1], {3: 1, 5: 2, 4: 3, 2: 3, 6: 2, 7: 2, 1: 1}, 3)
([4, 3, 7, 5, 2, 6, 1], {4: 1, 3: 2, 7: 3, 5: 3, 2: 1, 6: 3, 1: 2}, 3)
([4, 6, 1, 3, 7, 2, 5], {4: 1, 6: 2, 1: 3, 3: 3, 7: 2, 2: 1, 5: 2}, 3)
([4, 5, 3, 7, 1, 2, 6], {4: 1, 5: 2, 3: 3, 7: 2, 1: 3, 2: 1, 6: 2}, 3)
([4, 1, 5, 3, 7, 6, 2], {4: 1, 1: 2, 5: 3, 3: 2, 7: 3, 6: 3, 2: 1}, 3)
([4, 7, 3, 5, 2, 6, 1], {4: 1, 7: 2, 3: 3, 5: 2, 2: 1, 6: 2, 1: 3}, 3)
([3, 5, 2, 4, 1, 7, 6], {3: 1, 5: 2, 2: 3, 4: 3, 1: 1, 7: 2, 6: 2}, 3)
([3, 6, 4, 7, 1, 2, 5], {3: 1, 6: 2, 4: 3, 7: 2, 1: 1, 2: 3, 5: 2}, 3)
([3, 4, 5, 7, 2, 1, 6], {3: 1, 4: 2, 5: 3, 7: 3, 2: 2, 1: 1, 6: 3}, 3)
([4, 1, 5, 6, 2, 3, 7], {4: 1, 1: 2, 5: 3, 6: 3, 2: 1, 3: 2, 7: 3}, 3)

Bridno kromatski broj grafa je 5.

In [73]:
DSTG.bridno_kromatski_broj(G4)
Out[73]:
5

Jedno bojanje bridova s minimalnim brojem boja.

In [74]:
DSTG.bojanje_bridova(G4)
Out[74]:
{(3, 4): 0,
 (1, 4): 1,
 (4, 5): 2,
 (4, 6): 3,
 (4, 7): 4,
 (3, 5): 1,
 (3, 6): 2,
 (3, 7): 3,
 (2, 3): 4,
 (2, 5): 0,
 (1, 2): 2,
 (2, 7): 1,
 (1, 5): 3,
 (1, 6): 0}

Vizualizacija obojenih bridova na slici

In [75]:
DSTG.obojani_bridovi(G4,G4poz)

Implementirane algoritme za pohlepno bojanje vrhova grafa možemo primijeniti i za pohlepno bojanje bridova grafa. Ukoliko želimo pronaći neko pohlepno bojanje bridova grafa $G$, tada naše implementirane algoritme moramo primijeniti na linijskom grafu grafa $G$, tj. na grafu $L(G)$. Jasno, pohlepno bojanje bridova grafa općenito ne daje bojanje bridova s minimalnim brojem boja.

In [76]:
G4line=nx.line_graph(G4)

Ovdje je svaki od pohlepnih algoritama primijenjen samo 20 puta na promatranom grafu. Primijenite svaki od tih algoritama 10 000 puta na zadanom grafu i donesite na temelju toga neki zaključak.

In [77]:
for k in range(20):
    rj=nx.greedy_color(G4line,'random_sequential')
    print(rj,max(rj.values())+1)
    print()

{(1, 5): 0, (2, 5): 1, (1, 6): 1, (3, 4): 0, (1, 2): 2, (4, 7): 1, (3, 5): 2, (3, 7): 3, (3, 6): 4, (2, 7): 0, (2, 3): 5, (4, 5): 3, (1, 4): 4, (4, 6): 2} 6

{(4, 5): 0, (4, 6): 1, (4, 7): 2, (1, 4): 3, (2, 5): 1, (3, 4): 4, (3, 7): 0, (2, 7): 3, (2, 3): 2, (3, 6): 3, (1, 5): 2, (1, 6): 0, (3, 5): 5, (1, 2): 4} 6

{(3, 6): 0, (2, 7): 0, (1, 4): 0, (3, 4): 1, (2, 5): 1, (1, 2): 2, (1, 5): 3, (2, 3): 3, (1, 6): 1, (3, 7): 2, (4, 6): 2, (4, 5): 4, (3, 5): 5, (4, 7): 3} 6

{(4, 7): 0, (4, 6): 1, (2, 5): 0, (3, 5): 1, (3, 6): 0, (1, 4): 2, (1, 5): 3, (1, 6): 4, (2, 3): 2, (1, 2): 1, (2, 7): 3, (3, 4): 3, (3, 7): 4, (4, 5): 4} 5

{(4, 6): 0, (1, 5): 0, (1, 4): 1, (3, 5): 1, (1, 2): 2, (3, 7): 0, (2, 7): 1, (3, 6): 2, (3, 4): 3, (2, 3): 4, (1, 6): 3, (4, 5): 2, (4, 7): 4, (2, 5): 3} 5

{(2, 5): 0, (3, 4): 0, (4, 5): 1, (1, 5): 2, (1, 6): 0, (3, 7): 1, (1, 4): 3, (3, 5): 3, (2, 7): 2, (3, 6): 2, (4, 6): 4, (4, 7): 5, (2, 3): 4, (1, 2): 1} 6

{(3, 4): 0, (1, 5): 0, (4, 6): 1, (3, 7): 1, (2, 5): 1, (3, 6): 2, (3, 5): 3, (1, 6): 3, (2, 3): 4, (4, 7): 2, (4, 5): 4, (1, 2): 2, (1, 4): 5, (2, 7): 0} 6

{(1, 5): 0, (4, 5): 1, (1, 6): 1, (4, 6): 0, (2, 7): 0, (3, 6): 2, (3, 4): 3, (2, 3): 1, (2, 5): 2, (1, 4): 2, (3, 5): 4, (4, 7): 4, (1, 2): 3, (3, 7): 5} 6

{(2, 3): 0, (3, 6): 1, (1, 2): 1, (2, 5): 2, (3, 7): 2, (2, 7): 3, (4, 5): 0, (1, 4): 2, (1, 5): 3, (4, 7): 1, (4, 6): 3, (3, 5): 4, (3, 4): 5, (1, 6): 0} 6

{(3, 7): 0, (2, 3): 1, (4, 6): 0, (2, 7): 2, (1, 5): 0, (3, 6): 2, (1, 6): 1, (1, 4): 2, (1, 2): 3, (2, 5): 4, (3, 4): 3, (4, 5): 1, (3, 5): 5, (4, 7): 4} 6

{(2, 3): 0, (1, 4): 0, (2, 7): 1, (1, 2): 2, (1, 5): 1, (4, 6): 1, (4, 5): 2, (2, 5): 3, (3, 7): 2, (3, 4): 3, (3, 5): 4, (3, 6): 5, (4, 7): 4, (1, 6): 3} 6

{(3, 4): 0, (3, 5): 1, (3, 7): 2, (4, 6): 1, (3, 6): 3, (4, 7): 3, (1, 5): 0, (2, 5): 2, (1, 4): 2, (1, 2): 1, (2, 3): 4, (4, 5): 4, (2, 7): 0, (1, 6): 4} 5

{(2, 3): 0, (2, 7): 1, (1, 6): 0, (3, 7): 2, (3, 5): 1, (4, 6): 1, (2, 5): 2, (3, 6): 3, (1, 5): 3, (3, 4): 4, (4, 7): 0, (4, 5): 5, (1, 4): 2, (1, 2): 4} 6

{(1, 6): 0, (2, 3): 0, (4, 6): 1, (3, 7): 1, (4, 7): 0, (4, 5): 2, (1, 4): 3, (3, 5): 3, (3, 4): 4, (2, 5): 1, (1, 5): 4, (1, 2): 2, (2, 7): 3, (3, 6): 2} 5

{(4, 7): 0, (2, 3): 0, (1, 6): 0, (1, 4): 1, (3, 5): 1, (4, 6): 2, (3, 4): 3, (3, 6): 4, (1, 5): 2, (2, 5): 3, (4, 5): 4, (1, 2): 4, (3, 7): 2, (2, 7): 1} 5

{(1, 4): 0, (3, 5): 0, (3, 7): 1, (2, 3): 2, (2, 5): 1, (3, 4): 3, (4, 6): 1, (3, 6): 4, (1, 6): 2, (4, 5): 2, (1, 5): 3, (4, 7): 4, (1, 2): 4, (2, 7): 0} 5

{(4, 6): 0, (3, 6): 1, (2, 5): 0, (3, 7): 0, (2, 7): 1, (3, 5): 2, (1, 5): 1, (2, 3): 3, (3, 4): 4, (1, 6): 2, (4, 5): 3, (1, 4): 5, (4, 7): 2, (1, 2): 4} 6

{(4, 6): 0, (4, 5): 1, (1, 2): 0, (3, 4): 2, (3, 7): 0, (2, 3): 1, (4, 7): 3, (2, 7): 2, (2, 5): 3, (1, 6): 1, (1, 5): 2, (3, 5): 4, (1, 4): 4, (3, 6): 3} 5

{(4, 5): 0, (4, 6): 1, (4, 7): 2, (1, 5): 1, (1, 4): 3, (2, 5): 2, (3, 6): 0, (2, 7): 0, (1, 2): 4, (3, 4): 4, (3, 7): 1, (1, 6): 2, (2, 3): 3, (3, 5): 5} 6

{(3, 7): 0, (3, 4): 1, (3, 6): 2, (4, 7): 2, (1, 4): 0, (1, 6): 1, (4, 5): 3, (2, 7): 1, (4, 6): 4, (1, 5): 2, (2, 5): 0, (1, 2): 3, (3, 5): 4, (2, 3): 5} 6
In [78]:
for k in range(20):
    print(DSTG.Welsh_Powell(G4line))
    print()

([(3, 4), (1, 4), (2, 3), (3, 5), (4, 5), (4, 7), (1, 5), (3, 6), (2, 5), (1, 2), (4, 6), (3, 7), (2, 7), (1, 6)], {(3, 4): 1, (1, 4): 2, (2, 3): 2, (3, 5): 3, (4, 5): 4, (4, 7): 3, (1, 5): 1, (3, 6): 4, (2, 5): 5, (1, 2): 3, (4, 6): 5, (3, 7): 5, (2, 7): 1, (1, 6): 6}, 6)

([(3, 4), (4, 5), (3, 5), (2, 3), (1, 4), (4, 7), (1, 5), (3, 6), (1, 2), (3, 7), (4, 6), (2, 5), (1, 6), (2, 7)], {(3, 4): 1, (4, 5): 2, (3, 5): 3, (2, 3): 2, (1, 4): 3, (4, 7): 4, (1, 5): 1, (3, 6): 4, (1, 2): 4, (3, 7): 5, (4, 6): 5, (2, 5): 5, (1, 6): 2, (2, 7): 1}, 5)

([(3, 4), (2, 3), (1, 4), (3, 5), (4, 5), (3, 7), (3, 6), (1, 2), (1, 5), (4, 6), (4, 7), (2, 5), (2, 7), (1, 6)], {(3, 4): 1, (2, 3): 2, (1, 4): 2, (3, 5): 3, (4, 5): 4, (3, 7): 4, (3, 6): 5, (1, 2): 1, (1, 5): 5, (4, 6): 3, (4, 7): 5, (2, 5): 6, (2, 7): 3, (1, 6): 4}, 6)

([(3, 4), (4, 5), (3, 5), (2, 3), (1, 4), (4, 6), (1, 5), (4, 7), (2, 5), (1, 2), (3, 6), (3, 7), (1, 6), (2, 7)], {(3, 4): 1, (4, 5): 2, (3, 5): 3, (2, 3): 2, (1, 4): 3, (4, 6): 4, (1, 5): 1, (4, 7): 5, (2, 5): 4, (1, 2): 5, (3, 6): 5, (3, 7): 4, (1, 6): 2, (2, 7): 1}, 5)

([(3, 4), (4, 5), (3, 5), (1, 4), (2, 3), (1, 2), (3, 6), (3, 7), (4, 7), (1, 5), (4, 6), (2, 5), (1, 6), (2, 7)], {(3, 4): 1, (4, 5): 2, (3, 5): 3, (1, 4): 3, (2, 3): 2, (1, 2): 1, (3, 6): 4, (3, 7): 5, (4, 7): 4, (1, 5): 4, (4, 6): 5, (2, 5): 5, (1, 6): 2, (2, 7): 3}, 5)

([(3, 4), (1, 4), (3, 5), (2, 3), (4, 5), (3, 7), (1, 5), (2, 5), (4, 6), (1, 2), (3, 6), (4, 7), (2, 7), (1, 6)], {(3, 4): 1, (1, 4): 2, (3, 5): 2, (2, 3): 3, (4, 5): 3, (3, 7): 4, (1, 5): 1, (2, 5): 4, (4, 6): 4, (1, 2): 5, (3, 6): 5, (4, 7): 5, (2, 7): 1, (1, 6): 3}, 5)

([(3, 4), (1, 4), (3, 5), (4, 5), (2, 3), (1, 2), (1, 5), (4, 6), (3, 6), (4, 7), (3, 7), (2, 5), (1, 6), (2, 7)], {(3, 4): 1, (1, 4): 2, (3, 5): 2, (4, 5): 3, (2, 3): 3, (1, 2): 1, (1, 5): 4, (4, 6): 4, (3, 6): 5, (4, 7): 5, (3, 7): 4, (2, 5): 5, (1, 6): 3, (2, 7): 2}, 5)

([(3, 4), (2, 3), (3, 5), (4, 5), (1, 4), (4, 7), (1, 2), (4, 6), (3, 6), (2, 5), (1, 5), (3, 7), (1, 6), (2, 7)], {(3, 4): 1, (2, 3): 2, (3, 5): 3, (4, 5): 2, (1, 4): 3, (4, 7): 4, (1, 2): 1, (4, 6): 5, (3, 6): 4, (2, 5): 4, (1, 5): 5, (3, 7): 5, (1, 6): 2, (2, 7): 3}, 5)

([(3, 4), (3, 5), (4, 5), (2, 3), (1, 4), (4, 6), (2, 5), (3, 7), (3, 6), (1, 2), (4, 7), (1, 5), (2, 7), (1, 6)], {(3, 4): 1, (3, 5): 2, (4, 5): 3, (2, 3): 3, (1, 4): 2, (4, 6): 4, (2, 5): 1, (3, 7): 4, (3, 6): 5, (1, 2): 4, (4, 7): 5, (1, 5): 5, (2, 7): 2, (1, 6): 1}, 5)

([(3, 4), (2, 3), (1, 4), (3, 5), (4, 5), (4, 6), (2, 5), (3, 6), (1, 2), (3, 7), (1, 5), (4, 7), (1, 6), (2, 7)], {(3, 4): 1, (2, 3): 2, (1, 4): 2, (3, 5): 3, (4, 5): 4, (4, 6): 3, (2, 5): 1, (3, 6): 4, (1, 2): 3, (3, 7): 5, (1, 5): 5, (4, 7): 6, (1, 6): 1, (2, 7): 4}, 6)

([(3, 4), (2, 3), (3, 5), (4, 5), (1, 4), (3, 7), (1, 5), (4, 6), (2, 5), (1, 2), (3, 6), (4, 7), (2, 7), (1, 6)], {(3, 4): 1, (2, 3): 2, (3, 5): 3, (4, 5): 2, (1, 4): 3, (3, 7): 4, (1, 5): 1, (4, 6): 4, (2, 5): 4, (1, 2): 5, (3, 6): 5, (4, 7): 5, (2, 7): 1, (1, 6): 2}, 5)

([(3, 4), (2, 3), (4, 5), (3, 5), (1, 4), (1, 2), (3, 6), (3, 7), (1, 5), (4, 6), (4, 7), (2, 5), (1, 6), (2, 7)], {(3, 4): 1, (2, 3): 2, (4, 5): 2, (3, 5): 3, (1, 4): 3, (1, 2): 1, (3, 6): 4, (3, 7): 5, (1, 5): 4, (4, 6): 5, (4, 7): 4, (2, 5): 5, (1, 6): 2, (2, 7): 3}, 5)

([(3, 4), (1, 4), (4, 5), (2, 3), (3, 5), (3, 7), (4, 7), (4, 6), (1, 5), (3, 6), (1, 2), (2, 5), (1, 6), (2, 7)], {(3, 4): 1, (1, 4): 2, (4, 5): 3, (2, 3): 2, (3, 5): 4, (3, 7): 3, (4, 7): 4, (4, 6): 5, (1, 5): 1, (3, 6): 6, (1, 2): 3, (2, 5): 5, (1, 6): 4, (2, 7): 1}, 6)

([(3, 4), (1, 4), (4, 5), (2, 3), (3, 5), (3, 7), (4, 7), (1, 5), (1, 2), (4, 6), (3, 6), (2, 5), (2, 7), (1, 6)], {(3, 4): 1, (1, 4): 2, (4, 5): 3, (2, 3): 2, (3, 5): 4, (3, 7): 3, (4, 7): 4, (1, 5): 1, (1, 2): 3, (4, 6): 5, (3, 6): 6, (2, 5): 5, (2, 7): 1, (1, 6): 4}, 6)

([(3, 4), (1, 4), (4, 5), (3, 5), (2, 3), (1, 5), (1, 2), (3, 6), (4, 6), (3, 7), (2, 5), (4, 7), (2, 7), (1, 6)], {(3, 4): 1, (1, 4): 2, (4, 5): 3, (3, 5): 2, (2, 3): 3, (1, 5): 1, (1, 2): 4, (3, 6): 4, (4, 6): 5, (3, 7): 5, (2, 5): 5, (4, 7): 4, (2, 7): 1, (1, 6): 3}, 5)

([(3, 4), (2, 3), (1, 4), (3, 5), (4, 5), (2, 5), (3, 6), (3, 7), (1, 5), (4, 6), (1, 2), (4, 7), (1, 6), (2, 7)], {(3, 4): 1, (2, 3): 2, (1, 4): 2, (3, 5): 3, (4, 5): 4, (2, 5): 1, (3, 6): 4, (3, 7): 5, (1, 5): 5, (4, 6): 3, (1, 2): 3, (4, 7): 6, (1, 6): 1, (2, 7): 4}, 6)

([(3, 4), (1, 4), (4, 5), (3, 5), (2, 3), (4, 7), (4, 6), (2, 5), (3, 7), (1, 2), (3, 6), (1, 5), (2, 7), (1, 6)], {(3, 4): 1, (1, 4): 2, (4, 5): 3, (3, 5): 2, (2, 3): 3, (4, 7): 4, (4, 6): 5, (2, 5): 1, (3, 7): 5, (1, 2): 4, (3, 6): 4, (1, 5): 5, (2, 7): 2, (1, 6): 1}, 5)

([(3, 4), (1, 4), (3, 5), (2, 3), (4, 5), (1, 2), (4, 6), (3, 7), (3, 6), (2, 5), (4, 7), (1, 5), (2, 7), (1, 6)], {(3, 4): 1, (1, 4): 2, (3, 5): 2, (2, 3): 3, (4, 5): 3, (1, 2): 1, (4, 6): 4, (3, 7): 4, (3, 6): 5, (2, 5): 4, (4, 7): 5, (1, 5): 5, (2, 7): 2, (1, 6): 3}, 5)

([(3, 4), (1, 4), (2, 3), (4, 5), (3, 5), (3, 6), (1, 5), (4, 6), (3, 7), (2, 5), (1, 2), (4, 7), (2, 7), (1, 6)], {(3, 4): 1, (1, 4): 2, (2, 3): 2, (4, 5): 3, (3, 5): 4, (3, 6): 3, (1, 5): 1, (4, 6): 4, (3, 7): 5, (2, 5): 5, (1, 2): 3, (4, 7): 6, (2, 7): 1, (1, 6): 5}, 6)

([(3, 4), (3, 5), (1, 4), (4, 5), (2, 3), (4, 7), (1, 5), (1, 2), (4, 6), (2, 5), (3, 7), (3, 6), (2, 7), (1, 6)], {(3, 4): 1, (3, 5): 2, (1, 4): 2, (4, 5): 3, (2, 3): 3, (4, 7): 4, (1, 5): 1, (1, 2): 4, (4, 6): 5, (2, 5): 5, (3, 7): 5, (3, 6): 4, (2, 7): 1, (1, 6): 3}, 5)
In [79]:
for k in range(20):
    print(DSTG.Brelaz(G4line))
    print()

([(3, 4), (3, 5), (3, 7), (2, 3), (3, 6), (4, 5), (2, 5), (4, 6), (1, 5), (1, 4), (4, 7), (2, 7), (1, 2), (1, 6)], {(3, 4): 1, (3, 5): 2, (3, 7): 3, (2, 3): 4, (3, 6): 5, (4, 5): 3, (2, 5): 1, (4, 6): 2, (1, 5): 4, (1, 4): 5, (4, 7): 4, (2, 7): 2, (1, 2): 3, (1, 6): 1}, 5)

([(3, 4), (4, 7), (4, 6), (4, 5), (1, 4), (3, 6), (1, 6), (3, 5), (1, 5), (2, 3), (3, 7), (1, 2), (2, 7), (2, 5)], {(3, 4): 1, (4, 7): 2, (4, 6): 3, (4, 5): 4, (1, 4): 5, (3, 6): 2, (1, 6): 1, (3, 5): 3, (1, 5): 2, (2, 3): 4, (3, 7): 5, (1, 2): 3, (2, 7): 1, (2, 5): 5}, 5)

([(3, 4), (4, 6), (4, 5), (4, 7), (1, 4), (3, 5), (1, 5), (1, 6), (2, 5), (1, 2), (3, 7), (2, 3), (2, 7), (3, 6)], {(3, 4): 1, (4, 6): 2, (4, 5): 3, (4, 7): 4, (1, 4): 5, (3, 5): 2, (1, 5): 1, (1, 6): 3, (2, 5): 4, (1, 2): 2, (3, 7): 3, (2, 3): 5, (2, 7): 1, (3, 6): 4}, 5)

([(3, 4), (1, 4), (4, 7), (4, 6), (4, 5), (3, 5), (3, 6), (1, 6), (3, 7), (2, 3), (2, 7), (1, 5), (2, 5), (1, 2)], {(3, 4): 1, (1, 4): 2, (4, 7): 3, (4, 6): 4, (4, 5): 5, (3, 5): 2, (3, 6): 3, (1, 6): 1, (3, 7): 4, (2, 3): 5, (2, 7): 1, (1, 5): 3, (2, 5): 4, (1, 2): 6}, 6)

([(3, 4), (1, 4), (4, 7), (4, 5), (4, 6), (1, 6), (1, 5), (1, 2), (3, 5), (2, 5), (3, 7), (3, 6), (2, 3), (2, 7)], {(3, 4): 1, (1, 4): 2, (4, 7): 3, (4, 5): 4, (4, 6): 5, (1, 6): 1, (1, 5): 3, (1, 2): 4, (3, 5): 2, (2, 5): 1, (3, 7): 4, (3, 6): 3, (2, 3): 5, (2, 7): 2}, 5)

([(3, 4), (3, 7), (4, 7), (3, 6), (3, 5), (2, 3), (2, 7), (2, 5), (4, 5), (1, 4), (4, 6), (1, 6), (1, 5), (1, 2)], {(3, 4): 1, (3, 7): 2, (4, 7): 3, (3, 6): 3, (3, 5): 4, (2, 3): 5, (2, 7): 1, (2, 5): 2, (4, 5): 5, (1, 4): 2, (4, 6): 4, (1, 6): 1, (1, 5): 3, (1, 2): 4}, 5)

([(3, 4), (4, 6), (4, 7), (4, 5), (1, 4), (3, 6), (1, 6), (3, 5), (1, 5), (1, 2), (2, 3), (3, 7), (2, 7), (2, 5)], {(3, 4): 1, (4, 6): 2, (4, 7): 3, (4, 5): 4, (1, 4): 5, (3, 6): 3, (1, 6): 1, (3, 5): 2, (1, 5): 3, (1, 2): 2, (2, 3): 4, (3, 7): 5, (2, 7): 1, (2, 5): 5}, 5)

([(3, 4), (1, 4), (4, 5), (4, 7), (4, 6), (1, 6), (1, 5), (1, 2), (3, 5), (3, 7), (3, 6), (2, 3), (2, 5), (2, 7)], {(3, 4): 1, (1, 4): 2, (4, 5): 3, (4, 7): 4, (4, 6): 5, (1, 6): 1, (1, 5): 4, (1, 2): 3, (3, 5): 2, (3, 7): 3, (3, 6): 4, (2, 3): 5, (2, 5): 1, (2, 7): 2}, 5)

([(3, 4), (4, 6), (4, 7), (4, 5), (1, 4), (3, 5), (3, 7), (1, 5), (3, 6), (1, 6), (2, 3), (2, 5), (1, 2), (2, 7)], {(3, 4): 1, (4, 6): 2, (4, 7): 3, (4, 5): 4, (1, 4): 5, (3, 5): 2, (3, 7): 4, (1, 5): 1, (3, 6): 3, (1, 6): 4, (2, 3): 5, (2, 5): 3, (1, 2): 2, (2, 7): 1}, 5)

([(3, 4), (4, 7), (3, 7), (2, 3), (3, 5), (3, 6), (4, 5), (4, 6), (1, 4), (1, 5), (2, 5), (2, 7), (1, 2), (1, 6)], {(3, 4): 1, (4, 7): 2, (3, 7): 3, (2, 3): 2, (3, 5): 4, (3, 6): 5, (4, 5): 3, (4, 6): 4, (1, 4): 5, (1, 5): 1, (2, 5): 5, (2, 7): 1, (1, 2): 3, (1, 6): 2}, 5)

([(3, 4), (1, 4), (4, 5), (4, 6), (4, 7), (3, 6), (3, 7), (2, 3), (3, 5), (2, 7), (2, 5), (1, 5), (1, 2), (1, 6)], {(3, 4): 1, (1, 4): 2, (4, 5): 3, (4, 6): 4, (4, 7): 5, (3, 6): 2, (3, 7): 3, (2, 3): 4, (3, 5): 5, (2, 7): 1, (2, 5): 2, (1, 5): 1, (1, 2): 3, (1, 6): 5}, 5)

([(3, 4), (2, 3), (3, 6), (3, 7), (3, 5), (4, 6), (4, 7), (4, 5), (1, 4), (2, 5), (2, 7), (1, 5), (1, 6), (1, 2)], {(3, 4): 1, (2, 3): 2, (3, 6): 3, (3, 7): 4, (3, 5): 5, (4, 6): 2, (4, 7): 3, (4, 5): 4, (1, 4): 5, (2, 5): 1, (2, 7): 5, (1, 5): 2, (1, 6): 1, (1, 2): 3}, 5)

([(3, 4), (3, 5), (3, 6), (2, 3), (3, 7), (2, 5), (2, 7), (4, 7), (1, 2), (1, 5), (4, 5), (1, 4), (4, 6), (1, 6)], {(3, 4): 1, (3, 5): 2, (3, 6): 3, (2, 3): 4, (3, 7): 5, (2, 5): 1, (2, 7): 2, (4, 7): 3, (1, 2): 3, (1, 5): 4, (4, 5): 5, (1, 4): 2, (4, 6): 4, (1, 6): 1}, 5)

([(3, 4), (3, 6), (3, 5), (3, 7), (2, 3), (4, 7), (2, 7), (2, 5), (4, 5), (1, 4), (1, 2), (4, 6), (1, 6), (1, 5)], {(3, 4): 1, (3, 6): 2, (3, 5): 3, (3, 7): 4, (2, 3): 5, (4, 7): 2, (2, 7): 1, (2, 5): 2, (4, 5): 4, (1, 4): 3, (1, 2): 4, (4, 6): 5, (1, 6): 1, (1, 5): 5}, 5)

([(3, 4), (2, 3), (3, 6), (3, 5), (3, 7), (2, 7), (2, 5), (4, 5), (4, 6), (4, 7), (1, 4), (1, 2), (1, 5), (1, 6)], {(3, 4): 1, (2, 3): 2, (3, 6): 3, (3, 5): 4, (3, 7): 5, (2, 7): 1, (2, 5): 3, (4, 5): 2, (4, 6): 4, (4, 7): 3, (1, 4): 5, (1, 2): 4, (1, 5): 1, (1, 6): 2}, 5)

([(3, 4), (4, 7), (1, 4), (4, 5), (4, 6), (3, 6), (3, 5), (3, 7), (2, 3), (2, 5), (2, 7), (1, 2), (1, 5), (1, 6)], {(3, 4): 1, (4, 7): 2, (1, 4): 3, (4, 5): 4, (4, 6): 5, (3, 6): 2, (3, 5): 3, (3, 7): 4, (2, 3): 5, (2, 5): 1, (2, 7): 3, (1, 2): 2, (1, 5): 5, (1, 6): 1}, 5)

([(3, 4), (1, 4), (4, 7), (4, 5), (4, 6), (3, 5), (3, 6), (2, 3), (3, 7), (2, 7), (2, 5), (1, 2), (1, 5), (1, 6)], {(3, 4): 1, (1, 4): 2, (4, 7): 3, (4, 5): 4, (4, 6): 5, (3, 5): 2, (3, 6): 3, (2, 3): 4, (3, 7): 5, (2, 7): 1, (2, 5): 3, (1, 2): 5, (1, 5): 1, (1, 6): 4}, 5)

([(3, 4), (3, 7), (3, 5), (2, 3), (3, 6), (4, 7), (4, 6), (2, 7), (1, 4), (4, 5), (2, 5), (1, 5), (1, 6), (1, 2)], {(3, 4): 1, (3, 7): 2, (3, 5): 3, (2, 3): 4, (3, 6): 5, (4, 7): 3, (4, 6): 2, (2, 7): 1, (1, 4): 4, (4, 5): 5, (2, 5): 2, (1, 5): 1, (1, 6): 3, (1, 2): 5}, 5)

([(3, 4), (3, 7), (2, 3), (3, 5), (3, 6), (2, 7), (2, 5), (4, 5), (1, 5), (4, 7), (4, 6), (1, 4), (1, 2), (1, 6)], {(3, 4): 1, (3, 7): 2, (2, 3): 3, (3, 5): 4, (3, 6): 5, (2, 7): 1, (2, 5): 2, (4, 5): 3, (1, 5): 1, (4, 7): 4, (4, 6): 2, (1, 4): 5, (1, 2): 4, (1, 6): 3}, 5)

([(3, 4), (3, 6), (3, 7), (2, 3), (3, 5), (4, 7), (2, 7), (4, 5), (2, 5), (4, 6), (1, 4), (1, 2), (1, 6), (1, 5)], {(3, 4): 1, (3, 6): 2, (3, 7): 3, (2, 3): 4, (3, 5): 5, (4, 7): 2, (2, 7): 1, (4, 5): 3, (2, 5): 2, (4, 6): 4, (1, 4): 5, (1, 2): 3, (1, 6): 1, (1, 5): 4}, 5)

Zadatak

Osam studentica FOI-a treba posuditi određene knjige u knjižnici i svaku knjigu posuđuju na tjedan dana i pritom mogu posuditi samo jednu knjigu jer gradivo je zahtjevno i teško je dvije knjige proučiti u tjedan dana. U tablici je dani popis studentica kao i knjige koje su potrebne pojedinim studenticama.

studentica knjige
Emina $K_1$, $K_2$, $K_3$
Maja $K_2$, $K_4$, $K_5$, $K_6$
Ana $K_2$, $K_3$, $K_5$, $K_7$
Marina $K_3$, $K_5$
Sandra $K_1$, $K_6$, $K_7$
Sanja $K_2$, $K_4$, $K_6$
Martina $K_4$, $K_5$, $K_7$
Ines $K_3$, $K_6$

Nakon koliko minimalno tjedana će sve studentice posuditi sve knjige koje trebaju? Napravite za svaku studenticu jedan takav raspored posuđivanja knjiga po tjednima koji traje minimalni broj tjedana. Pritom pretpostavljamo da knjižnica ima samo po jedan primjerak pojedine knjige.

Rješenje

Konstruiramo bipartitni graf. U jednoj particiji su studentice, a u drugoj knjige. Pojedina studentica je spojena bridovima sa svim knjigama koje treba. Minimalni broj tjedana je tada jednak bridno kromatskom broju grafa. Svaka boja predstavlja tjedne.

In [80]:
G5=nx.Graph({"Emina":["K1","K2","K3"],"Maja":["K2","K4","K5","K6"], 
          "Ana":["K2","K3","K5","K7"],"Marina":["K3","K5"], 
          "Sandra":["K1","K6","K7"],"Sanja":["K2","K4","K6"], 
          "Martina":["K4","K5","K7"],"Ines":["K3","K6"]})
G5pos=nx.bipartite_layout(G5,nx.bipartite.sets(G5)[0],align='horizontal')
In [81]:
figure(figsize=(8,5))
nx.draw(G5,G5pos,with_labels=True,node_color='y',node_size=2000)

Bridno kromatski broj grafa je jednak 4 pa će nakon minimalno 4 tjedna sve studentice posuditi sve knjige koje trebaju.

In [82]:
DSTG.bridno_kromatski_broj(G5)
Out[82]:
4

jedno bojanje bridova s minimalnim brojem boja

In [83]:
DSTG.bojanje_bridova(G5)
Out[83]:
{('K2', 'Maja'): 0,
 ('K5', 'Maja'): 1,
 ('K6', 'Maja'): 2,
 ('K4', 'Maja'): 3,
 ('Ana', 'K2'): 1,
 ('Emina', 'K2'): 2,
 ('K2', 'Sanja'): 3,
 ('K6', 'Sanja'): 0,
 ('K6', 'Sandra'): 1,
 ('Ines', 'K6'): 3,
 ('K4', 'Sanja'): 1,
 ('K4', 'Martina'): 0,
 ('K5', 'Martina'): 2,
 ('Ana', 'K5'): 0,
 ('K5', 'Marina'): 3,
 ('Ana', 'K3'): 2,
 ('Ana', 'K7'): 3,
 ('K7', 'Martina'): 1,
 ('K3', 'Marina'): 0,
 ('Ines', 'K3'): 1,
 ('Emina', 'K3'): 3,
 ('K7', 'Sandra'): 0,
 ('Emina', 'K1'): 0,
 ('K1', 'Sandra'): 2}

Vizualizacija bojanja bridova na slici

In [84]:
figure(figsize=(8,5))
DSTG.obojani_bridovi(G5,G5pos,velicina_vrha=2000)

termini posuđivanja knjiga po tjednima (uzmemo po želji koja će boja predstavljati pojedini tjedan)

In [85]:
DSTG.raspored_termina(G5,["1. tjedan","2. tjedan","3. tjedan","4. tjedan"])
Out[85]:
 MartinaMarinaSandraEminaInesAnaSanjaMaja
1. tjedanK4K3K7K1 K5K6K2
2. tjedanK7 K6 K3K2K4K5
3. tjedanK5 K1K2 K3 K6
4. tjedan K5 K3K6K7K2K4
In [86]:
DSTG.raspored_termina(G5,["1. tjedan","2. tjedan","3. tjedan","4. tjedan"],permutacija=[3,2,1,4])
Out[86]:
 MartinaMarinaSandraEminaInesAnaSanjaMaja
1. tjedanK5 K1K2 K3 K6
2. tjedanK7 K6 K3K2K4K5
3. tjedanK4K3K7K1 K5K6K2
4. tjedan K5 K3K6K7K2K4

Želimo li raspored po knjigama, tj. da znamo kod koje se studentice u pojedinom tjednu nalazi pojedina knjiga

In [87]:
DSTG.raspored_termina(G5,["1. tjedan","2. tjedan","3. tjedan","4. tjedan"],2)
Out[87]:
 K5K2K4K6K3K7K1
1. tjedanAnaMajaMartinaSanjaMarinaSandraEmina
2. tjedanMajaAnaSanjaSandraInesMartina 
3. tjedanMartinaEmina MajaAna Sandra
4. tjedanMarinaSanjaMajaInesEminaAna 
In [88]:
DSTG.raspored_termina(G5,["1. tjedan","2. tjedan","3. tjedan","4. tjedan"],2,[3,4,2,1])
Out[88]:
 K5K2K4K6K3K7K1
1. tjedanMarinaSanjaMajaInesEminaAna 
2. tjedanMartinaEmina MajaAna Sandra
3. tjedanAnaMajaMartinaSanjaMarinaSandraEmina
4. tjedanMajaAnaSanjaSandraInesMartina 

Zadatak

Želimo izraditi raspored posjeta pacijenata $P=\{u,v,z,x\}$ koji se trebaju pregledati kod specijalista $S=\{a,b,c,d,e,f,g\}$. Pri tome pacijent treba posjetiti određenog specijalistu kako je dano u tablici susjednosti.

♦ $a$ $b$ $c$ $d$ $e$ $f$ $g$
$u$ 1 1 0 0 0 0 1
$v$ 0 1 1 0 1 0 0
$z$ 1 0 0 1 0 1 0
$x$ 0 0 0 0 1 1 1

Treba napraviti raspored posjeta pacijenata pojedinom specijalistu, ali i raspored za specijaliste da znaju u kojem terminu im dolazi pojedini pacijent. Svaki pregled traje pola sata i počinje se s radom u 8:00h.

Rješenje

Konstruiramo bipartitni graf. U jednoj particiji su pacijenti, a u drugoj specijalisti. Pojedini pacijent je spojena bridovima sa svim specijalistima koje treba posjetiti. Minimalni broj termina je tada jednak bridno kromatskom broju grafa. Svaka boja predstavlja pojedini termin od pola sata.

In [89]:
G6=nx.Graph({"u":["a","b","g"],"v":["b","c","e"],"z":["a","d","f"],"x":["e","f","g"]})
G6pos=nx.bipartite_layout(G6,nx.bipartite.sets(G6)[0],align='horizontal')
In [90]:
nx.draw(G6,G6pos,with_labels=True,node_color='y')

Bridno kromatski broj grafa je jednak 3 pa su potrebna minimalno tri različita termina u rasporedu.

In [91]:
DSTG.bridno_kromatski_broj(G6)
Out[91]:
3

jedno bojanje bridova s minimalnim brojem boja

In [92]:
DSTG.bojanje_bridova(G6)
Out[92]:
{('b', 'v'): 0,
 ('e', 'v'): 1,
 ('c', 'v'): 2,
 ('b', 'u'): 1,
 ('a', 'u'): 0,
 ('g', 'u'): 2,
 ('a', 'z'): 1,
 ('f', 'z'): 0,
 ('d', 'z'): 2,
 ('e', 'x'): 0,
 ('g', 'x'): 1,
 ('f', 'x'): 2}

Vizualizacija bojanja bridova na slici

In [93]:
DSTG.obojani_bridovi(G6,G6pos)

jedan mogući raspored termina za liječnike

In [94]:
DSTG.raspored_termina(G6,["8:00h","8:30h","9:00h"],2)
Out[94]:
 bdegcfa
8:00hv x  zu
8:30hu vx  z
9:00h z uvx 

jedan mogući raspored termina za pacijente

In [95]:
DSTG.raspored_termina(G6,["8:00h","8:30h","9:00h"])
Out[95]:
 xzvu
8:00hefba
8:30hgaeb
9:00hfdcg

možemo malo promijeniti termine

In [96]:
DSTG.raspored_termina(G6,["8:00h","8:30h","9:00h"],2,[2,3,1])
Out[96]:
 bdegcfa
8:00h z uvx 
8:30hv x  zu
9:00hu vx  z
In [97]:
DSTG.raspored_termina(G6,["8:00h","8:30h","9:00h"],1,[2,3,1])
Out[97]:
 xzvu
8:00hfdcg
8:30hefba
9:00hgaeb

Sparivanje u grafovima

Zadatak

Pet neudatih djevojaka ima određeni broj neoženjenih prijatelja kako je prikazano u sljedećoj tablici.

djevojke neoženjeni prijatelji
Sandra Ivan, Miroslav, Marijan, Danijel
Maja Miroslav, Franjo
Ana Ivan, Marijan
Emina Marijan, Danijel
Ines Miroslav, Marijan
  • Svaka se djevojka želi udati za nekog od svojih prijatelja. Da li je moguće svakoj od djevojaka ostvariti njihove želje? Ukoliko je to moguće, pronađite način kako to ostvariti. Ako je nemoguće ispuniti želju svakoj od djevojaka, objasnite zašto to nije moguće. Problem modelirajte pomoću grafova i objasnite svaku svoju tvrdnju.

  • Zamislimo ovakvu situaciju. Maja se želi udati za svojeg prijatelja Miroslava i trudi se da ga osvoji. Pretpostavimo da joj je to uspjelo i da ju je Miroslav oženio. Da li je na taj način Maja unesrećila neku od preostalih djevojaka u smislu da se ta djevojka nije mogla udati za nekog od svojih prijatelja? Da li je moguće u toj situaciji spasiti preostale djevojke osim Sandre tako da se svaka od njih uda za nekog od svojih prijatelja? Koje bi mogućnosti u tom slučaju imala Sandra? Obrazložite jasno i precizno svaki svoj odgovor.

Rješenje

Konstruiramo bipartitni graf. U jednoj particiji su djevojke, a u drugoj neoženjeni prijatelji. Svaka djevojka je u grafu susjedna samo sa svojim prijateljima.

In [98]:
G7=nx.Graph({"Sandra":["Ivan","Miroslav","Marijan","Danijel"],"Maja":["Miroslav","Franjo"], 
          "Ana":["Ivan","Marijan"],"Emina":["Marijan","Danijel"],"Ines":["Miroslav","Marijan"]})
G7pos=nx.bipartite_layout(G7,nx.bipartite.sets(G7)[0],align='horizontal')
In [99]:
nx.draw(G7,G7pos,with_labels=True,node_color='y',node_size=2800)

Moguće je svakoj djevojci ostvariti njezinu želju zato jer najveće sparivanje u promatranom bipartitnom grafu ima ukupno 5 bridova pa je to ujedno i savršeno sparivanje.

In [100]:
nx.max_weight_matching(G7, maxcardinality=True)
Out[100]:
{('Danijel', 'Sandra'),
 ('Franjo', 'Maja'),
 ('Ines', 'Miroslav'),
 ('Ivan', 'Ana'),
 ('Marijan', 'Emina')}

najveće sparivanje prikazano na grafu

In [101]:
figure(figsize=(10,6))
DSTG.najvece_sparivanje_graf(G7,G7pos,velicina_vrha=2800)

neko maksimalno sparivanje (koje nije najveće)

In [102]:
nx.maximal_matching(G7)
Out[102]:
{('Ana', 'Marijan'),
 ('Emina', 'Danijel'),
 ('Maja', 'Miroslav'),
 ('Sandra', 'Ivan')}

Neko na slučajni način odabrano maksimalno sparivanje na grafu

In [103]:
figure(figsize=(10,6))
DSTG.maksimalno_sparivanje_graf(G7,G7pos,velicina_vrha=2800)

Neko maksimalno sparivanje na grafu koje sadrži brid ('Maja','Miroslav')

In [104]:
figure(figsize=(10,6))
DSTG.maksimalno_sparivanje_graf(G7,G7pos,M=[('Maja','Miroslav')],velicina_vrha=2800)

drugi dio zadatka

Ako se Maja udala za Miroslava, tada će Franjo sigurno ostati neoženjen jer se on jedino sviđao Maji. Dakle, Maja će svojom udajom za Miroslava, sigurno unesrećiti neku od preostalih djevojaka u smislu da se neka od njih neće moći udati za neku od svojih simpatija.

Ukoliko se Maja uda za Miroslava, preostale djevojke osim Sandre je moguće spasiti na sljedeći način: Ines se udaje za Marijana, Emina za Danijela, Ana za Ivana. U tom slučaju Sandra ima mogućnost da se uda za Franju (iako on nije njezina simpatija) ili može ostati slobodna cura. :-)

Isprobajmo i našu funkciju random_maximal_matching koja će tražiti maksimalno sparivanje koje sadrži brid {Maja, Miroslav}. Vidimo da u 20 pokretanja ove funkcije čak možemo i dvije djevojke razočarati, tj. postoji maksimalno sparivanje sa samo tri brida koje sadrži brid {Maja, Miroslav}. Nadalje, moguće je da u svakom od tih maksimalnih sparivanja Sandra nikad nije razočarana. Naime, postoji puno bridova s kojima je Sandra susjedna pa je zato i velika vjerojatnost da će naša randomizirana funkcija odabrati ranije neki od tih bridova.

In [105]:
for k in range(20):
    print(DSTG.random_maximal_matching(G7,[('Maja','Miroslav')]))

[('Maja', 'Miroslav'), ('Sandra', 'Ivan'), ('Emina', 'Danijel'), ('Ines', 'Marijan')]
[('Maja', 'Miroslav'), ('Sandra', 'Marijan'), ('Ana', 'Ivan'), ('Emina', 'Danijel')]
[('Maja', 'Miroslav'), ('Ana', 'Marijan'), ('Emina', 'Danijel'), ('Sandra', 'Ivan')]
[('Maja', 'Miroslav'), ('Sandra', 'Ivan'), ('Emina', 'Marijan')]
[('Maja', 'Miroslav'), ('Ana', 'Ivan'), ('Ines', 'Marijan'), ('Sandra', 'Danijel')]
[('Maja', 'Miroslav'), ('Sandra', 'Danijel'), ('Emina', 'Marijan'), ('Ana', 'Ivan')]
[('Maja', 'Miroslav'), ('Sandra', 'Danijel'), ('Ines', 'Marijan'), ('Ana', 'Ivan')]
[('Maja', 'Miroslav'), ('Sandra', 'Danijel'), ('Ines', 'Marijan'), ('Ana', 'Ivan')]
[('Maja', 'Miroslav'), ('Sandra', 'Danijel'), ('Ines', 'Marijan'), ('Ana', 'Ivan')]
[('Maja', 'Miroslav'), ('Ana', 'Marijan'), ('Sandra', 'Danijel')]
[('Maja', 'Miroslav'), ('Emina', 'Marijan'), ('Sandra', 'Danijel'), ('Ana', 'Ivan')]
[('Maja', 'Miroslav'), ('Ines', 'Marijan'), ('Sandra', 'Ivan'), ('Emina', 'Danijel')]
[('Maja', 'Miroslav'), ('Ana', 'Ivan'), ('Emina', 'Marijan'), ('Sandra', 'Danijel')]
[('Maja', 'Miroslav'), ('Emina', 'Danijel'), ('Ana', 'Ivan'), ('Ines', 'Marijan')]
[('Maja', 'Miroslav'), ('Ana', 'Marijan'), ('Sandra', 'Ivan'), ('Emina', 'Danijel')]
[('Maja', 'Miroslav'), ('Emina', 'Marijan'), ('Sandra', 'Ivan')]
[('Maja', 'Miroslav'), ('Ines', 'Marijan'), ('Sandra', 'Ivan'), ('Emina', 'Danijel')]
[('Maja', 'Miroslav'), ('Sandra', 'Danijel'), ('Ines', 'Marijan'), ('Ana', 'Ivan')]
[('Maja', 'Miroslav'), ('Sandra', 'Marijan'), ('Ana', 'Ivan'), ('Emina', 'Danijel')]
[('Maja', 'Miroslav'), ('Sandra', 'Marijan'), ('Emina', 'Danijel'), ('Ana', 'Ivan')]

Ako nam se ne pojavi maksimalno sparivanje bez Sandre koje sadrži brid {Maja, Miroslav} u prvih 20 pokretanja, možemo probati algoritam pokrenuti više od 20 puta i čekati tako dugo dok se eventualno ne pojavi takvo sparivanje.

In [106]:
for k in range(100):
    spar=DSTG.random_maximal_matching(G7,[('Maja','Miroslav')])
    prvi=map(lambda x:x[0],spar)
    drugi=map(lambda x:x[1],spar)
    if not(('Sandra' in prvi) or ('Sandra' in drugi)):
        print(k+1,'. korak',spar)
        break
    elif k==99:
        print('Sandra ne odustaje od udaje. :-)')

14 . korak [('Maja', 'Miroslav'), ('Ana', 'Ivan'), ('Ines', 'Marijan'), ('Emina', 'Danijel')]

ili još bolje, izbrišemo sve bridove koji su susjedni sa vrhom 'Sandra' i tada relativno brzo dobijemo željeno sparivanje

In [107]:
bridoviSandra=list(filter(lambda x: (x[0]=='Sandra') or (x[1]=='Sandra'),G7.edges()))
G7.remove_edges_from(bridoviSandra)
for k in range(10):
    print(DSTG.random_maximal_matching(G7,[('Maja','Miroslav')]))

[('Maja', 'Miroslav'), ('Emina', 'Danijel'), ('Ana', 'Marijan')]
[('Maja', 'Miroslav'), ('Ana', 'Marijan'), ('Emina', 'Danijel')]
[('Maja', 'Miroslav'), ('Ana', 'Ivan'), ('Emina', 'Danijel'), ('Ines', 'Marijan')]
[('Maja', 'Miroslav'), ('Ines', 'Marijan'), ('Ana', 'Ivan'), ('Emina', 'Danijel')]
[('Maja', 'Miroslav'), ('Ana', 'Ivan'), ('Emina', 'Marijan')]
[('Maja', 'Miroslav'), ('Emina', 'Marijan'), ('Ana', 'Ivan')]
[('Maja', 'Miroslav'), ('Ana', 'Ivan'), ('Ines', 'Marijan'), ('Emina', 'Danijel')]
[('Maja', 'Miroslav'), ('Emina', 'Marijan'), ('Ana', 'Ivan')]
[('Maja', 'Miroslav'), ('Ines', 'Marijan'), ('Emina', 'Danijel'), ('Ana', 'Ivan')]
[('Maja', 'Miroslav'), ('Ines', 'Marijan'), ('Ana', 'Ivan'), ('Emina', 'Danijel')]

Zadatak

Nina, Danijela, Sandra, Iva, Renata, Mirela i Marija poznaju neke od mladića $M_1,\ldots,M_8$. Preciznije, Nina poznaje mladiće $M_1$, $M_2$ i $M_6$. Danijela poznaje $M_2$, $M_3$ i $M_6$. Sandra poznaje $M_1$, $M_3$ i $M_5$. Iva poznaje $M_4$, $M_7$ i $M_8$. Renata poznaje $M_1$, $M_5$ i $M_6$. Mirela poznaje $M_1$, $M_3$ i $M_6$. Marija poznaje $M_3$, $M_5$ i $M_6$.

  • Svaka od djevojaka ima veliku želju udati se za nekog od mladića kojeg poznaje. Dokažite da je to unatoč njihovim silnim željama ipak nemoguće.
  • Pronađite jedan mogući način udavanja tih djevojaka tako da čim manje djevojaka bude razočarano. Djevojka je po definiciji razočarana ako se nije uspjela udati za mladića kojeg poznaje.

Rješenje

Konstruiramo bipartitni graf. U jednoj particiji su djevojke, a u drugoj mladići. Djevojke su susjedne samo s onim mladićima koje poznaju.

In [108]:
G8=nx.Graph({"Nina":["M1","M2","M6"],"Danijela":["M2","M3","M6"],"Sandra":["M1","M3","M5"], "Iva":["M4","M7","M8"],
          "Renata":["M1","M5","M6"],"Mirela":["M1","M3","M6"],"Marija":["M3","M5","M6"]})
In [109]:
G8pos={"Nina":[0,0],"Danijela":[2,0],"Sandra":[4,0],"Iva":[6,0],"Renata":[8,0],"Mirela":[10,0],"Marija":[12,0], 
       "M1":[-0.5,3],"M2":[1.5,3],"M3":[3.5,3],"M4":[5.5,3],"M5":[7.5,3],"M6":[9.5,3],"M7":[11.5,3],"M8":[13.5,3]}
In [110]:
figure(figsize=(12,5.5))
ylim(-0.4,3.5)
nx.draw(G8,G8pos,with_labels=True,node_color='y',node_size=2800)

Nije moguće ispuniti želje svim djevojkama jer najveće sparivanje u grafu ima samo 6 elemenata, a djevojaka je ukupno 7.

In [111]:
nx.max_weight_matching(G8, maxcardinality=True)
Out[111]:
{('Danijela', 'M2'),
 ('M1', 'Renata'),
 ('M3', 'Mirela'),
 ('M5', 'Sandra'),
 ('M6', 'Nina'),
 ('M8', 'Iva')}

Kada ručno rješavamo, trebamo se pozvati na Hallov teorem.

Naime, ako uzmemo, $T\subseteq X$, $T=\{\text{Nina}, \text{Danijela}, \text{Sandra}, \text{Renata}, \text{Mirela}, \text{Marija}\}$, tada je $S(T)=\{M_1, M_2, M_3, M_5, M_6\}$. No, tada je kardinalni broj skupa $S(T)$ strogo manji od kardinalnog broja skupa $T$ pa prema Hallovom teoremu ne postoji sparivanje koje zasićuje svaki vrh iz $X$.

In [112]:
figure(figsize=(12,5.5))
DSTG.najvece_sparivanje_graf(G8,G8pos,velicina_vrha=2800,slika=[0.05,0.12])

Zadatak

Osam djevojaka su odlučile otići tjedan dana na veslanje u predivnu prirodu. Kako na tom mjestu u toj predivnoj prirodi postoje samo četiri čamca u koje stanu po dvije djevojke, one se moraju podijeliti u parove. Međutim, neke od djevojaka ne žele veslati zajedno iz nekih privatnih razloga. Sljedeća tablica nam razotkriva koje djevojke žele zajedno veslati. Ako neke dvije djevojke žele zajedno veslati, u tablici je odgovarajuće mjesto označeno s 1. Ako je neko mjesto u tablici označeno s 0, tada odgovarajuće djevojke ne žele zajedno veslati.

♦ Marija Janja Ivana Sandra Danijela Katarina Petra Dijana
Marija ♦ 0 0 0 1 1 0 1
Janja 0 ♦ 0 1 1 1 0 0
Ivana 0 0 ♦ 1 0 0 1 1
Sandra 0 1 1 ♦ 0 0 1 0
Danijela 1 1 0 0 ♦ 0 0 1
Katarina 1 1 0 0 0 ♦ 0 1
Petra 0 0 1 1 0 0 ♦ 0
Dijana 1 0 1 0 1 1 0 ♦
  • Pronađite jedan mogući način podjele djevojaka u parove za veslanje ukoliko je to moguće.
  • Kako to obično bude, na pola putovanja do te predivne prirode neke su se djevojke malo posvađale tako da su neke od njih čak odustale da zajedno budu u paru, iako je prije postojala mogućnost da zajedno veslaju. Dijana i Ivana više ne žele veslati zajedno, te isto tako Janja i Sandra. Da li je sada u ovom slučaju moguće djevojke rasporediti u parove za veslanje?

Rješenje

Konstruirat ćemo graf u kojemu će vrhovi biti djevojke, a dva vrha su spojena bridom jedino ako pripadne djevojke žele zajedno veslati. Tada u dobivenom grafu želimo naći savršeno sparivanje ukoliko ono postoji.

In [113]:
M=matrix([[0,0,0,0,1,1,0,1], [0,0,0,1,1,1,0,0], [0,0,0,1,0,0,1,1], [0,1,1,0,0,0,1,0], 
          [1,1,0,0,0,0,0,1], [1,1,0,0,0,0,0,1], [0,0,1,1,0,0,0,0], [1,0,1,0,1,1,0,0]])
In [114]:
G9=nx.from_numpy_matrix(M)
rj=dict(zip(range(8),['Marija','Janja','Ivana','Sandra','Danijela','Katarina','Petra','Dijana']))
G9=nx.relabel_nodes(G9,rj)

Uočite da G9 nije bipartitni graf jer sadrži cikluse neparnih duljina.

In [115]:
nx.is_bipartite(G9)
Out[115]:
False
In [116]:
figure(figsize=(5,5))
nx.draw_circular(G9,with_labels=True,node_color='y',node_size=2800)

Kako najveće sparivanje ima 4 brida, a graf ima 8 vrhova, to sparivanje je ujedno i savršeno sparivanje. Stoga se djevojke mogu grupirati u parove za veslanje tako da svaka djevojka vesla s nekom od djevojaka s kojom zaista želi veslati.

In [117]:
nx.max_weight_matching(G9, maxcardinality=True)
Out[117]:
{('Dijana', 'Danijela'),
 ('Ivana', 'Petra'),
 ('Janja', 'Sandra'),
 ('Marija', 'Katarina')}
In [118]:
figure(figsize=(7,7))
DSTG.najvece_sparivanje_graf(G9,nx.circular_layout(G9),velicina_vrha=2800,slika=[0.1,0.12])

No, nakon svađe situacija postaje ozbiljnija :-)

In [119]:
G9.remove_edges_from([('Dijana','Ivana'),('Janja','Sandra')])
In [120]:
figure(figsize=(5,5))
nx.draw_circular(G9,with_labels=True,node_color='y',node_size=2800)

Kako najveće sparivanje ima samo 3 brida u grafu od 8 vrhova, zaključujemo da u zadanom grafu nema savršenog sparivanja pa se u ovom slučaju djevojke ne mogu rasporediti u parove za veslanje tako da svaka djevojka vesla s nekom od djevojaka s kojom zaista želi veslati.

In [121]:
nx.max_weight_matching(G9, maxcardinality=True)
Out[121]:
{('Dijana', 'Marija'), ('Ivana', 'Petra'), ('Janja', 'Katarina')}

Jedno najveće sparivanje u kojemu su Sandra i Danijela ostale bez svojeg para pa bi bile prisiljene zajedno veslati, iako one ne žele zajedno veslati.

In [122]:
figure(figsize=(7,7))
DSTG.najvece_sparivanje_graf(G9,nx.circular_layout(G9),velicina_vrha=2800,slika=[0.1,0.12])
In [ ]: